Extreme Value Theorem
TLDRThe video script discusses the Extreme Value Theorem, emphasizing that a continuous function on a closed interval attains both a minimum and a maximum within that interval. It illustrates this with examples, highlighting the difference between absolute and relative extrema. The concept of Fermat's theorem is introduced, explaining that at points of local maximum or minimum, the derivative is zero, marking these as critical points. The video also cautions about identifying extrema in open intervals where the theorem does not apply.
Takeaways
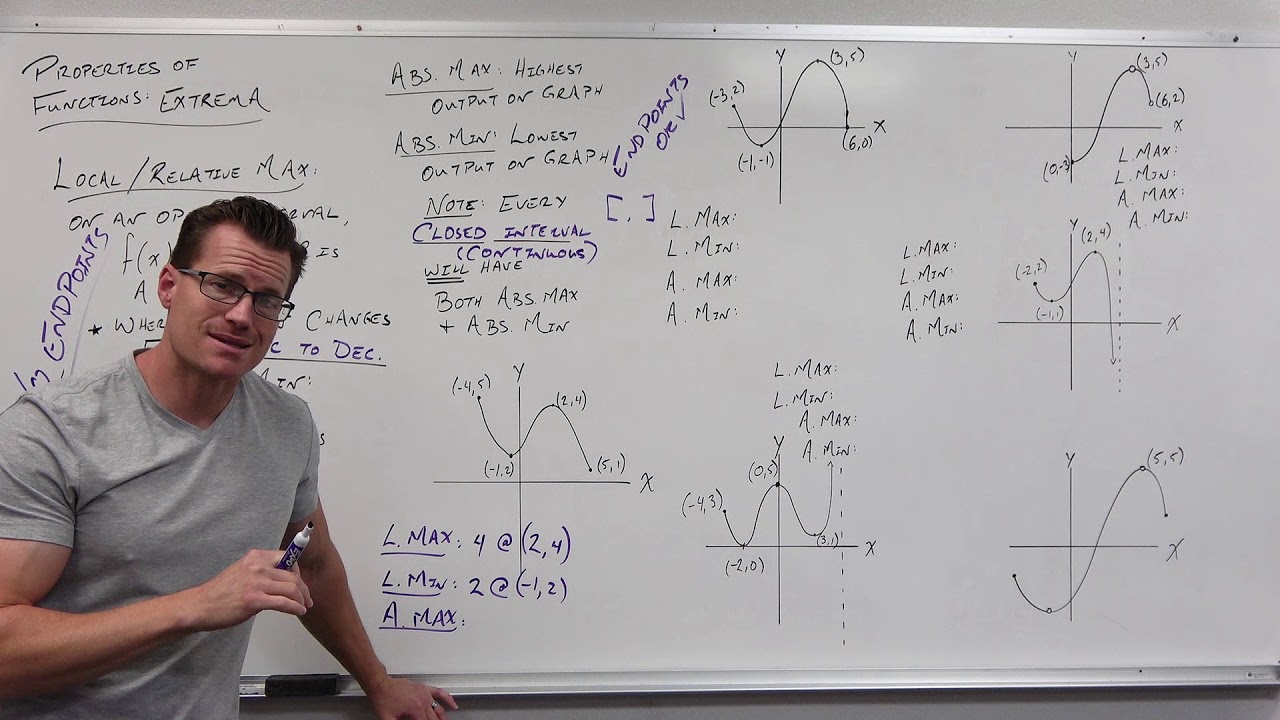
- 📌 The Extreme Value Theorem states that if a function f is continuous on a closed interval [a, b], then it has both a minimum and a maximum on that interval.
- 📈 To illustrate this, a graph with a curve must include both endpoints a and b, as these are part of the closed interval where the extrema must lie.
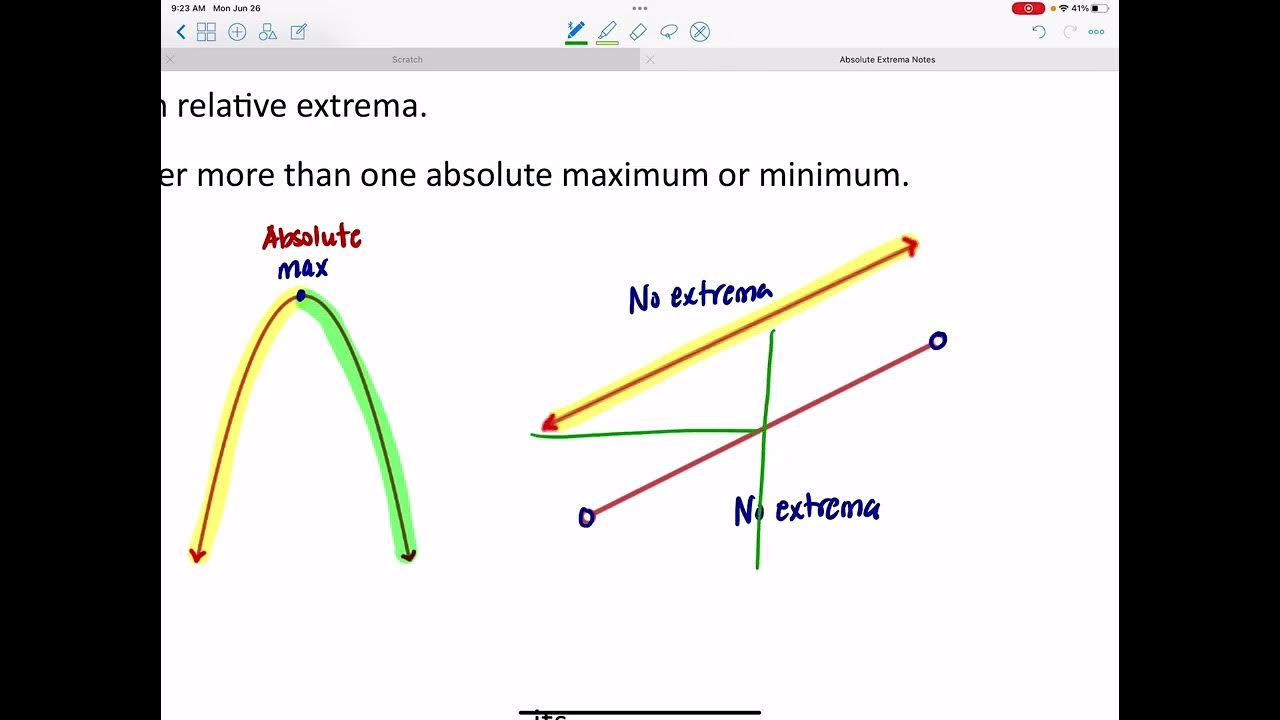
- 🔍 Identifying extrema involves locating the highest and lowest points on the graph within the specified interval, which represent the absolute maximum and minimum, respectively.
- 🔄 In graphs, points of interest beyond the absolute extrema are local (or relative) maximums and minimums, which also require attention.
- 🌟 Fermat's Theorem is introduced to explain that at points of local maximum or minimum, the derivative of the function is zero, leading to horizontal tangent lines at these points.
- 🧐 For a point to be considered a critical number, the first derivative must be zero or non-existent, as this indicates a potential local maximum or minimum.
- 📊 When analyzing graphs, it's important to distinguish between open and closed intervals, as the Extreme Value Theorem applies only to closed intervals.
- 🚫 An absolute minimum or maximum is not guaranteed in an open interval, even if the graph suggests a high or low point, as the interval does not include the actual endpoints.
- 🔍 In examples with multiple points of interest, such as points a, b, c, and d, one must carefully identify both absolute and relative extrema, as well as critical numbers.
- 💡 Understanding the concepts of open and closed intervals, as well as the implications of zero derivatives, is crucial for applying the Extreme Value and Fermat's Theorems correctly.
Q & A
What is the Extreme Value Theorem and what does it state?
-The Extreme Value Theorem is a fundamental concept in calculus which states that if a function f is continuous on a closed interval [a, b], then the function has both a minimum and a maximum value on that interval.
What is the difference between an absolute maximum and an absolute minimum?
-An absolute maximum is the highest point on the graph of a function within a given interval, while an absolute minimum is the lowest point. These points must lie within the interval, which should be closed for the theorem to apply.
What is a closed interval and how does it relate to the Extreme Value Theorem?
-A closed interval includes both of its endpoints. The Extreme Value Theorem applies to closed intervals, ensuring that a continuous function on such an interval will have both an absolute maximum and an absolute minimum.
What are local extrema and how do they relate to the graph of a function?
-Local extrema, also known as relative extrema, are points on the graph of a function where the function reaches a temporary maximum (local maximum) or minimum (local minimum). These points are not necessarily the overall highest or lowest points on the graph.
What is Fermat's Theorem and how does it connect to local extrema?
-Fermat's Theorem states that if a function f has a local maximum or minimum at a point c where the derivative exists, then the derivative of f at c is zero. This means that at points of local extrema, the function's tangent is horizontal, indicating a zero slope.
What are critical numbers and how do they relate to Fermat's Theorem?
-Critical numbers are points on the graph of a function where the derivative is zero or does not exist. These points are significant because they often correspond to local extrema, as indicated by Fermat's Theorem.
How can you identify critical numbers on a graph?
-Critical numbers can be identified by finding points on the graph where the tangent line is horizontal, which corresponds to a slope of zero. These points often represent local maxima or minima.
What is the difference between an open interval and a closed interval in terms of the Extreme Value Theorem?
-An open interval does not include its endpoints, whereas a closed interval does. The Extreme Value Theorem applies to closed intervals, ensuring the existence of absolute maxima and minima. In an open interval, these absolute extrema are not guaranteed.
Why might you not find both an absolute maximum and minimum on a graph?
-You may not find both an absolute maximum and minimum if the interval is not closed. In such cases, even if there are high and low points on the graph, they are not officially the absolute maximum or minimum according to the Extreme Value Theorem.
How can understanding the Extreme Value Theorem and Fermat's Theorem help in the study of calculus?
-Understanding these theorems helps in analyzing the behavior of functions, particularly in identifying and locating extrema. This knowledge is crucial for solving optimization problems and for gaining insights into the properties of continuous functions.
What is the significance of identifying local extrema in the study of functions?
-Identifying local extrema is important as it provides information about the function's behavior at specific points and can help in understanding the function's local maximization or minimization problems, which are common in various applications such as economics, physics, and engineering.
Outlines
📈 Extreme Value Theorem and its Applications
This paragraph introduces the Extreme Value Theorem, a fundamental concept in calculus, stating that if a function f is continuous on a closed interval [a, b], then it attains both a minimum and a maximum value within that interval. The explanation is illustrated with a graph example, highlighting the difference between endpoints and the existence of minimum and maximum points within the interval. The paragraph further elaborates on identifying extrema on graphs, differentiating between absolute extrema, which occur at the endpoints or within the interval, and relative extrema, also known as local maxima or minima. Fermat's Theorem is introduced, explaining its relevance to points with horizontal tangent lines and the concept of critical numbers, where the derivative of the function is zero or does not exist.
🔍 Identifying Extreme Values in Functions
This paragraph continues the discussion on identifying extreme values in functions, emphasizing the importance of understanding the difference between closed and open intervals. It clarifies that for an absolute minimum or maximum to exist, the interval must be closed, as exemplified by the points a and b in the provided graph. The paragraph also cautions against mistaking points with high or low values for absolute extrema if they do not lie on a closed interval. The explanation includes a visual representation of points that could be mistaken for absolute maxima or minima but are not due to the open nature of the interval. The concept of critical numbers is reiterated, reinforcing their significance in analyzing the behavior of functions.
Mindmap
Keywords
💡Extreme Value Theorem
💡Closed Interval
💡Continuous Function
💡Absolute Maximum/Minimum
💡Graph
💡Endpoint
💡Local Maximum/Minimum
💡Fermat's Theorem
💡Derivative
💡Critical Numbers
💡Open Interval
Highlights
The Extreme Value Theorem states that if a function f is continuous on a closed interval [a, b], then it has both a minimum and a maximum on that interval.
A closed interval must include its endpoints, which are represented by points a and b in the theorem's illustration.
The absolute maximum of a function on a closed interval is the highest point achievable by the function within that interval.
Similarly, the absolute minimum is the lowest point the function reaches within the specified closed interval.
When identifying extrema on a graph, it's crucial to recognize that the endpoints are part of the closed interval and thus can be minimum or maximum points.
In some cases, the absolute maximum or minimum may not be at the endpoints but still exist within the interval.
Local maxima or minima, also known as relative extrema, are points where the function reaches a high or low point that is not necessarily global.
At points of local maxima or minima, Fermat's Theorem states that the first derivative of the function is zero.
Points where the first derivative is zero are known as critical points, which are essential in identifying potential local maxima or minima.
An open interval does not guarantee the existence of an absolute maximum or minimum, as the function's behavior outside the interval is not considered.
When the graph of a function has open circles at the endpoints, it indicates an open interval, and the Extreme Value Theorem does not apply.
Even if a point appears to be the highest or lowest on a graph, it is not considered an absolute maximum or minimum if the interval is not closed.
The presence of a horizontal tangent line at a point indicates a local extremum, and the derivative at that point is zero.
Critical numbers are points where the derivative of the function is zero or does not exist, which are significant in analyzing the function's behavior.
Understanding the difference between absolute and relative extrema is crucial for correctly applying the Extreme Value Theorem and analyzing functions.
The theorem applies to continuous functions on closed intervals, and being able to identify extrema is important for solving optimization problems and understanding the behavior of functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: