Properties of Functions - Extrema (Precalculus - College Algebra 10)
TLDRThe video script provides an in-depth explanation of local or relative extrema, which are the high and low points of a graph, and absolute extrema, which are the highest and lowest points the graph can attain. It clarifies that local maxima and minima occur within an open interval where a function changes from increasing to decreasing or vice versa, and these local points are not to be confused with absolute maxima and minima, which can occur at endpoints or be the same as local extrema. The script emphasizes the importance of understanding these concepts for future calculus studies, particularly when working with derivatives and horizontal tangents. It also highlights that every closed continuous interval guarantees an absolute maximum and minimum, but local extrema are not guaranteed and can occur multiple times at different points on the graph. The video aims to give viewers a solid foundation in identifying these points on a graph, which is crucial for more advanced mathematical analysis.
Takeaways
- 📈 **Local vs. Absolute Extrema**: A local or relative maximum/minimum is a high or low point on a graph within a neighborhood or open interval, whereas an absolute maximum/minimum is the highest or lowest point on the entire graph.
- 🔍 **Identification of Local Extrema**: Look for points where the function changes from increasing to decreasing for a local maximum, and from decreasing to increasing for a local minimum.
- 📌 **Open Interval Definition**: Local maxima and minima occur within open intervals, meaning endpoints are not included in the definition of a local extremum.
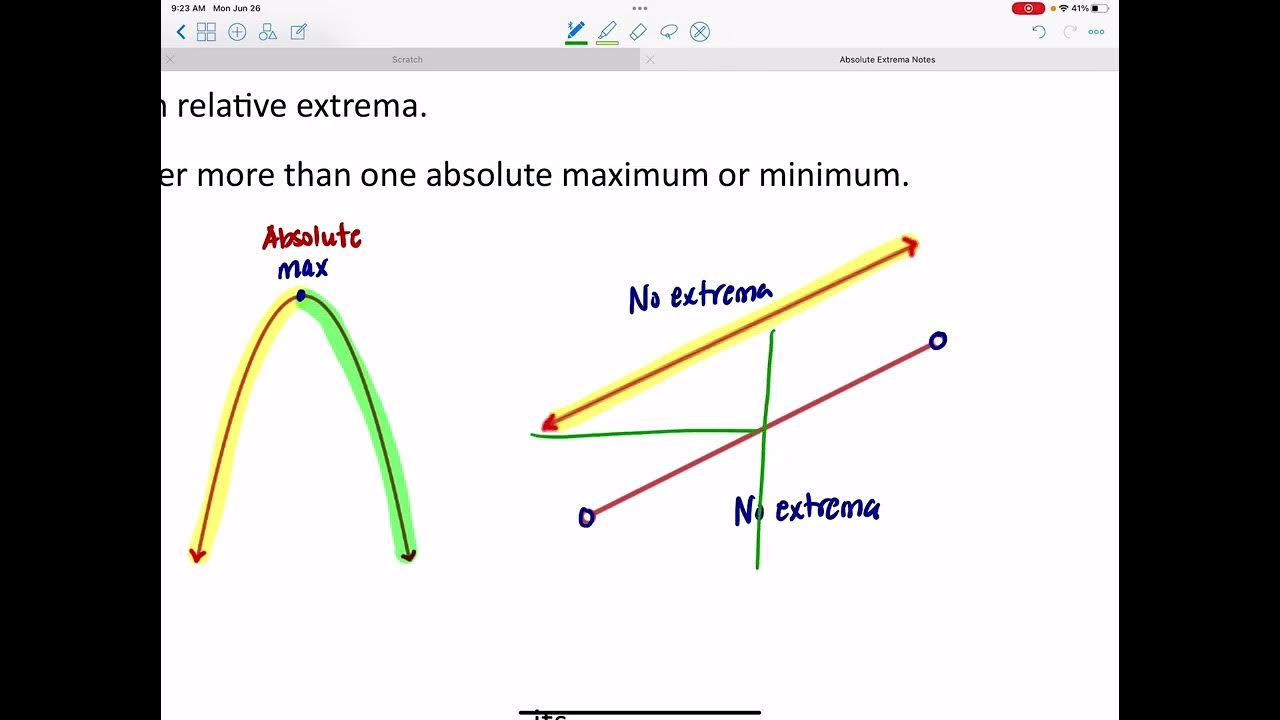
- 🏁 **Endpoints and Absolute Extrema**: Absolute maxima and minima can occur at endpoints of the graph, unlike local extrema which cannot.
- 🔺 **Multiple Extrema**: A graph can have more than one local maximum or minimum, each defined within its own open interval.
- ∞ **Continuity and Closed Intervals**: A continuous function on a closed interval guarantees the existence of an absolute maximum and minimum.
- 🚫 **Non-existence of Extrema**: If a graph is not continuous or the interval is not closed, the existence of absolute extrema is not guaranteed.
- ↗️↘️ **Changes in Function Behavior**: Local extrema generally occur where there is a change in the behavior of the function (from increasing to decreasing or vice versa).
- 📉 **No Local Extrema at Removed Points**: If a point is removed from a graph (creating a discontinuity), a local extremum cannot occur at that point.
- 🌟 **Absolute Extrema in Discontinuous Functions**: Even in discontinuous functions, absolute extrema can exist, but they will occur at endpoints or local maxima/minima if present.
- 🔄 **Infinite Values**: A graph that increases or decreases indefinitely without bound, such as approaching infinity, will not have an absolute maximum or minimum.
Q & A
What is the difference between a local maximum and a global (absolute) maximum?
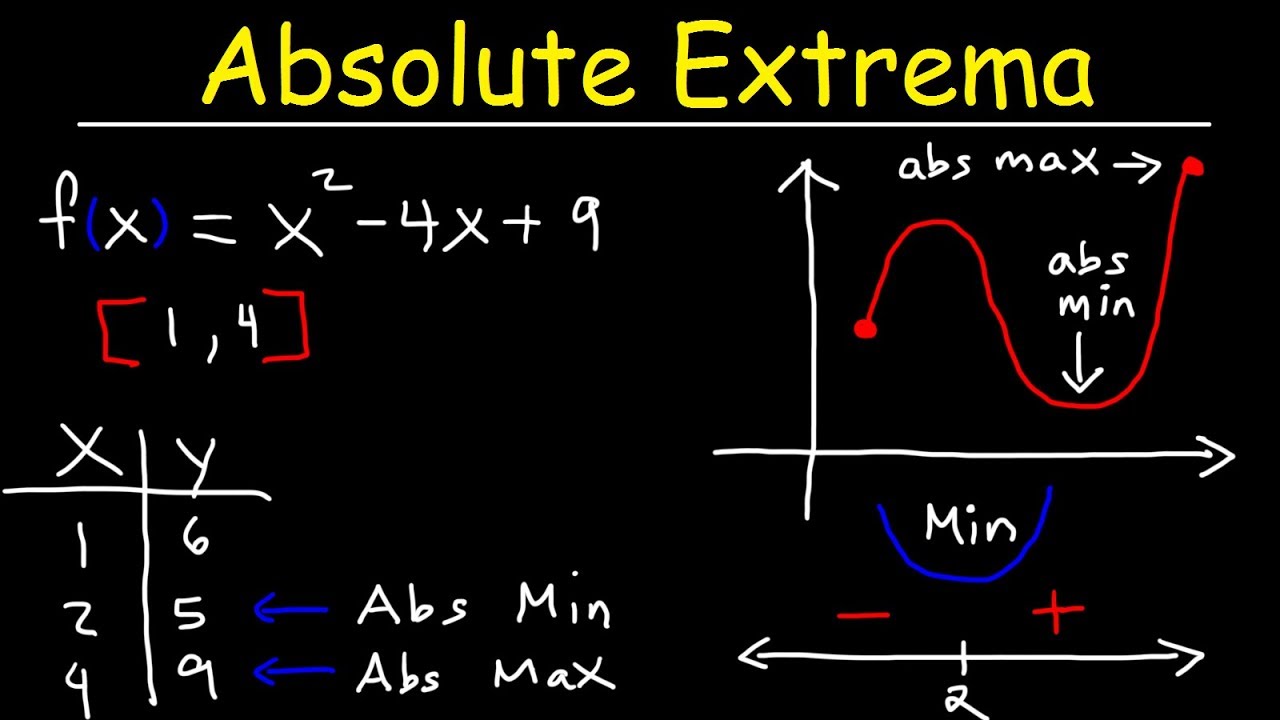
-A local maximum, also known as a relative maximum, is the highest point in a graph within a particular neighborhood or open interval. A global or absolute maximum is the highest point that the graph attains over its entire domain.
How do you identify a local maximum on a graph?
-A local maximum is generally identified where the function changes from increasing to decreasing, resulting in a peak within a neighborhood of points on the x-axis.
What is the definition of a local minimum?
-A local minimum is the lowest point in a graph within a particular neighborhood or open interval, typically identified where the function changes from decreasing to increasing, forming a trough.
Why can't local extrema occur at endpoints?
-Local extrema, which include local maxima and minima, cannot occur at endpoints because they are defined within open intervals. Endpoints are part of closed intervals and do not provide a neighborhood to compare values around the point.
What is guaranteed to exist in every closed and continuous interval of a function?
-In every closed and continuous interval, there is a guarantee of the existence of both an absolute maximum and an absolute minimum.
Can a function have more than one local maximum or minimum?
-Yes, a function can have multiple local maxima or minima as they are defined within individual neighborhoods or open intervals, which can occur at different points on the graph.
What is the significance of derivatives in finding local extrema?
-Derivatives are crucial in finding local extrema because they help identify points where the tangent to the graph is horizontal, which are potential candidates for local maxima or minima.
How does the presence of a discontinuity affect the existence of local and absolute extrema?
-A discontinuity can remove a point that could have been a local extremum. If the interval is no longer continuous, the guarantee of an absolute extremum within a closed interval is lost.
What is the difference between the output value and the point at which a local or absolute extremum occurs?
-The output value refers to the y-coordinate of the extremum, which is the value that is either a maximum or minimum. The point, on the other hand, refers to the x-coordinate where this output value occurs.
Why can an absolute maximum occur at an endpoint?
-An absolute maximum can occur at an endpoint because it is defined as the highest output value attained by the graph, and if the endpoint represents this highest value, it can be considered an absolute maximum.
What happens to the concept of local extrema when the function is not differentiable at a certain point?
-If a function is not differentiable at a certain point, traditional calculus methods for finding local extrema (which rely on derivatives) cannot be applied at that point. However, the function may still have a local extremum there based on the behavior of the function around that point.
Outlines
📈 Understanding Local and Absolute Extrema
This paragraph introduces the concepts of local or relative extrema, which are the high and low points on a graph within a certain neighborhood or open interval. It explains that a local maximum is a point where the function changes from increasing to decreasing, and a local minimum is where it changes from decreasing to increasing. The paragraph also differentiates between local extrema and absolute extrema, noting that the latter represents the highest or lowest point on the entire graph. The importance of understanding these concepts is emphasized for future calculus studies involving derivatives and horizontal tangents.
📐 Characteristics of Local and Absolute Extrema
The second paragraph delves into the properties of local and absolute extrema. It clarifies that every closed and continuous interval guarantees the existence of an absolute maximum and minimum. However, local extrema cannot occur at endpoints since they are defined within open intervals. The paragraph also discusses the possibility of having multiple local extrema at the same value and the conditions under which absolute extrema can occur at endpoints or coincide with local extrema.
🔍 Identifying Local and Absolute Extrema on Graphs
This paragraph provides a method for identifying local and absolute extrema on a graph. It explains that for a continuous function on a closed interval, one can expect both local and absolute extrema. The process involves looking for changes in the direction of the function's increase or decrease to find local extrema. Absolute extrema are determined by comparing the highest and lowest output values of the function, which could occur at local extrema or endpoints. The importance of differentiating between local and absolute extrema, especially in non-closed intervals, is highlighted.
🚫 Discontinuities and Their Impact on Extrema
The fourth paragraph discusses the impact of discontinuities on the existence of local and absolute extrema. It explains that if a point is removed from a graph, creating a discontinuity, neither local nor absolute extrema can exist at that point. The paragraph emphasizes that for a local extremum to exist, there must be a change in direction within an open interval, which is not possible if the point is missing. Similarly, an absolute extremum requires an actual highest or lowest value on the graph, which cannot be guaranteed without a closed and continuous interval.
∞ Multiple Local Extrema and Their Behavior
This paragraph explores the possibility of having multiple local maxima and minima on a graph. It explains that multiple local extrema can occur because they are defined within individual open intervals. The paragraph also addresses the behavior of functions that have an infinite number of local extrema, such as sine and cosine functions, which can have peaks and troughs repeating at regular intervals. It concludes by emphasizing that while there can be many local extrema, there can only be one absolute maximum and minimum on a continuous curve on a closed interval.
🔢 Absolute Extrema and Their Multiple Occurrences
The final paragraph focuses on absolute extrema, noting that they can occur at more than one point if the highest or lowest output value is attained at multiple x-values. It reinforces the concept that an absolute maximum or minimum is the highest or lowest output value on the entire graph, which can be found at local maxima, local minima, or endpoints. The paragraph also clarifies that while local extrema are based on open intervals and cannot include endpoints, absolute extrema consider the entire graph, including endpoints.
Mindmap
Keywords
💡Local Maximum
💡Local Minimum
💡Absolute Maximum
💡Absolute Minimum
💡Open Interval
💡Derivative
💡Endpoint
💡Continuous Function
💡Increasing/Decreasing
💡Tangent
💡Asymptote
Highlights
Explains the concept of local or relative extrema, including local maxima and minima, and absolute maxima and minima.
Differentiates between local maxima, which are high points in a graph within an open interval, and absolute maxima, which are the highest points on the entire graph.
Discusses that local maxima and minima occur where the function changes from increasing to decreasing or vice versa.
Clarifies that the output value at a certain x value is what defines a local or absolute extremum, not the point itself.
Notes that local or relative extrema cannot occur at endpoints, while absolute extrema can.
Mentions that every closed and continuous interval guarantees an absolute maximum and minimum.
Explains that absolute maxima and minima occur at local maxima, minima, or endpoints on continuous differentiable curves.
Demonstrates how to identify local and absolute extrema through graph analysis, emphasizing the importance of understanding changes in the function's behavior.
Provides examples to illustrate the concepts, including cases where local maxima and minima do not exist due to missing points in the graph.
Stresses the importance of looking for areas in the graph where the function's behavior changes from increasing to decreasing for local maxima and vice versa for minima.
Discusses the possibility of having multiple local maxima and minima within a graph, each defined within their own open interval.
Points out that absolute maxima and minima can occur at more than one x-value if the highest or lowest output is attained at multiple points.
Uses calculus concepts such as derivatives and horizontal tangents to further explain how to determine local maxima and minima algebraically.
Highlights the difference between open intervals, where local extrema are defined, and closed intervals, which include endpoints where absolute extrema can occur.
Explains that the presence of asymptotes or discontinuities in a graph can affect the existence of local and absolute extrema.
Concludes by emphasizing the practical applications of understanding extrema in calculus for analyzing the behavior of functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: