Absolute Extrema

Stacy Colaiacovo

26 Jun 202332:11

EducationalLearning

32 Likes 10 Comments

TLDRThis lesson delves into the concepts of absolute and relative extrema, contrasting them and explaining their relationship to open and closed intervals. The instructor clarifies that while relative extrema can occur at turning points within an interval, absolute extrema, which are the highest or lowest points on a graph, can only be one each and may coincide with relative extrema. The lesson emphasizes the importance of the extreme value theorem, which states that a continuous function on a closed interval must have an absolute maximum and minimum. The process for finding these extrema involves finding critical points through derivatives, evaluating the function at endpoints, and comparing outputs to determine the absolute maximum and minimum. The instructor uses various functions and intervals to illustrate the algebraic process and confirms the results with graphing, providing a comprehensive understanding of the topic.

Takeaways

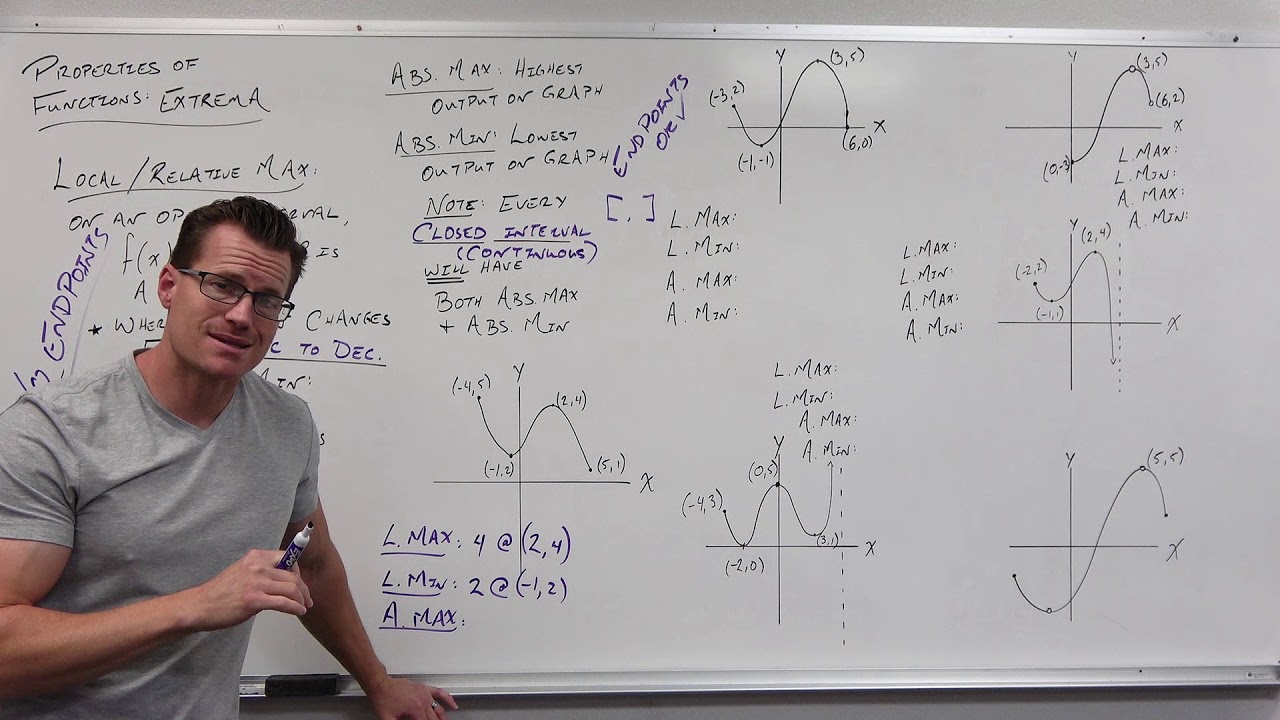
📈 The concept of absolute extrema refers to the highest (absolute maximum) or lowest (absolute minimum) points on a graph within a given interval.
🔍 Relative extrema, or local maxima and minima, are points that are the highest or lowest within a certain neighborhood but not necessarily the overall highest or lowest.
➡️ Open intervals do not include their endpoints and may not have any extrema, especially if the graph extends indefinitely in either direction.
🔄 Turning points on a graph, where the function changes from increasing to decreasing or vice versa, are potential locations for relative extrema.
📊 The absolute maximum and minimum are specific types of extrema that are the highest and lowest points on the graph, respectively, and they cannot be exceeded by any other points.
🔗 Absolute extrema often coincide with relative extrema, but it's possible to have multiple relative extrema while there can only be one absolute maximum and one absolute minimum.
📐 On a closed interval, which includes its endpoints, the extreme value theorem states that a continuous function must have an absolute maximum and an absolute minimum.
🔢 To find the absolute extrema algebraically, calculate the function values at critical points (where the derivative is zero or undefined) and endpoints of the interval, then compare to find the highest and lowest values.
📉 For linear functions or constant intervals, there are no turning points and thus no extrema if the interval is open; however, if the interval is closed, extrema will occur at the endpoints.
🧮 The process of finding derivatives is crucial for locating relative extrema, which can then be evaluated to determine if they are also absolute extrema.
📋 The algebraic approach involves finding the first derivative, identifying critical numbers, evaluating the function at these points and endpoints, and comparing the outputs to determine the absolute extrema.

Q & A

What is the difference between an open interval and a closed interval?
-An open interval is a portion of a graph that does not include its endpoints, which could extend to positive or negative infinity. A closed interval includes its endpoints, indicating a specific start and stop location on the graph.
What are extrema and how do they relate to turning points on a graph?
-Extrema refer to the maximum and minimum points on a graph. These points often occur at turning points, where the graph transitions from increasing to decreasing or vice versa.
How is an absolute maximum different from a relative maximum?
-An absolute maximum is the highest point on the entire graph, with no point higher than it. A relative maximum, on the other hand, is a high point within a certain interval but not necessarily the highest point on the entire graph.
What is the relationship between absolute extrema and relative extrema on a graph?
-Absolute extrema are the highest and lowest points on a graph, while relative extrema are the highest and lowest points within a specific interval. They often coincide, meaning an absolute maximum can also be a relative maximum, and vice versa.
Can a function have more than one absolute maximum or minimum?
-No, a function can never have more than one absolute maximum or minimum. There can only be one highest and one lowest point on the entire graph.
What is the Extreme Value Theorem and how does it apply to closed intervals?
-The Extreme Value Theorem states that if a function is continuous on a closed interval, it must have an absolute maximum and an absolute minimum on that interval. This is a fundamental theorem in calculus with many practical applications.
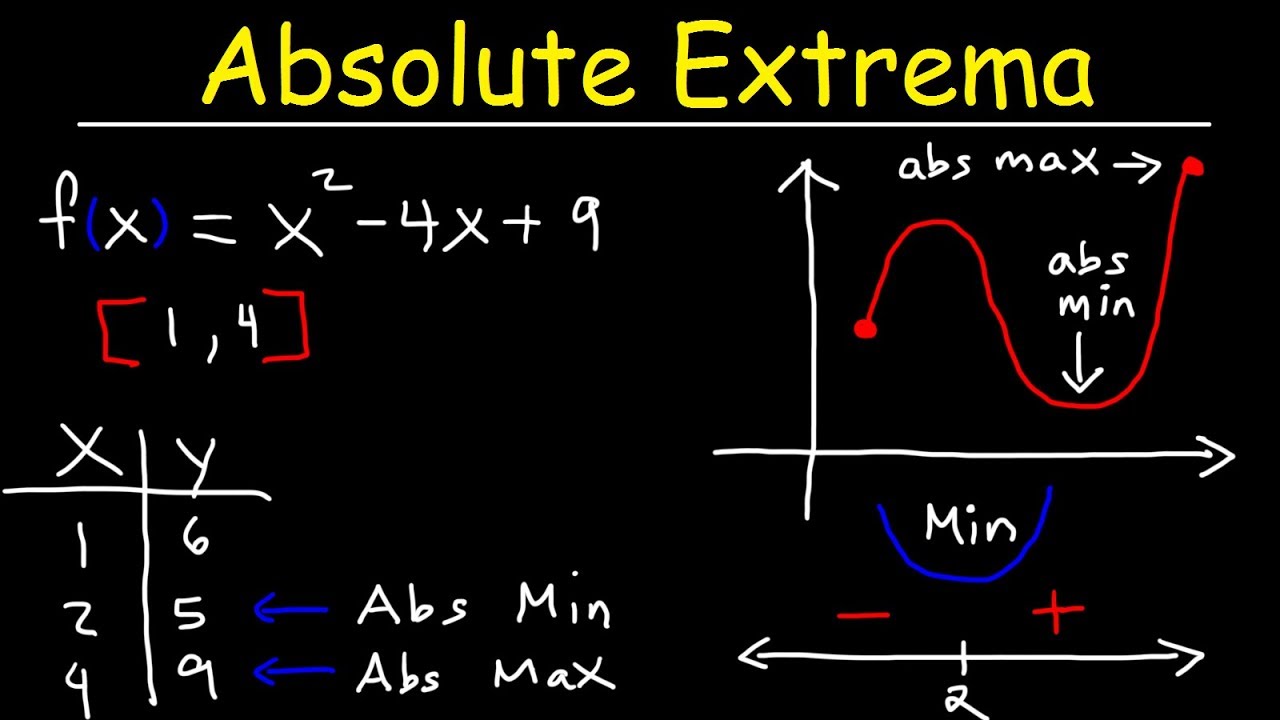
How do you algebraically find the absolute extrema of a function on a closed interval?
-To find the absolute extrema algebraically, you first find the critical numbers of the first derivative, which indicate turning points. Then, evaluate the function at these critical numbers and at the endpoints of the interval. The largest output is the absolute maximum, and the smallest output is the absolute minimum.
What is the significance of finding the first derivative of a function when looking for extrema?
-The first derivative of a function indicates the slope of the tangent to the graph at a given point. Critical numbers of the first derivative (where the derivative is zero or undefined) correspond to turning points, which are potential locations for relative or absolute extrema.
How does the process of finding absolute extrema differ when the interval is open versus when it is closed?
-On an open interval, the endpoints are not included, so the function may not have any extrema if it continues indefinitely in the direction of the interval. On a closed interval, the endpoints are included, and by the Extreme Value Theorem, the function must have both an absolute maximum and minimum within the interval.
What are the possible locations for absolute extrema on a closed interval?
-On a closed interval, absolute extrema can occur at the endpoints of the interval or at any relative extrema (turning points) that lie within the interval.
Why is it not possible to have an absolute maximum or minimum on a linear function that goes to infinity in both directions?
-A linear function that extends to positive or negative infinity does not have an absolute maximum or minimum because there is always a point higher or lower on the graph as it continues indefinitely without bound.

Outlines

00:00

📈 Introduction to Absolute and Relative Extrema

The video begins by introducing the concept of absolute extrema, contrasting it with relative extrema. It explains open and closed intervals, emphasizing that open intervals might not have extrema, while closed intervals always have an absolute maximum and minimum due to the extreme value theorem. The difference between relative maxima/minima and absolute maxima/minima is also clarified, with examples illustrating the concepts.

05:01

🔍 Identifying Relative and Absolute Extrema on Graphs

This paragraph delves into identifying relative and absolute extrema on graphs. It demonstrates how to distinguish between maximum and minimum points and how these can be either relative or absolute based on the graph's behavior. The video uses examples to show that a graph with no limits will only have relative extrema, while a graph with limits can have absolute extrema at turning points or endpoints.

10:01

🧮 Algebraic Approach to Finding Absolute Extrema

The script outlines an algebraic method for finding absolute extrema on a closed interval. It explains the process of finding critical numbers by setting the first derivative equal to zero and considering the function's values at endpoints. The importance of evaluating the function at these critical points and endpoints to determine the absolute maximum and minimum is highlighted.

15:03

📉 Example: Finding Absolute Extrema of a Quadratic Function

A quadratic function is used as an example to demonstrate the process of finding absolute extrema algebraically. The video shows how to find the first derivative, identify critical numbers, and evaluate the function at these points and the endpoints of the interval. It concludes with the algebraic results that match the graph's visual representation, confirming the location of the absolute maximum and minimum.

20:04

🤔 Confirming Results with Graphing Tools

The paragraph emphasizes the utility of graphing tools like Desmos to confirm algebraic findings. It shows how to input functions and set intervals to visualize the graph and verify the locations of maxima and minima. The video reassures that while graphs provide an easy way to identify extrema, the algebraic work complements this by providing precise values.

25:07

🔢 Calculating Absolute Extrema with Differentiation Techniques

The video concludes with a discussion on using various differentiation techniques, such as the quotient rule and product rule, to find derivatives and subsequently the absolute extrema. It demonstrates how to handle different forms of derivatives and when to consider endpoints as the only possible locations for extrema. The video reinforces the process of evaluating the function at critical numbers and endpoints to determine the absolute maximum and minimum.

30:09

📚 Summary and Encouragement for Further Practice

The final paragraph summarizes the key points covered in the video, reminding viewers of the methods to find derivatives and absolute extrema. It acknowledges the potential complexity of calculus involved in these processes but reassures that identifying maxima and minima is straightforward. The video encourages viewers to practice and reach out for help if needed, signaling the end of the lesson.

Mindmap

Keywords

💡Absolute extrema

Absolute extrema refer to the highest (absolute maximum) or lowest (absolute minimum) points on a graph of a function. In the context of the video, it is the largest or smallest value that a function can attain over its entire domain. The concept is crucial as it helps in understanding the behavior of functions, especially when considering closed intervals where the endpoints are included.

💡Relative extrema

Relative extrema, also known as local maxima or minima, are points on a graph where the function transitions from increasing to decreasing (local maximum) or decreasing to increasing (local minimum). Unlike absolute extrema, they do not have to be the highest or lowest points on the entire graph but are significant within a certain neighborhood or interval.

💡Open intervals

An open interval is a subset of the real numbers that does not include its endpoints. It is represented by parentheses in mathematical notation. In the video, it is mentioned that on an open interval, a function may or may not have any extrema, particularly if the interval extends to positive or negative infinity.

💡Closed intervals

A closed interval includes its endpoints and is represented by square brackets in mathematical notation. The video explains that for a continuous function on a closed interval, there must exist an absolute maximum and an absolute minimum due to the extreme value theorem, which is a fundamental concept in calculus.

💡Turning points

Turning points are the points on a graph where the function changes direction, either from increasing to decreasing or vice versa. These are significant as they often coincide with relative extrema. The video discusses how to identify turning points by looking for changes in the slope of the tangent to the graph.

💡Critical numbers

Critical numbers are the values of the independent variable (usually x) for which the derivative of the function is either zero or undefined. They are important for identifying potential relative or absolute extrema. In the video, finding critical numbers is a key step in determining the extrema of a function on a given interval.

💡Derivatives

Derivatives represent the rate of change of a function with respect to its variable. In the context of the video, finding the first derivative of a function is essential for locating critical numbers and potential extrema. The process of differentiating functions using various rules, such as the power rule, product rule, and quotient rule, is demonstrated.

💡Continuous function

A continuous function is one that has no breaks or gaps in its graph. The concept of continuity is important when discussing the existence of absolute extrema on a closed interval, as guaranteed by the extreme value theorem. The video emphasizes that for a function to have an absolute maximum and minimum on a closed interval, it must be continuous.

💡Extreme value theorem

The extreme value theorem states that if a function is continuous on a closed interval, then it must attain an absolute maximum and an absolute minimum on that interval. This theorem is a fundamental principle in calculus and is used in the video to explain why absolute extrema must exist under certain conditions.

💡Linear function

A linear function is a function of the form f(x) = mx + b, where m and b are constants, and m is the slope of the line. In the video, it is mentioned that a linear function that extends to positive or negative infinity does not have an absolute maximum or minimum, as there will always be points higher or lower on the graph.

💡Quotient rule

The quotient rule is a method used to find the derivative of a function that is the quotient of two other functions. It states that the derivative of the quotient of f(x) and g(x) is (f'(x)g(x) - f(x)g'(x)) / (g(x))^2. The video demonstrates the application of the quotient rule in finding the derivative of a function to locate its extrema.

Highlights

Introduction to absolute extrema and comparison with relative extrema.

Explanation of open and closed intervals and their relation to extrema.

Absolute extrema defined as the highest or lowest points on a graph.

Relative extrema as local maxima or minima that are not the absolute highest or lowest.

Absolute extrema can coincide with relative extrema under certain conditions.

Distinction between absolute and relative extrema on open intervals.

The possibility of having multiple relative extrema but only one absolute extremum.

The absence of absolute extrema on graphs that extend to infinity.

Identification of extrema by analyzing the graph's turning points.

The extreme value theorem stating that a continuous function on a closed interval must have an absolute maximum and minimum.

Algebraic method to find absolute extrema by evaluating the function at critical numbers and endpoints.

Demonstration of finding absolute extrema for a quadratic function on a specified interval.

Use of the first derivative to find turning points and critical numbers.

Differentiating various functions using power, chain, and product rules.

Process of evaluating function values at critical points and endpoints to determine absolute extrema.

Verification of algebraic solutions with graphical representation using a tool like Desmos.

Different ways to express the results of absolute extrema in terms of points, values, or within the context of the function.

Emphasis on the importance of understanding both the graphical and algebraic methods for finding extrema.

Encouragement to practice and seek help if needed for a deeper understanding of the concepts.

Transcripts

Browse More Related Video

Properties of Functions - Extrema (Precalculus - College Algebra 10)

Finding Absolute Extrema

Extreme Value Theorem

Calculus AB/BC – 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points

Extrema on an Interval

Finding Absolute Maximum and Minimum Values - Absolute Extrema

Related Tags

Absolute Extrema Relative Extrema Calculus Turning Points Open Intervals Closed Intervals Function Analysis Mathematics Graph Analysis Derivatives Extreme Value Theorem