Calculus AB/BC – 5.2 Extreme Value Theorem, Global Versus Local Extrema, and Critical Points
TLDRIn this informative transcript, Mr. Bean discusses the concept of critical points and extrema in calculus. He explains the Extreme Value Theorem, which states that a continuous function over an interval must have at least one minimum and one maximum. He differentiates between global (absolute) and local (relative) extrema, and addresses the controversy surrounding the classification of certain points as relative maxima. The transcript also covers how to identify critical points by examining where the derivative is zero or does not exist, which may indicate potential extrema. The examples provided illustrate these concepts and the process of finding critical points.
Takeaways
- 📚 The Extreme Value Theorem states that a continuous function on an interval must have at least one minimum and one maximum.
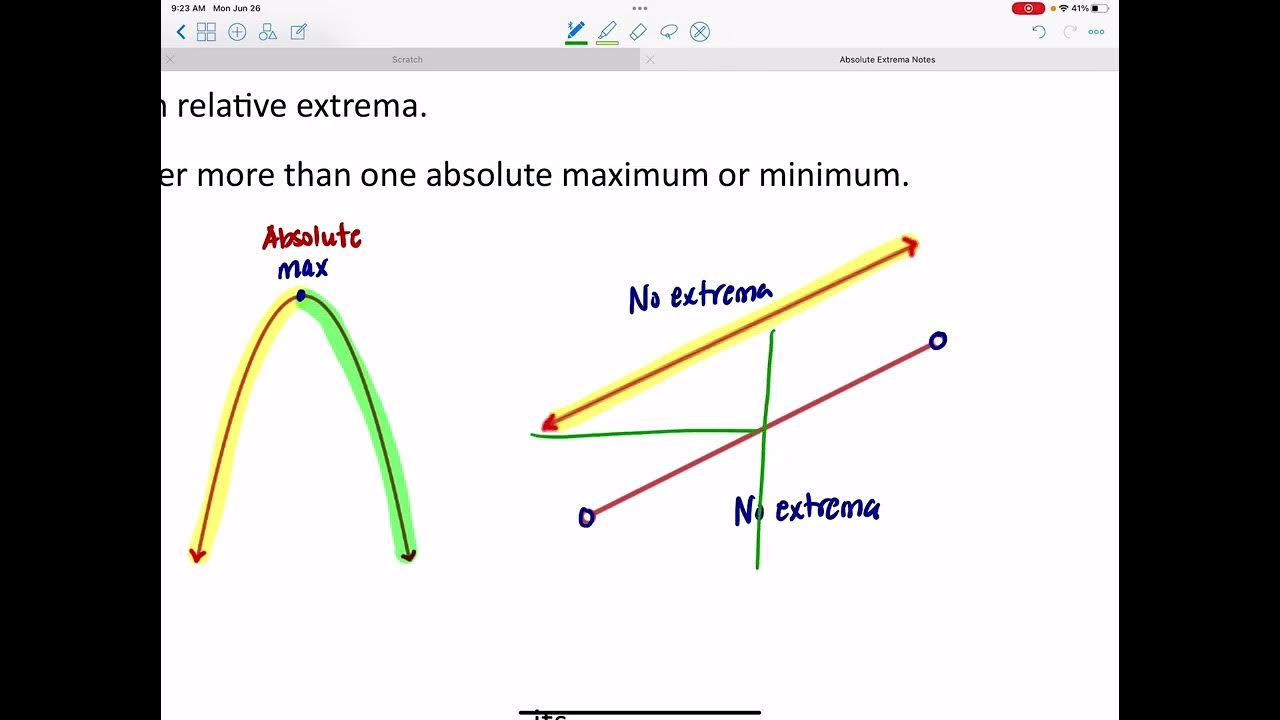
- 📈 In a graph, maximum and minimum points can be absolute or relative. Absolute extrema are the highest or lowest points on the entire graph, while relative extrema are the highest or lowest within a specific local area.
- 🔍 To identify a relative maximum or minimum, construct an open interval around the point and compare the function values within that interval.
- 🏞️ The point of a jump in a function can be a relative minimum but not an absolute maximum due to the lack of points on one side of the interval.
- 🤔 There is mathematical controversy over whether certain points, like those at the endpoints of a domain, can be considered relative extrema.
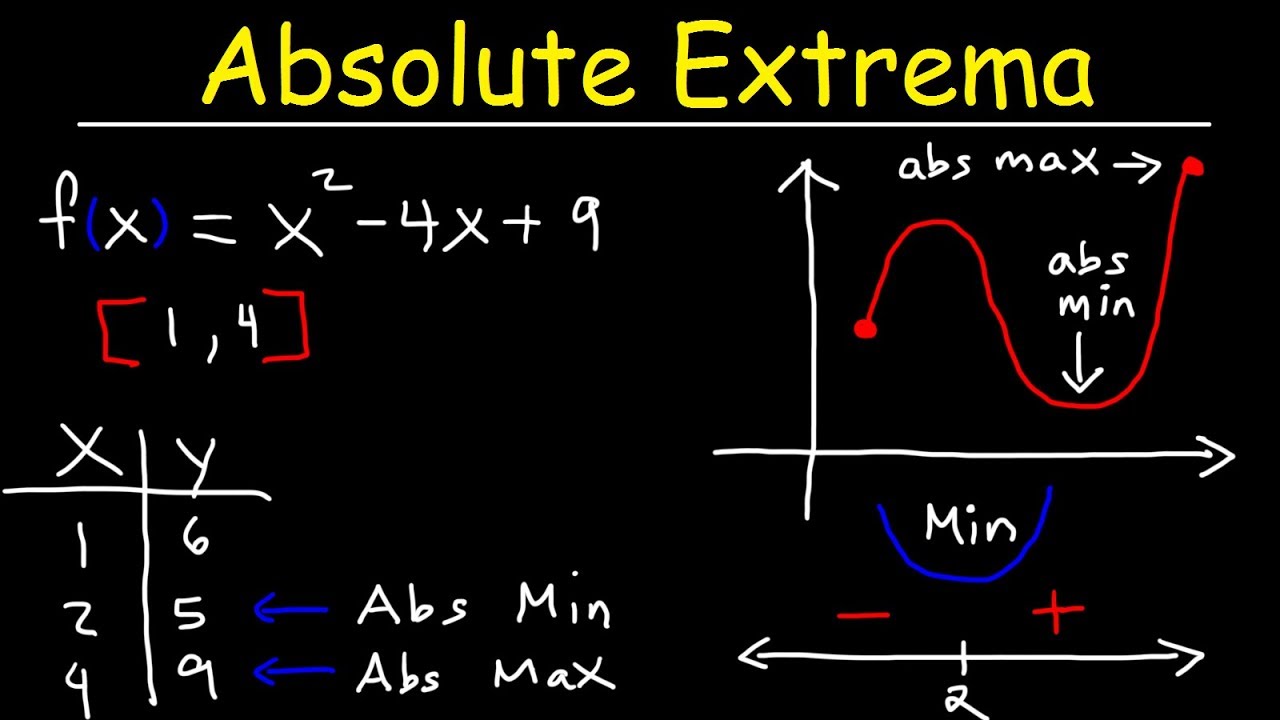
- 📝 When labeling a graph, note absolute minima and maxima with their function values and the corresponding x-values.
- 🌟 Critical points are points on a graph where the function may have an extremum. These are points where the derivative is zero or does not exist.
- 🛠️ To find critical points, take the derivative of the function and solve for when it equals zero or does not exist. These points are candidates for maxima or minima.
- 📊 For a cubic function, critical points often correspond to the function's maximum and minimum values.
- ⚠️ Be cautious when considering points where the derivative does not exist; if these points are not in the domain of the function, they are not valid critical points.
- 📂 In summary, understanding critical points and extrema is crucial for analyzing the behavior of functions and their graphs.
Q & A
What is the Extreme Value Theorem mentioned in the transcript?
-The Extreme Value Theorem states that if you have a function that is continuous over an interval from a to b, it must have at least one minimum and one maximum within that interval.
How does the transcript explain the difference between global and local extrema?
-The transcript explains that global (or absolute) extrema refer to the highest or lowest points of a function over the entire domain, whereas local (or relative) extrema refer to the highest or lowest points of a function within a specific neighborhood or interval.
What is the significance of the open circle and dot on a graph as described in the transcript?
-An open circle on a graph indicates a point that is not considered a maximum or minimum, as it is part of the function's domain but does not meet the criteria for being an extremum. A dot indicates a point that is an extremum, either a maximum or a minimum.
How does the transcript address the controversy surrounding certain points being considered relative extrema?
-The transcript acknowledges that there is disagreement among mathematicians about whether certain points, especially at the endpoints of a function's domain, should be considered relative extrema. It advises students to check with their teachers for their preferred approach and understanding of such cases.
What is the role of the derivative in identifying critical points as explained in the transcript?
-The derivative plays a crucial role in identifying critical points. A critical point can be a potential maximum or minimum if the first derivative either equals zero or does not exist at that point. Critical points are potential candidates for being extrema but do not guarantee that they are extrema.
How does the transcript describe the process of finding critical points?
-To find critical points, one must first determine the derivative of the function. Then, identify any points where the derivative is either zero or does not exist. These points are the critical points and are potential locations for local maxima or minima.
What is the importance of understanding critical points in calculus?
-Understanding critical points is important because they help in identifying the locations on a graph where the function's behavior changes, such as at local maxima or minima. This is crucial for analyzing the function's overall performance and for solving optimization problems.
What is the role of the chain rule in the second example provided in the transcript?
-In the second example, the chain rule is used to find the derivative of a composite function. It allows for the differentiation of the inner function first, which in this case is the square root of 4 minus x squared, before applying the derivative of the outer function.
How does the transcript handle the points where the derivative does not exist due to a zero denominator?
-The transcript clarifies that points where the derivative does not exist due to a zero denominator are not considered critical points if they cause the original function to be undefined. Such points are excluded from consideration as they are not within the domain of the function.
What is the final advice given in the transcript regarding the identification and labeling of extrema on a graph?
-The final advice is to always label absolute minima and maxima with certainty, as their identification is clear. However, for endpoints that might be relative extrema, students should consult with their teachers to understand the expected approach and avoid stressing over these points.
What is the significance of the jump function in the graph as discussed in the transcript?
-The jump function in the graph is significant because it cannot be an absolute extremum since there are already identified absolute minimum and maximum points. However, it can represent a relative minimum within its local interval, highlighting the importance of considering the local context when identifying extrema.
Outlines
📚 Introduction to Critical Points and Extrema
This paragraph introduces the concepts of critical points and extrema, such as maximum and minimum values, in the context of calculus. Mr. Bean explains the Extreme Value Theorem, which states that a continuous function over an interval must have at least one minimum and one maximum. The explanation includes a graphical representation to illustrate the theorem. The paragraph also distinguishes between global (absolute) and local (relative) extrema, setting the stage for a deeper understanding of these concepts in future discussions.
📈 Identifying Absolute and Relative Extrema
This paragraph delves into the specifics of identifying absolute and relative extrema on a graph. It explains how to determine if a point is an absolute minimum or maximum by comparing it with other points on the graph. The paragraph also addresses the nuances of identifying relative extrema, especially at points where the function's domain is interrupted, such as jump functions. The discussion highlights the ongoing debate among mathematicians about the classification of certain points as relative extrema, emphasizing the importance of checking with one's teacher for the preferred approach.
🔍 Locating Critical Points and Their Significance
The focus of this paragraph is on locating critical points, which are potential candidates for being extrema. It explains that critical points occur where the first derivative is either zero or does not exist. The paragraph provides a clear methodology for finding these points by examining the first derivative of a function and identifying where it equals zero or is undefined. Two examples are worked out to demonstrate this process, reinforcing the concept that while critical points indicate potential extrema, they do not confirm the presence of a maximum or minimum without further analysis.
Mindmap
Keywords
💡Critical Points
💡Extrema
💡Global and Local Extrema
💡Derivative
💡Horizontal Tangent Line
💡Endpoint
💡Open Interval
💡Absolute Maximum and Minimum
💡Relative Maximum and Minimum
💡Discontinuity
💡Chain Rule
Highlights
Introduction to critical points and extrema such as maxima and minima.
Explanation of the Extreme Value Theorem, stating that a continuous function over an interval must have at least one minimum and one maximum.
Illustration of a function graph to demonstrate the presence of multiple maxima and minima.
Discussion on the difference between global and local extrema, and the synonymous terms absolute and relative extrema.
Identification of absolute minimum and maximum on a graph with clear examples.
Explanation of relative minimum and maximum, using the concept of open intervals.
Addressing the controversy among mathematicians regarding certain types of relative maxima.
Guidance on how to label different types of extrema on a graph with specific values.
Introduction to critical points as potential locations for maxima or minima.
Explanation that a critical point can be a point where the derivative is zero or does not exist.
Process of finding critical points by setting the first derivative equal to zero.
Example of finding critical points for a cubic function, highlighting the potential for maximum and minimum values.
Discussion on the importance of considering the domain of a function when finding critical points.
Demonstration of taking the derivative of a function and analyzing it to find critical points.
Conclusion and summary of the main points covered in the lesson.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: