Extrema on an Interval
TLDRThis educational video script delves into the concept of derivatives, explaining their role in identifying extrema on a graph. It distinguishes between absolute and relative extrema, and introduces critical points where derivatives are zero or undefined. The Extreme Value Theorem (EVT) is highlighted, asserting the existence of absolute maxima and minima for continuous functions on a closed interval. The script guides viewers through finding critical numbers and using the 'candidates test' to determine the function's maximum and minimum values at specific points, illustrated with several examples including a trigonometric function.
Takeaways
- 📈 Derivatives are used to analyze the behavior of functions, particularly to find extrema (maximum and minimum points).
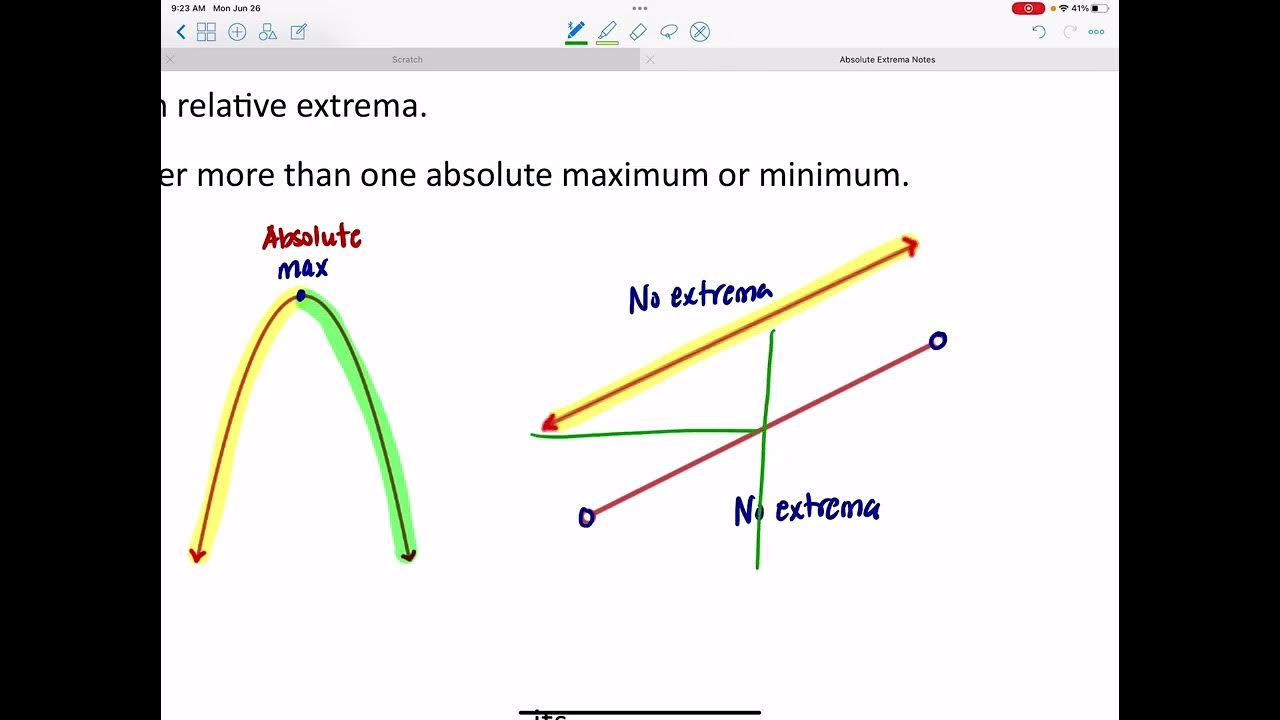
- 🔍 Absolute extrema refer to the highest or lowest points on a graph within a given interval, while relative extrema are points where the graph changes direction (from increasing to decreasing or vice versa).
- 📚 Critical numbers, also known as critical points, are values of x where the derivative is either zero or undefined. These are potential locations for extrema.
- 🔑 A theorem states that relative extrema can only occur at critical numbers, making them crucial for identifying extrema.
- 📉 The Extreme Value Theorem (EVT) asserts that if a function is continuous on an interval, it must have both an absolute maximum and an absolute minimum within that interval.
- 🔍 To find extrema, first find critical numbers by setting the derivative equal to zero or identifying where it is undefined.
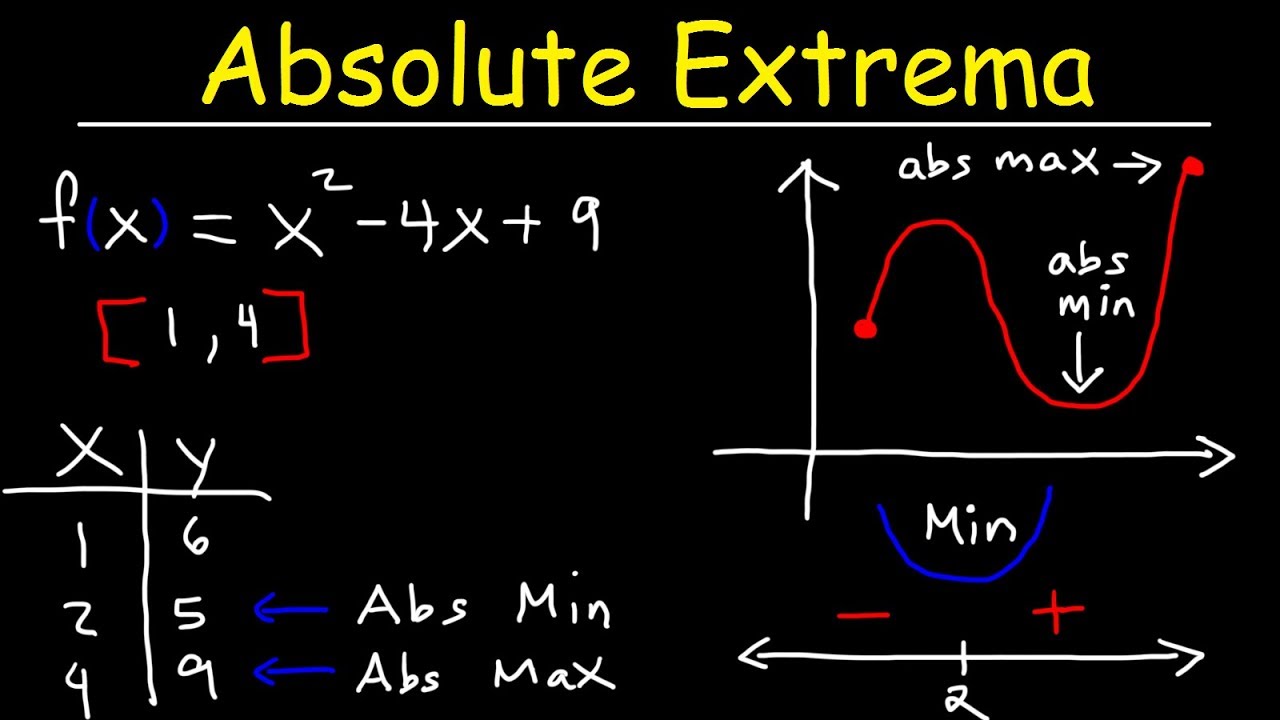
- 📊 The 'candidates test' involves evaluating the function at critical points and endpoints to determine the actual extrema.
- 🧩 The script provides examples of finding extrema for functions, demonstrating the process of taking derivatives, finding critical points, and applying the candidates test.
- 📚 The script emphasizes the importance of continuity for the EVT to hold, meaning that a function must be continuous to guarantee the existence of absolute extrema.
- 🔎 The script also highlights that the maximum or minimum of a function on an interval can only be determined if the function is continuous and reaches those values.
- 🌐 The examples include functions with different types of derivatives, such as polynomial and trigonometric functions, illustrating the generality of the methods discussed.
Q & A
What are derivatives used for in the context of the video script?
-Derivatives are used to analyze the behavior of a function, particularly to find out where the function has its maximum and minimum values, which are important for understanding extrema.
What is the difference between an absolute extrema and a relative extrema as explained in the script?
-An absolute extrema refers to the highest or lowest point on a graph within a given interval, while a relative extrema is where the graph changes direction, either from increasing to decreasing or vice versa.
What is a critical number or critical point in the context of calculus?
-A critical number or critical point is a value of x where the derivative of a function is either zero or undefined. These points are important because they are potential locations for relative extrema.
What is the significance of the theorem mentioned in the script regarding relative extrema and critical numbers?
-The theorem states that relative extrema can only occur at critical numbers. This is significant because it provides a method to identify potential locations of extrema by looking for critical points.
What is the Extreme Value Theorem (EVT) and why is it important?
-The Extreme Value Theorem (EVT) is an existence theorem that states if a function is continuous on a closed interval, then it must have both an absolute maximum and an absolute minimum on that interval. It's important because it guarantees the existence of these extrema, which is crucial for analysis.
How does the script define the conditions necessary to guarantee a maximum or minimum value for a graph?
-The script states that the only condition necessary to guarantee a maximum or minimum value for a graph is that the graph must be continuous. Continuity ensures that the extreme value theorem can be applied.
What is the 'candidates test' mentioned in the script and how is it used?
-The 'candidates test' is a method used to find the absolute maximum and minimum values of a function. It involves creating a table with the function's values at critical points and endpoints, then identifying the highest and lowest values from this table.
In the script, how is the derivative of a function used to find critical points?
-The derivative of a function is set equal to zero to find critical points where the function might have a relative extrema. If the derivative is undefined at a point, that point is also considered a critical point.
What is the role of the endpoints in the process of finding the absolute maximum and minimum of a function?
-Endpoints are important because they are included in the 'candidates test' to ensure that the maximum and minimum values of the function on a closed interval are correctly identified, as these values can occur at the endpoints.
Can you provide an example from the script where the derivative of a function is undefined, making it a critical point?
-Yes, in the script, the derivative of the function f(x) = 2x^(-1/3) - 2 is undefined when x = 0, making it a critical point because the derivative does not exist at this value.
How does the script illustrate the process of finding the absolute maximum and minimum for a trigonometric function?
-The script uses the derivative of sin(x^2) and applies the chain rule to find critical points. It then uses the candidates test by plugging in values at critical points and endpoints to find the absolute maximum and minimum values of the function.
Outlines
📚 Understanding Derivatives and Extrema
This paragraph introduces the concept of derivatives and their role in identifying extrema (maximum and minimum points) on a graph. It explains the difference between absolute extrema (global maximum or minimum) and relative extrema (local maximum or minimum). The speaker uses a graph to illustrate these points, noting that absolute extrema occur at the highest and lowest points on the graph within a given interval, while relative extrema occur where the graph changes direction. The concept of critical numbers is introduced, which are points where the derivative is either zero or undefined. A critical theorem is mentioned, stating that relative extrema can only occur at critical numbers. The Extreme Value Theorem (EVT) is briefly touched upon, which guarantees the existence of absolute extrema for continuous functions on a closed interval. The paragraph concludes with a method to find absolute extrema by identifying critical numbers and evaluating the function at these points and the endpoints of the interval.
🔍 Finding Absolute Extrema with Derivatives
The speaker continues the discussion on finding absolute extrema by using derivatives. They demonstrate the process of setting the derivative equal to zero to find critical points, which are potential locations for relative extrema. The importance of checking the end points of the interval is emphasized, as extrema can also occur there. The speaker provides an example with a function and its derivative, showing how to factor the derivative to find critical points. They then use a 'candidates test' to evaluate the function at these critical points and the end points, comparing the values to determine the absolute maximum and minimum. The process is repeated for two more examples, each involving different functions and their derivatives. The speaker highlights the need to consider both critical points and end points to accurately determine the extrema.
📉 Analyzing Trigonometric Functions for Extrema
In this paragraph, the speaker focuses on finding extrema in trigonometric functions using derivatives. They start by taking the derivative of a function involving sine squared and apply the chain rule. The derivative is set to zero to find critical points, considering both where the derivative is zero and where it is undefined. The speaker identifies critical points by solving the equation derived from setting the derivative equal to zero. A 'candidates test' is used again, plugging in the critical points and end points into the original function to find the y-values. The speaker concludes by stating the absolute maximum and minimum values of the function, noting that the maximum occurs at two different points and the minimum at one point. This example illustrates the process of analyzing trigonometric functions to determine their extrema.
Mindmap
Keywords
💡Derivative
💡Extrema
💡Critical Number
💡Absolute Maximum and Minimum
💡Relative Maximum and Minimum
💡Continuous Function
💡Extreme Value Theorem (EVT)
💡Candidates Test
💡Undefined Derivative
💡Chain Rule
💡Sine and Cosine Functions
Highlights
Introduction to derivatives and their significance in understanding the behavior of functions.
Explanation of absolute and relative extrema in the context of graph analysis.
Identification of critical numbers as points where the derivative is zero or undefined.
The theorem that relative extrema can only occur at critical numbers.
Demonstration of finding absolute maximum and minimum values on a graph.
The importance of continuity for the existence of extrema on a graph.
Introduction to the Extreme Value Theorem (EVT) and its implications for continuous functions.
Process of finding critical numbers by setting the derivative equal to zero.
The Candidates Test for determining the absolute maximum and minimum values of a function.
Illustration of the Candidates Test with a specific function and its critical points.
Differentiation between the existence of a maximum and minimum on a graph based on its continuity.
The role of end points in determining the absolute extrema of a function.
Application of the chain rule in finding the derivative of a composite function.
Setting up and solving for critical points in a trigonometric function example.
Using the Candidates Test to find the absolute maximum and minimum for a trigonometric function.
Conclusion of the lesson with a summary of the process for finding absolute extrema.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: