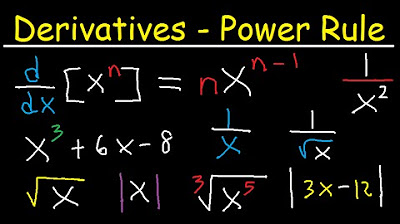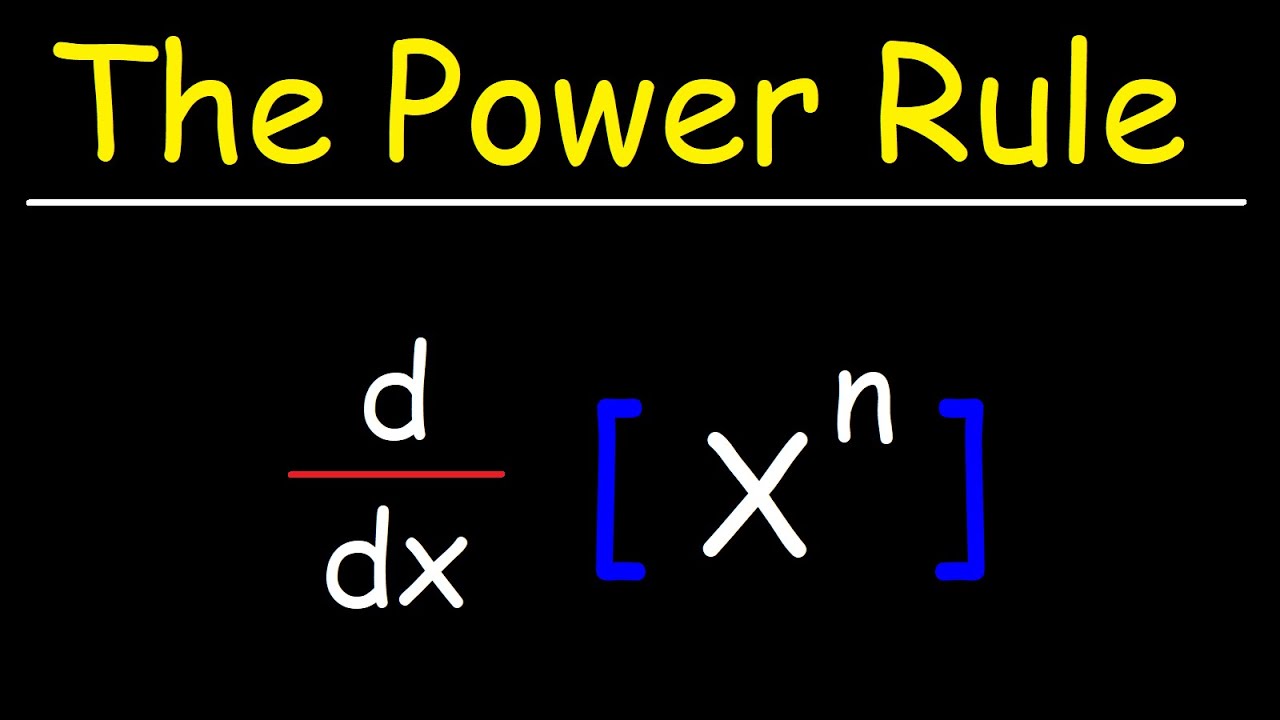Derivatives of Polynomial Functions | Calculus

The Organic Chemistry Tutor
23 Feb 201806:22
EducationalLearning
32 Likes 10 Comments

TLDRThis video lesson covers the concept of derivatives of polynomial functions, walking through the process of finding derivatives using the power rule and constant multiple rule. It demonstrates the steps with various examples, including simplifying expressions before differentiation and handling polynomials divided by monomials. The lesson is a comprehensive guide for understanding how to calculate the first derivative of polynomial functions.

Takeaways
  • 📚 The main topic of the lesson is the derivatives of polynomial functions.
  • 📈 To find the derivative of a polynomial, differentiate each term separately using the power rule and constant multiple rule.
  • 🔢 The derivative of x cubed is 3x squared (using the power rule).
  • 📝 For a constant term, the derivative is 0, as constants do not change with respect to the variable.
  • 🌟 When differentiating a term with a coefficient, multiply the coefficient by the derivative of the variable part.
  • 🛠️ The power rule states that the derivative of x to the power n is n times x to the power (n-1).
  • 🔄 When dealing with a polynomial function that includes multiplication, distribute if necessary to simplify the expression before differentiation.
  • 📊 For a polynomial function that includes a squared term, the derivative is twice the original term (2x for x squared).
  • 📈 When a polynomial is divided by a monomial, simplify by dividing each term's exponent by the denominator's exponent.
  • 📌 The lesson provides examples to illustrate the process of finding derivatives, reinforcing understanding through practice.
Q & A

  • What is the main topic of the lesson?

    -The main topic of the lesson is the derivatives of polynomial functions.

  • How is the derivative of a term like x cubed calculated?

    -The derivative of x cubed is calculated using the power rule, which states that the derivative of x to the n power is n times x to the (n-1) power. So, the derivative of x cubed is 3x squared.

  • What is the constant multiple rule and how is it applied?

    -The constant multiple rule states that the derivative of a constant multiplied by a function is the constant multiplied by the derivative of the function. For example, the derivative of 5x squared is 5 times the derivative of x squared, which is 2x to the first power, resulting in 10x.

  • What is the derivative of a constant in a polynomial function?

    -The derivative of a constant in a polynomial function is always 0, as constants do not change with respect to the variable.

  • How do you find the derivative of a function with terms multiplied together, like 7x times 2x minus x cubed?

    -You distribute the multiplication to each term. For 7x times 2x, you multiply 7x by 2x to get 14x squared. For 7x times negative x cubed, you multiply 7x by -x to the fourth power, resulting in -7x to the fourth power. Then, you find the derivative of each term separately and combine them.

  • What is the chain rule, and how is it used in finding the derivative of an expression like (3x plus two) squared?

    -The chain rule is used when you need to differentiate a composite function. In the case of (3x plus two) squared, you first expand the expression using the distributive property (also known as FOIL), then differentiate each term, and finally combine the derivatives.

  • How do you simplify a function like 4x to the fifth power minus 5x to the fourth power plus 2x to the third, all divided by x squared?

    -You simplify by dividing each term of the polynomial in the numerator by the monomial in the denominator. You subtract the exponents: five minus two is three for the first term, four minus two is two for the second term, and three minus two is one for the third term, resulting in 4x to the third power, 5x squared, and 2x.

  • What is the derivative of the simplified function 4x to the third power minus 5x squared plus 2x?

    -The derivative of 4x to the third power is 12x squared, the derivative of 5x squared is -10x, and the derivative of 2x is 1. So, the derivative of the simplified function is 12x squared minus 10x plus 2.

  • What is the process for finding the derivative of a polynomial function?

    -The process involves taking the derivative of each term separately using the power rule, constant multiple rule, and other relevant differentiation rules. Then, you combine these derivatives to find the overall derivative of the function.

  • Why is it important to simplify a polynomial function before finding its derivative?

    -Simplifying a polynomial function before finding its derivative makes the process easier and less prone to errors. It allows you to clearly see the individual terms and their respective powers, which is crucial for applying the correct differentiation rules.

  • What is the final derivative found in the lesson?

    -The final derivative found in the lesson is 12x squared minus 10x plus 2, derived from the simplified function 4x to the third power minus 5x squared plus 2x.

Outlines
00:00
📚 Introduction to Derivatives of Polynomial Functions

This paragraph introduces the concept of derivatives of polynomial functions, using a specific function as an example. The function given is f(x) = x^3 - 5x^2 + 7x - 4, and the process of finding its derivative is explained step by step. The power rule is applied to each term, resulting in the derivative f'(x) = 3x^2 - 10x + 7. A similar example is provided, where the function is f(x) = 4x^5 - 6x^3 + 8x^2 - 9, and the first derivative is found to be 20x^4 - 18x^2 + 16x. The explanation continues with a third example, emphasizing the importance of distributing and simplifying expressions before finding derivatives, leading to the final derivative f'(x) = 28x - 28x^3.

05:08
📈 Simplifying Complex Polynomial Functions

This paragraph focuses on simplifying complex polynomial functions before finding their derivatives. The example given is f(x) = (3x + 2)^2, which is expanded using the FOIL method to 9x^2 + 12x + 4. The derivative is then found by applying the power rule to each term, resulting in f'(x) = 18x + 12. Another example is provided where a polynomial is divided by a monomial, and the process involves dividing each term of the polynomial by the monomial. The derivative is then found by applying the power rule, leading to the result f'(x) = 12x^2 - 10x + 2.

Mindmap
Keywords
💡Derivatives
Derivatives are a fundamental concept in calculus that represent the rate of change or the slope of a function at any given point. In the context of this video, the focus is on computing the derivatives of polynomial functions, which involves applying rules such as the power rule and the constant multiple rule. For instance, the derivative of x cubed is calculated as 3x squared, illustrating how the power rule is used to find the rate of change for each term in the polynomial function.
💡Polynomial Functions
Polynomial functions are mathematical expressions consisting of variables and coefficients, involving only the operations of addition, subtraction, multiplication, and non-negative integer exponents of variables. In the video, several examples of polynomial functions are given, such as f(x) = x^3 - 5x^2 + 7x - 4, and the process of finding their derivatives is explained step by step. Polynomial functions are essential in various mathematical and real-world applications due to their simplicity and the ease with which their derivatives can be calculated.
💡Power Rule
The power rule is a fundamental rule in calculus that is used to find the derivative of a term with a variable raised to a power. According to the power rule, the derivative of x^n (where n is a constant) is n*x^(n-1). This rule is applied multiple times throughout the video to calculate the derivatives of terms like x^5 or x^3. For example, the derivative of x^3 is 3x^2, demonstrating how the power rule helps in determining the rate of change for each term in a polynomial function.
💡Constant Multiple Rule
The constant multiple rule states that the derivative of a constant multiplied by a function is the constant multiplied by the derivative of the function. In the video, this rule is used when differentiating terms like -5x^2 or 7x. For instance, the derivative of -5x^2 is -5 * 2x, which equals -10x, showing how the constant multiple rule simplifies the process of finding the derivative of a polynomial function by separating the constant from the variable part.
💡Chain Rule
The chain rule is a crucial concept in calculus used when dealing with composite functions, which are functions composed of other functions. Although not explicitly mentioned in the video, the chain rule would be relevant if the function involved terms like (g(x)) where g(x) is another function. The chain rule states that the derivative of a composite function is the derivative of the outer function times the derivative of the inner function. For example, if f(x) = (3x + 2)^2, you would use the chain rule to find the derivative of the outer function (square) with respect to the inner function (3x + 2).
💡Simplifying
Simplifying is the process of making a mathematical expression easier to understand or calculate by reducing it to a simpler form. In the video, simplifying is crucial before finding the derivative of more complex functions, such as a polynomial divided by a monomial. For example, the function 4x^5 - 5x^4 + 2x^3 divided by x^2 is simplified by subtracting the exponents, resulting in 4x^3 - 5x^2 + 2x, which is then differentiated to find the result 12x^2 - 10x + 2.
💡Rate of Change
The rate of change is a fundamental concept in calculus that describes how a quantity changes in response to a change in another quantity. In the context of this video, the derivatives of polynomial functions represent their rates of change. For instance, the derivative 3x^2 - 10x + 7 represents the rate at which the function f(x) = x^3 - 5x^2 + 7x - 4 changes at any given value of x. Understanding the rate of change is essential for analyzing the behavior of functions and their applications in various fields.
💡Differentiation
Differentiation is the process of finding the derivative of a function, which gives us information about the function's behavior, such as its rate of change or slope at any point. In this video, differentiation is the primary operation performed on polynomial functions to find their derivatives. For example, differentiating the function f(x) = 4x^5 - 6x^3 + 8x^2 - 9 results in 20x^4 - 18x^2 + 16x, which is the first derivative of the original function.
💡Foil Method
The FOIL method is a technique used to expand the product of two binomials (two terms with variables). It stands for First, Outer, Inner, and Last, which refers to the four terms obtained when two binomials are multiplied. In the video, the FOIL method is used to expand expressions like (3x + 2)^2, resulting in 9x^2 + 12x + 12x + 4. This method is crucial for simplifying expressions before differentiating them, as it allows for the application of other rules such as the power rule and the constant multiple rule.
💡Slope
Slope refers to the measure of the steepness of a straight line, or in the context of a function, the rate at which the function values change. In the video, the derivative of a function represents its slope at any given point. For example, the derivative 3x^2 - 10x + 7 for the function f(x) = x^3 - 5x^2 + 7x - 4 indicates the slope of the function at different points on its graph. Understanding the slope is essential for analyzing the function's behavior, such as whether it is increasing or decreasing at a particular point.
💡Exponents
Exponents are mathematical symbols that indicate the number of times a base is multiplied by itself. In the video, exponents are used in polynomial functions to denote the power to which a variable is raised. For instance, in the function f(x) = x^5 - 6x^3 + 8x^2 - 9, the exponents 5, 3, 2, and 0 indicate the respective powers of x. When finding derivatives, the power rule is applied, which involves adjusting the exponents to calculate the rate of change for each term in the polynomial.
Highlights

Derivatives of polynomial functions are discussed in the lesson.

The derivative of a function is the slope of the tangent line at any point on the curve of the function.

For the function f(x) = x^3 - 5x^2 + 7x - 4, the derivative is found by applying the power rule to each term.

The power rule states that the derivative of x^n is n*x^(n-1).

The derivative of x^3 is 3x^2.

The constant multiple rule is used when a term has a coefficient, which is a constant.

The derivative of 5x^2 is 10x, by applying the constant multiple rule.

The derivative of a constant is 0.

For the function f(x) = 4x^5 - 6x^3 + 8x^2 - 9, the first derivative is calculated by applying the power rule to each term.

The derivative of x^5 is 5x^4.

The derivative of x^3 is 3x^2.

The derivative of x^2 is 2x.

For a function like 7x(2x - x^3), distribute the coefficient 7x to each term inside the parentheses.

The derivative of a product of two functions requires the use of the product rule, which was not explicitly mentioned but is implied in the process.

For the function f(x) = (3x + 2)^2, the first derivative is found by expanding the expression and applying the power rule to each term.

The chain rule is used when differentiating a composite function, which was not directly discussed but is relevant to the process of expanding and differentiating.

The derivative of 9x^2 is 18x.

The derivative of a polynomial function involves applying the power rule to each term and combining the results.

For a function like 4x^5 - 5x^4 + 2x^3 divided by x^2, simplify the expression before finding the derivative.

When dividing a polynomial by a monomial, subtract the exponents of like bases.

The derivative of the simplified function 4x^3 - 5x^2 + 2x is 12x^2 - 10x + 2.

Transcripts

Browse More Related Video

Calculus 1 - Derivatives

Derivatives - Power Rule

The Power Rule For Derivatives

The Constant Multiple Rule For Derivatives

AP Calculus AB: Lesson 3.1 Elementary Derivative Rules

Finding 2nd Derivatives

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativesPolynomial FunctionsMathematics TutorialPower RuleConstant Multiple RuleChain RuleEducational ContentMathematics EducationAlgebraic ConceptsCalculus Fundamentals