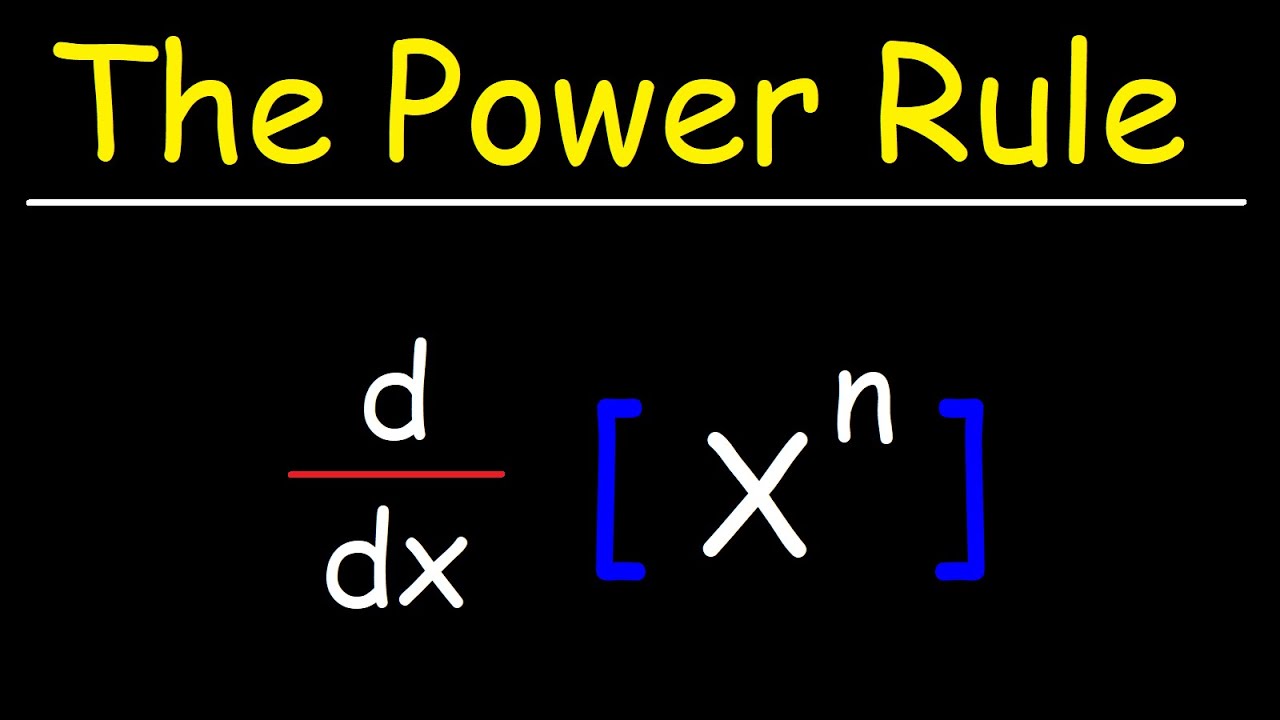The Constant Multiple Rule For Derivatives

The Organic Chemistry Tutor
23 Feb 201814:46
EducationalLearning
32 Likes 10 Comments

TLDRThis video script offers a comprehensive guide to the constant multiple rule in calculus, focusing on how to differentiate functions involving constants and variables. By using the power rule and providing clear examples, the lesson demonstrates how to find derivatives of expressions like 3x^5, 4x^7, and more complex rational functions and roots. The explanation simplifies the process into manageable steps, making calculus more accessible and understandable.

Takeaways
  • 📚 The Constant Multiple Rule states that the derivative of a constant times a function is equal to the constant times the derivative of the function.
  • 🔢 To differentiate a constant multiplied by a variable to a power, use the Power Rule: (n * x^(n-1))
  • 🌟 Example: The derivative of 3x^5 is 15x^4, applying both the constant multiple and power rules.
  • 📈 For a fraction with a variable divided by a constant, rewrite the expression as the constant times the variable to apply the constant multiple rule.
  • 🌐 When differentiating a function with a constant coefficient, separate the variable from the constant to identify the derivative of the variable part.
  • 🛠️ The derivative of x^3 / 15 can be simplified by canceling common factors and rewriting the result as x^2/5 or 15x^2.
  • 🎓 For square root functions, rewrite the square root as the exponent (1/2) and apply the power rule, resulting in the derivative of 4√x as 2/√x.
  • 📊 When dealing with rational functions, invert the fraction to make the variable the numerator and apply the power rule to the variable part.
  • 🌠 To find the derivative of an expression with a root, first convert the root to an exponent, then apply the power rule, and convert back to radical form if necessary.
  • 🔄 Example: The derivative of (5/2)^(1/7)√x^4 is simplified to -10/7 * √(x^4) after applying the rules and simplifying.
  • 🔧 Rationalize the denominator if necessary by multiplying the numerator and denominator by the conjugate of the denominator to eliminate radicals.
Q & A

  • What is the constant multiple rule for derivatives?

    -The constant multiple rule for derivatives states that the derivative of a constant times a function is equal to the constant times the derivative of the function.

  • How do you differentiate a constant multiplied by a variable raised to a power?

    -To differentiate a constant multiplied by a variable raised to a power, you first find the derivative of the variable using the power rule, and then multiply it by the constant.

  • What is the power rule for differentiation?

    -The power rule for differentiation states that the derivative of a variable x raised to a constant n is n times x raised to the power n minus one.

  • How do you find the derivative of a fraction where the numerator is a variable and the denominator is a constant?

    -To find the derivative of such a fraction, you rewrite the expression as the constant (which is the denominator) divided by the variable (which is the numerator), and then apply the constant multiple rule.

  • What is the process for differentiating a function that involves a square root?

    -To differentiate a function involving a square root, you first rewrite the square root as the variable raised to the power of one half, and then apply the power rule to find the derivative.

  • How do you simplify the derivative of a function with a negative exponent?

    -To simplify the derivative of a function with a negative exponent, you convert the negative exponent to a positive one by flipping the variable and the exponent, and then simplify the expression if possible.

  • What is the derivative of x divided by seven?

    -The derivative of x divided by seven is 1 divided by 7, since the derivative of x to the first power is 1 and anything to the zero power is 1.

  • How do you differentiate x cubed divided by 15?

    -To differentiate x cubed divided by 15, you apply the constant multiple rule. The derivative is (1 over 15) times the derivative of x cubed, which is 3x squared. After simplifying, the answer is x squared over 5.

  • What is the derivative of negative seven x to the sixth divided by four?

    -The derivative of negative seven x to the sixth divided by four is negative 42 x to the fifth divided by two, which simplifies to negative 21 x to the fifth divided by two.

  • What is the derivative of 4 square root x?

    -The derivative of 4 square root x is 2 divided by x to the one half, which can also be expressed as two times the square root of x.

  • How do you differentiate 5 divided by x to the negative 1?

    -To differentiate 5 divided by x to the negative 1, you apply the power rule. The derivative is negative 5 divided by x squared.

  • What is the derivative of five divided by two times the seventh root of x to the fourth?

    -The derivative of five divided by two times the seventh root of x to the fourth is negative 10 divided by 7 times the seventh root of x to the eleventh power, which can be further simplified to negative 10 divided by 7 times x times the 7th root of x to the fourth power.

Outlines
00:00
📚 Constant Multiple Rule for Derivatives

This paragraph introduces the constant multiple rule for derivatives, a fundamental concept in calculus. It explains that the derivative of a constant times a function is equal to the constant times the derivative of the function. The explanation is illustrated with examples, such as differentiating 3x^5 using the power rule, resulting in 15x^4. The paragraph also covers how to handle fractions by separating the constant from the variable, as demonstrated in finding the derivative of x/7. The process is further applied to more complex examples, including rational functions and square root functions, emphasizing the use of the power rule and the importance of simplifying the final results.

05:03
🔢 Working with Rational Functions and Square Roots

The second paragraph delves into applying the constant multiple rule to more complex mathematical expressions involving rational functions and square roots. It demonstrates how to differentiate expressions like 4√x by rewriting the square root as x^(1/2) and then applying the power rule, resulting in 2/√x. The paragraph also addresses the differentiation of rational functions, such as 5/x, by inverting the function and using the power rule to find the derivative, which is -5/x^2. Additionally, it explains how to simplify derivatives involving radicals by converting them into exponential form, as shown in the example of 5/(2^(7/4)x^(4/7)), and further simplifying the result by separating the radicals and rationalizing the expression if necessary.

10:05
🌟 Advanced Derivative Simplification

The third paragraph focuses on the advanced simplification of derivatives, particularly those involving complex radical expressions. It guides through the process of differentiating and simplifying expressions like 5/(2^(7/4)x^(4/7)), resulting in -10/(7x^(11/7)). The explanation includes moving variables to the top, changing negative exponents to positive ones, and simplifying radical expressions by separating them into simpler radicals and rationalizing if required. The paragraph emphasizes the importance of breaking down complex expressions into manageable parts and using mathematical rules to arrive at a simplified, understandable form.

Mindmap
Keywords
💡Derivative
In the context of the video, a derivative refers to the mathematical concept that represents the rate of change or the slope of a function at a specific point. It is a fundamental concept in calculus and is used to analyze the behavior of functions. The video discusses the process of finding derivatives using the constant multiple rule, which is applied to various examples throughout the lesson.
💡Constant Multiple Rule
The constant multiple rule is a principle in calculus that states the derivative of a constant multiplied by a function is equal to the constant multiplied by the derivative of the function alone. This rule simplifies the process of differentiation by allowing students to separate the constant from the variable and deal with them independently. The video provides several examples to illustrate how to apply this rule to functions involving constants and variables raised to various powers.
💡Power Rule
The power rule is a fundamental differentiation rule that allows the calculation of the derivative of a variable raised to a constant power. According to the rule, the derivative of x^n (where n is a constant) is n*x^(n-1). The video script uses the power rule to find the derivatives of functions like x to the fifth power and x to the ninth power, demonstrating how this rule interacts with the constant multiple rule.
💡Variable
In mathematics and the context of this video, a variable is a symbol, often a letter like 'x', that represents an unknown quantity or a value that can change. Variables are essential in functions and equations, and the video discusses differentiating functions with respect to variables, such as finding the derivative of x to various powers.
💡Function
A function is a mathematical relationship between two or more variables, typically expressed as y = f(x), where 'y' is the dependent variable and 'x' is the independent variable. The video focuses on the differentiation of functions, which is the process of finding the derivative, a measure of how the function changes as the input variable changes.
💡Differentiate
In the context of the video, to differentiate a function means to find its derivative, which is the mathematical representation of the function's rate of change. Differentiation is a core operation in calculus and is used to analyze various properties of functions, such as their slopes, critical points, and maximum or minimum values.
💡Slope
The slope of a function at a particular point is a measure of how steep the graph of the function is at that point. It is a concept closely related to derivatives, as the derivative of a function at a point is the slope of the tangent line to the graph of the function at that point. The video discusses the concept of slope while explaining the process of differentiation.
💡Rational Functions
Rational functions are mathematical expressions that involve a ratio of two polynomial functions. In the video, the concept of rational functions is introduced when discussing the differentiation of expressions like 5 divided by x. Rational functions are significant in calculus because they can represent a wide variety of behaviors, including asymptotes and holes in their graphs.
💡Radical Form
Radical form refers to the representation of a mathematical expression in terms of roots, such as the square root of x (x^(1/2)) or the cube root of x (x^(1/3)). The video script discusses converting expressions from radical form to exponential form and back again, as part of the process of differentiating complex functions involving roots.
💡Exponential Form
Exponential form is a way of expressing mathematical relationships where one quantity is an exponent, such as x^(4/7) representing x to the fourth power divided by seven. The video explains how to convert expressions from radical form to exponential form, which is useful for differentiating functions that involve roots and for simplifying the resulting derivatives.
💡Rationalize
Rationalizing is the process of eliminating radicals or roots from the denominator of a fraction. In the video, this concept is briefly mentioned in the context of simplifying the final answer of a differentiation problem involving radicals in the denominator. Rationalization often involves multiplying the numerator and denominator by a specific expression to create a rational denominator.
Highlights

The introduction of the constant multiple rule for derivatives, a fundamental concept in calculus.

The derivative of a constant times a function is the constant times the derivative of the function.

Example given: Differentiating 3x to the fifth power using the constant multiple rule and power rule.

Derivative calculation: 3x^5 becomes 15x^4 after applying the rules.

Instructions to find the derivative of 4x to the seventh power and 5x to the ninth power.

Derivative of a fraction involving a variable divided by a constant; rewriting and applying the constant multiple rule.

Derivative of x divided by seven calculated to be 1/7.

Example of differentiating a more complex fraction: x cubed divided by 15.

Derivative of negative seven x to the sixth divided by four; separating variable and constant, and simplifying the result.

Application of the constant multiple rule to square root functions, specifically the derivative of 4 square root x.

Derivative of 4 square root x calculated to be 2/x^(1/2).

Differentiating rational functions, such as 5 divided by x, using the constant multiple rule.

Derivative of 5/x calculated to be -5/x^2.

Working with more complex rational functions, like 5 divided by two and the seventh root of x to the fourth.

Derivative of the complex rational function calculated to be -10/7 times the seventh root of x to the eleventh.

Further simplification of the derivative of the complex rational function by separating radicals and rationalizing the expression.

Final simplified form of the derivative expressed both in radical and rational forms for clarity.

Transcripts

Browse More Related Video

Derivatives of Rational Functions

The Chain Rule - Part 2

Calculus 1 - Derivatives

How To Find The Derivative of a Fraction - Calculus

The Power Rule For Derivatives

Derivatives of Polynomial Functions | Calculus

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
DerivativesCalculusMath EducationPower RuleConstant MultipleRational FunctionsSquare RootsOnline LearningMath TutorialAdvanced Math