Derivatives - Power Rule
TLDRThis video script offers a comprehensive guide on derivatives, focusing on the power rule for functions and its application to various types of functions, including polynomials, square roots, rational functions, and absolute values. The video begins by explaining the power rule, which states that the derivative of x raised to a power is the power times x to the power minus one. Several examples illustrate this rule, such as finding the derivatives of x cubed, x to the fourth, fifth, sixth, and seventh powers, and handling constants. The script also covers the differentiation of functions with multiple terms and the process for finding higher-order derivatives. Additionally, it explores derivatives of functions like 1/x, square roots, and cube roots, emphasizing the need to rewrite functions before applying the power rule. The video concludes with a discussion on the derivative of absolute value functions, noting the discontinuity at certain points and how to express the derivative as a piecewise function. The script is an excellent resource for those looking to understand the basics of differentiation and its application to different mathematical scenarios.
Takeaways
- 📚 The power rule states that the derivative of x raised to a power is that power times x to the power minus one.
- 🔢 For example, the derivative of x^3 is 3x^2, and the derivative of x^4 is 4x^3.
- 📈 The derivative of a constant multiple of a function, like 4x^3, is the constant multiple times the derivative of the function itself.
- 🎓 Constants like e and π, when multiplied by x, result in the derivative being just the constant, as their derivative is zero.
- ∑ When finding the derivative of a function with multiple terms, differentiate each term separately and sum the results.
- 🔄 To find the derivative of a function like 1/x, rewrite it as x to the -1 and apply the power rule.
- √ The square root of x is equivalent to x^(1/2), and its derivative is (1/2)x^(-1/2).
- ∛ For roots other than square roots, like the cube root of x^5, rewrite as x^(5/3) and apply the power rule.
- ⏸ At points of non-differentiability, such as the vertex of an absolute value function, the derivative does not exist.
- 📉 The absolute value function can be broken into two parts: positive x when x ≥ 0 and negative x when x < 0, each with its own derivative.
- 🤔 To find the derivative of a complex function, like the absolute value of 3x - 12, first express it as a piecewise function and then find the derivative for each piece.
Q & A
What is the power rule for finding the derivative of a function?
-The power rule states that the derivative of x raised to some power n is equal to n times x raised to the power n minus one (d/dx(x^n) = n*x^(n-1)).
How do you find the derivative of x cubed?
-Using the power rule, the derivative of x cubed (x^3) is 3 times x squared (3x^2).
What is the derivative of a constant multiple of a function?
-The derivative of a constant multiple of a function is the constant multiplied by the derivative of the function. For example, the derivative of 4x^3 is 12x^2.
Why is the derivative of a constant equal to zero?
-The derivative of a constant is zero because constants do not change with respect to the variable x, so their rate of change is zero.
How do you find the derivative of a polynomial function?
-To find the derivative of a polynomial function, you differentiate each term separately using the power rule and then sum the results.
What is the process to find the derivative of 1 over x?
-First, rewrite 1 over x as x to the power of negative one. Then, apply the power rule by moving the exponent to the front and subtracting one from the exponent to get the derivative -1/x^2.
How can you find the derivative of the square root of x?
-The square root of x is equivalent to x to the power of 1/2. Using the power rule, the derivative is 1/2 times x to the power of -1/2.
What is the derivative of the cube root of x to the fifth power?
-First, rewrite the cube root of x to the fifth power as x to the power of 5/3. Then, apply the power rule to get the derivative as 5/3 times x to the power of 2/3.
What is the derivative of a function with absolute value?
-The derivative of a function with an absolute value is a piecewise function. It is the derivative of the inside function for the respective intervals where the inside function is positive or negative.
Why is the absolute value function not differentiable at the vertex of its graph?
-The absolute value function is not differentiable at the vertex because the slope changes instantaneously, resulting in a discontinuity in the derivative at that point.
How do you find the derivative of a rational function?
-To find the derivative of a rational function, you can separate the fraction into two fractions if the denominator has only one term, then differentiate each term separately and simplify the result.
Outlines
📚 Introduction to Derivatives and Power Rule
The video begins by introducing the concept of derivatives and the power rule for finding them. It explains that the derivative of x raised to a power is that power times x to the power minus one. Several examples are provided, including derivatives of x cubed, x to the fourth, fifth, sixth, and seventh powers, as well as constants and polynomials. The constant multiple rule is also discussed, and the video touches on the derivatives of constants like e and pi, which are zero.
🔢 Derivatives of Polynomials, Roots, and Rational Functions
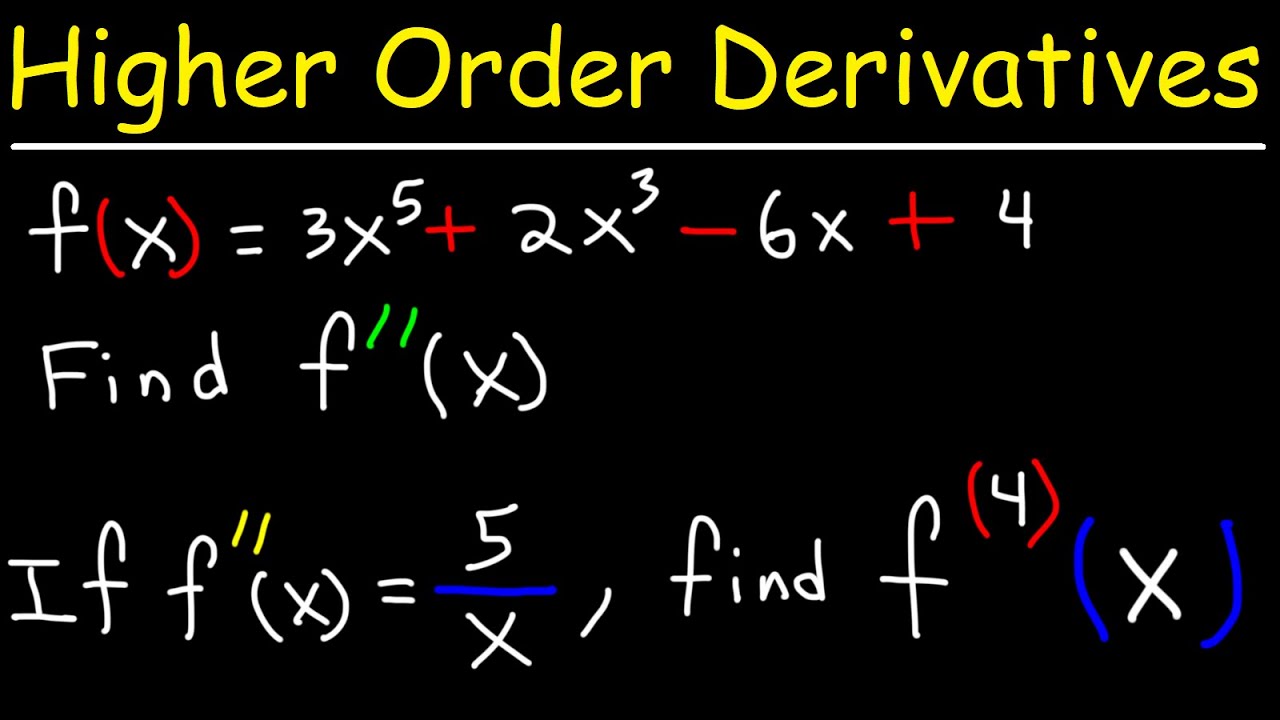
This paragraph delves into finding derivatives of more complex functions, including polynomials, square roots, and rational functions. It covers the process of differentiating each term of a function separately and combining the results. Examples given include finding the first and second derivatives of functions involving x cubed, x squared, and constants. The video also provides a method to find derivatives of functions like 1/x by rewriting the function and applying the power rule.
🔄 Derivatives of Functions with Roots and Radicals
The third paragraph focuses on derivatives of functions involving roots and radicals, such as the cube root of x and 1 divided by the square root of x. It demonstrates how to rewrite these functions as powers of x and then apply the power rule to find their derivatives. The process includes simplifying the results and, when necessary, rationalizing the denominator. The video also addresses how to handle derivatives of functions that are not differentiable at certain points, such as at the vertex of an absolute value function.
📉 Derivatives of Absolute Value Functions
This section discusses the derivatives of absolute value functions. It explains that the absolute value function can be represented as a piecewise function and that it is not differentiable at the vertex. The video shows how to find the derivative by considering the function's behavior on either side of the vertex and provides an example of the absolute value of 3x minus 12. It also covers how to represent the derivative as a piecewise function, reflecting the change in slope at the points where the original function is not differentiable.
🔁 Derivatives of Functions with Absolute Values and Final Thoughts
The final paragraph summarizes the process of finding derivatives of functions with absolute values, emphasizing the need to break the function into separate cases based on the value of x. It corrects a previous mistake regarding the sign of the function when x is greater than 4. The video concludes by reminding viewers of the importance of understanding the requirements of their specific course or assignment, as the level of simplification needed may vary. It also encourages viewers to check out additional resources for a comprehensive review of derivatives.
Mindmap
Keywords
💡Derivatives
💡Power Rule
💡Polynomials
💡Square Root Functions
💡Rational Functions
💡Absolute Value
💡Piecewise Function
💡Constant Multiple Rule
💡Chain Rule
💡Trigonometric Functions
💡Exponential Functions
Highlights
The power rule states that the derivative of x raised to a power is that power times x to the power minus one.
Derivative of x cubed is 3x squared, following the power rule by bringing the exponent to the front and subtracting one.
For x to the fourth power, the derivative is four x cubed, showcasing the application of the power rule.
The derivative of a constant multiple of a function, such as 4x cubed, is found by differentiating the function and then multiplying by the constant.
Constants like e and pi, when multiplied by x, have a derivative that is simply the constant, as their power to x is zero.
The derivative of any constant is zero, as nothing raised to the power of zero equals one, and multiplying by zero gives zero.
For a polynomial function, differentiate each term separately and then combine to find the overall derivative.
The derivative of 1 over x is found by rewriting the function as x to the negative one and applying the power rule.
Functions with roots, such as the square root of x, are rewritten as x to the power of one-half before differentiating.
The cube root of x to the fifth power is rewritten as x to the power of five-thirds before finding its derivative.
When differentiating a function with a radical in the denominator, the negative exponent is used to find the derivative.
For rational functions or fractions, separate the numerator and denominator into individual terms before differentiating.
The absolute value function is not differentiable at the point where the sign of x changes, as the slope is discontinuous.
The derivative of the absolute value function is a piecewise function with a slope of one for positive x and negative one for negative x.
When the absolute value function includes a linear term, such as |3x - 12|, the vertex and the slopes on either side of the vertex are used to find the derivative.
The derivative of a function involving an absolute value must be expressed as a piecewise function to account for the change in slope.
Differentiating a function requires understanding the function's behavior and applying the appropriate rules for different types of functions.
The video offers a comprehensive review of derivatives, including power, product, quotient, and chain rules, as well as derivatives of trigonometric and exponential functions.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: