Finding 2nd Derivatives
TLDRThis video script provides a comprehensive guide on finding second derivatives of functions. It begins by explaining that the second derivative is the derivative of the first derivative, and continues with several examples to illustrate the process. The first example involves a polynomial function, where the first and second derivatives are calculated step by step. The video also touches on higher-order derivatives, noting that while they are less common, they can be found by continuing to differentiate. Subsequent examples explore different types of functions, including linear, exponential, and logarithmic, each requiring specific rules such as the product rule or chain rule for differentiation. The script emphasizes the importance of understanding the underlying principles of differentiation, as well as the practical applications of second derivatives in various mathematical and real-world scenarios. The summary serves to engage users with a clear and concise overview of the video's content, inviting them to delve deeper into the topic.
Takeaways
- 📚 The second derivative is found by taking the derivative of the first derivative, denoted with two prime marks.
- 🔢 The first derivative of a function is calculated by differentiating the original function.
- 🔧 The process of finding the second derivative involves applying differentiation rules such as the power rule and the product rule.
- 🔁 Derivatives can be taken multiple times, although the second derivative is most commonly used in calculus.
- 🔃 For the function e^(-x), the second derivative is the same as the original function, and its derivatives alternate between positive and negative.
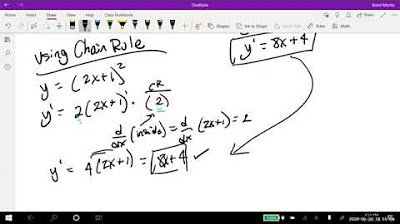
- ⛓ When using the chain rule, the derivative of a composite function is the derivative of the outer function times the derivative of the inner function.
- 🔄 The product rule states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.
- 📉 For functions involving logarithms or negative exponents, rewrite them in a form that allows for easier application of derivative rules.
- 🧹 After finding the second derivative, it's often helpful to simplify and rewrite the expression in a more standard mathematical form.
- 🚫 It's not common to take a third derivative in most calculus problems, but it's possible and would follow the same process as finding the second derivative.
- ∞ Some functions, like e^x or e^(-x), can have an infinite number of derivatives, which can be found by continuously differentiating.
Q & A
What is the first step in finding the second derivative of a function?
-The first step is to find the first derivative of the function, which is done by differentiating the original function.
How is the first derivative of a function represented in notation?
-The first derivative is represented with a single prime mark (') after the function name, e.g., f'(x).
What does the notation with two prime marks signify in calculus?
-The notation with two prime marks ('') signifies the second derivative of a function.
How is the second derivative of a function found?
-The second derivative is found by taking the derivative of the first derivative.
Is it possible to take more than two derivatives of a function?
-Yes, it is possible to take more derivatives, such as a third, fourth, or even an infinite number of derivatives, depending on the function.
What is the derivative of the function f(x) = e^(-x) with respect to x?
-The derivative of f(x) = e^(-x) is f'(x) = -e^(-x), which is found using the chain rule.
How does the derivative of a function behave when the function is e^(-x)?
-The derivatives of the function e^(-x) alternate between positive and negative and repeat the pattern of the original function indefinitely.
What rule is used to find the derivative of a product of two functions?
-The product rule is used to find the derivative of a product of two functions.
What is the derivative of x * e^x with respect to x?
-The derivative of x * e^x is e^x + x * e^x, which is found by applying the product rule.
How can you rewrite the function x^(-1) + log(x) to apply derivative rules?
-The function can be rewritten as 1/x + log(x), which separates the terms to make it easier to apply derivative rules.
What is the second derivative of the function x^(-1) + log(x)?
-The second derivative is 2/x^3 - 1/x^2, after simplifying and cleaning up the expression obtained from differentiating the first derivative.
What is the final expression for the second derivative of the function -2x^(-2) + x^(-1/2)?
-The second derivative is -12/x^4 + (3/2)x^(-1/2), which is simplified to -12/x^4 + sqrt(x)/x^2.
Outlines
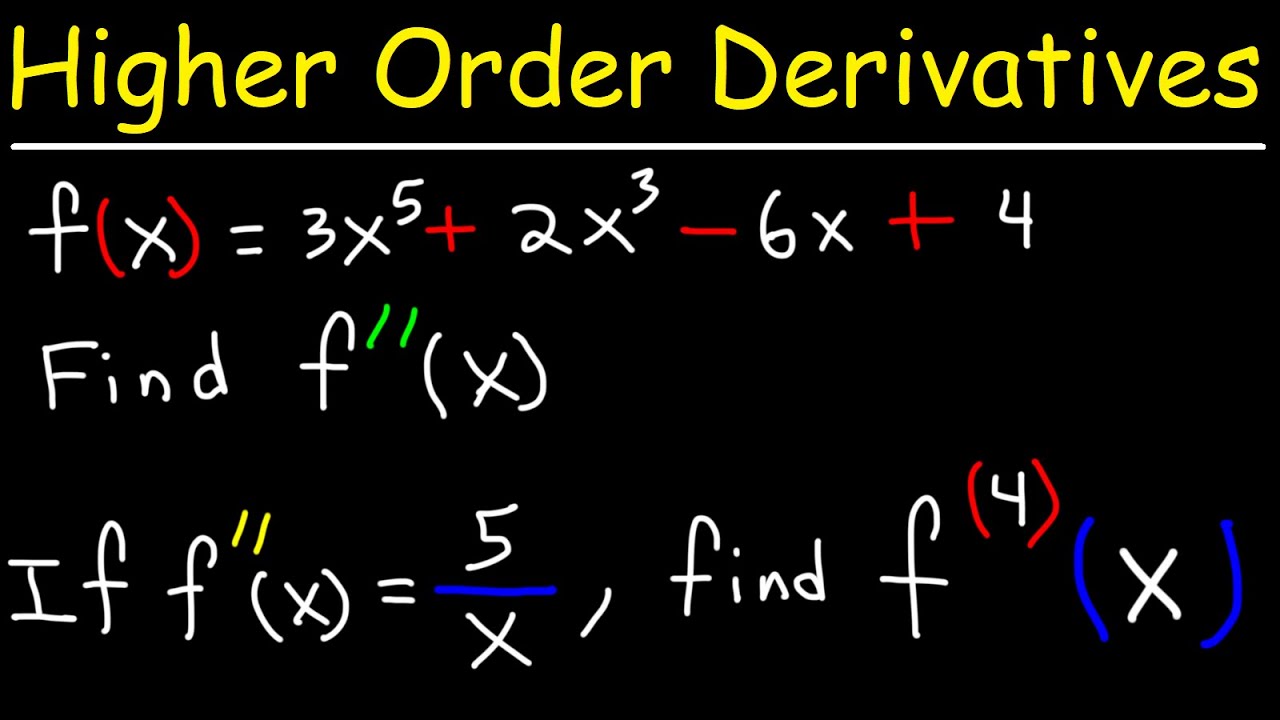
📚 Understanding Higher-Order Derivatives
This paragraph introduces the concept of higher-order derivatives, focusing primarily on the second derivative but also mentioning third and further derivatives. It begins by defining the first derivative as the derivative of a function and the second derivative as the derivative of the first derivative. Examples include polynomial functions and exponential functions. The paragraph emphasizes the application of basic calculus rules like the chain rule and the product rule to find these derivatives, and notes that while higher derivatives are possible, the second derivative is often the most sought after in many practical scenarios.
🔍 Detailed Examples of Calculating Second Derivatives
This paragraph provides specific examples of calculating second derivatives using different calculus rules. It starts with a function involving exponential terms, illustrating how the product rule is used. The second derivative is shown to sometimes simplify to a form similar to the original function, as in the case with the exponential function where the second derivative mirrors the first. Further, it details a situation with a logarithmic and a reciprocal function, demonstrating how derivatives can progressively get more complex to handle. It concludes by illustrating a complex calculation involving fractional powers and how to simplify the expression for practical use.
Mindmap
Keywords
💡Derivative
💡First Derivative
💡Second Derivative
💡Chain Rule
💡Product Rule
💡Function
💡Exponential Function
💡Logarithmic Function
💡Power Function
💡Instantaneous Rate of Change
💡Acceleration
Highlights
The video explains how to find second derivatives of a function.
First derivative is found by taking the derivative of the original function.
Second derivative is found by taking the derivative of the first derivative.
Example 1: First derivative is 15x^4 - 16x^3 + 4x.
Example 1: Second derivative is 60x^3 - 48x^2 + 4.
Higher order derivatives like third and fourth can also be found.
Example 2: First derivative is -6x^2 + 10x.
Example 2: Second derivative is -12x + 10.
Example 3: f(x) = e^(-x), first derivative uses chain rule.
Example 3: Second derivative is the same as the original function.
Derivatives of this function alternate between positive and negative infinitely.
Example 4: Product rule used for derivative since there are two functions.
Example 4: First derivative is e^x + xe^x.
Example 4: Second derivative is 2e^x + xe^x.
Example 5: Function rewritten as x^(-1) + log(x) for easier differentiation.
Example 5: First derivative is -x^(-2) + x^(-1).
Example 5: Second derivative is 2/x^3 - 1/x^2.
Example 6: Original function rewritten for easier differentiation.
Example 6: First derivative is 4x^(-3) - (3/2)x^(-3/2).
Example 6: Second derivative is -12/x^4 + (3/4)√x^5.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: