The Derivative in Calculus Defined as a Limit - [1-2]

Math and Science

1 Dec 202221:51

EducationalLearning

32 Likes 10 Comments

TLDRThe video script provides a clear and detailed explanation of the concept of derivatives in calculus. It introduces the derivative as the slope of a line tangent to a curve at a specific point, using the example of a graph with a function. The script explains the general formula for the slope of a line and how to apply it to find the derivative at a point. It also demonstrates the process of taking the limit as h approaches zero to refine the slope from a line segment to the precise tangent. The video uses examples to illustrate the calculation of derivatives and emphasizes that while the concept is fundamental, the specific formula used is not typically applied in everyday calculus work. The script concludes by highlighting the practical applications of derivatives, such as in determining velocity and acceleration.

Takeaways

📈 The concept of a derivative is introduced as the slope of a line or tangent to a curve at a specific point.
📌 The definition of a derivative is presented as the limit of the difference quotient as the change in the independent variable approaches zero.
🔢 The general formula for the slope of a line is derived from the rise over run, which is applied to understand the concept of a derivative.
🤔 The process of finding the derivative involves calculating the difference in y-values (rise) and x-values (run) between two points on a curve.
🏁 The importance of understanding limits is emphasized as a fundamental aspect of calculus, despite their abstract nature.
📚 The example of the position function P(t) = t^2 - 6t - 5 is used to demonstrate how to evaluate the derivative at a specific point.
🔄 The concept of shrinking the distance between two points on a curve (as H approaches 0) to find the slope of the tangent line is explained.
📈 The derivative of a function can be found using the limit process, which simplifies to a function that predicts the slope at any point on the curve.
🌟 The derivative of a linear function (e.g., f(x) = 5x + 3) is shown to be the constant slope of the line.
🛠️ Practical applications of derivatives, such as relating position functions to velocity and acceleration, are briefly mentioned.
📖 The script encourages learning the limit process for understanding where derivatives come from, but emphasizes that direct methods for finding derivatives are more commonly used in practice.

Q & A

What is the definition of a derivative mentioned in the script?
-The derivative is defined as the slope of the line tangent to a curve at a specific point.
How is the slope of a line calculated?
-The slope of a line is calculated using the formula rise over run, which is the difference in y-values divided by the difference in x-values between any two points on the line.
What is the purpose of finding the derivative of a function?
-The purpose of finding the derivative of a function is to determine the rate of change or the slope of the tangent line to the curve at a specific point, which can be used to analyze various properties of the function.
What does the limit in the definition of the derivative represent?
-The limit in the definition of the derivative represents the process of shrinking the distance between two points on the curve (as H approaches 0) to find the exact slope of the tangent line at a specific point P.
How is the derivative of a function evaluated at a specific point?
-The derivative of a function is evaluated at a specific point by taking the limit as H approaches 0 of the difference in y-values (f(a+h) - f(a)) divided by the difference in x-values (h).
What is the role of limits in calculus?
-Limits in calculus are a fundamental concept used to describe the behavior of a function as the input (or another variable) approaches a certain value. They are essential in defining derivatives and understanding the behavior of functions near specific points.
How does the script illustrate the concept of a derivative?
-The script illustrates the concept of a derivative by using a graphical representation of a curve and points on it. It explains how the derivative at a point is the slope of the tangent line to the curve at that point and how to calculate it using limits.
What is the derivative of the function f(x) = 5x + 3?
-The derivative of the function f(x) = 5x + 3 is f'(x) = 5, which represents the constant slope of the line.
In the context of the script, what does the derivative represent in real-world scenarios?
-In real-world scenarios, the derivative can represent various rates of change. For instance, the derivative of a position function represents velocity, and the derivative of velocity represents acceleration.
How does the script differentiate between calculating the slope of a line and the slope of the tangent line to a curve?
-The script differentiates by explaining that the slope of a line is calculated using two points on the line, while the slope of the tangent line to a curve at a specific point is found by taking the limit as the distance between two points on the curve approaches zero, thus finding the instantaneous rate of change at that point.

Outlines

00:00

📚 Introduction to Derivatives

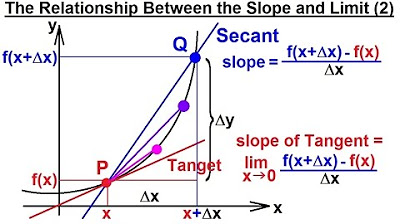
The video script begins with an introduction to derivatives, explaining that they may seem confusing at first but will become clear through the explanation. The concept is introduced using a graphical representation, with a point P on a graph and another point A+H along the x-axis. The goal is to define the derivative of the curve at point P, which is the slope of the line tangent to the curve at that point. The general formula for the slope of a line is also discussed, which is the rise over run (Y2 - Y1) / (X2 - X1). The explanation sets the stage for a deeper understanding of derivatives and their calculation.

05:03

📈 Calculating the Slope of a Line

This paragraph delves into the specifics of calculating the slope of a line using the formula derived from the rise over run concept. The focus is on understanding the slope of a line passing through two points on a curve, and how this relates to finding the derivative of the curve at a specific point. The explanation clarifies the difference between the slope of a line through two points and the slope of the tangent line to the curve at a point. The concept of limits is introduced as a fundamental part of calculus, explaining how it allows for the calculation of the derivative as H approaches zero, which simplifies to the slope of the tangent line.

10:04

🔢 Derivative Calculation and Limit Concept

The paragraph explains the process of calculating the derivative of a function at a specific point, using the limit as H approaches zero. It provides a step-by-step algebraic breakdown of the derivative calculation for a function P(T) = t^2 - 6T - 5, with the derivative evaluated at the point T=2. The explanation simplifies the algebraic expression and applies the concept of limits to arrive at the final answer for the derivative. This paragraph emphasizes the importance of understanding the limit concept in calculus and its application in derivative calculations.

15:05

📊 Simplifying Derivative Expressions

This section continues the discussion on derivatives, focusing on simplifying the expressions and evaluating them at specific points. Two examples are provided: one where the derivative is evaluated at a point (for the function P(x) = x^2 - 6x - 5), and another where the derivative is expressed as a function of x (for the function f(x) = 5x + 3). The explanations detail the algebraic steps required to simplify and evaluate the derivatives, leading to the final results. The paragraph reinforces the idea that while the limit formula is essential for understanding the definition of a derivative, it is not used regularly in practical calculus problems.

20:07

🌟 Understanding Derivatives in Practical Terms

The final paragraph summarizes the key concepts introduced in the script, emphasizing the practical understanding of derivatives. It explains that derivatives represent the slope of a line or tangent to a curve at a point, and can be thought of as rates of change. The analogy of position function to velocity and velocity to acceleration is used to illustrate the concept. The paragraph concludes by highlighting the importance of learning to calculate derivatives for various functions and applying them to solve real-world problems.

Mindmap

Keywords

💡Derivative

The derivative is a fundamental concept in calculus that represents the rate of change or the slope of a curve at a specific point. In the context of the video, it is introduced as the slope of the line tangent to a curve at a given point P, which is used to understand how the function changes at that point. The video explains the derivative using the limit process, where the difference quotient is taken as H approaches zero, which gives the instantaneous rate of change at point P.

💡Limit

In mathematics, a limit is a value that a function or sequence approaches as the input (or index) approaches some value. In the video, the concept of a limit is used to define the derivative, where the limit of a ratio of differences (rise over run) as H approaches zero gives the instantaneous rate of change or the slope of the tangent line to the curve at point P. The limit is a fundamental concept that allows us to deal with the behavior of functions as they approach certain values, which is crucial in understanding derivatives and their applications.

💡Slope

Slope is a measure of the steepness of a line, representing the rate of change of the y-values with respect to the x-values. In the video, the slope is used to describe the tangent line to a curve at a specific point, which is the same as the derivative of the function at that point. The slope is a key concept in understanding how the function changes or 'slopes' at different points along its graph.

💡Function

A function is a mathematical relation that pairs each element from a set (called the domain) to a unique element in another set (called the codomain). In the video, functions are used to represent mathematical relationships, and the focus is on understanding how these relationships change, as indicated by their derivatives. Functions are the core of the discussion, as the derivative is a function that describes the rate of change of the original function.

💡Curve

A curve is a continuous set of points on a plane, defined by a function. In the video, curves are used to visualize the behavior of mathematical functions, and the concept of a derivative is introduced to understand the rate of change of these curves at specific points. The curve serves as a visual representation of the function, allowing for the geometric interpretation of the derivative as the slope of the tangent line.

💡Tangent Line

A tangent line is a line that touches a curve at a single point without crossing it. In the context of the video, the tangent line is used to visualize the concept of the derivative, as the slope of the tangent line at a point on a curve is equal to the derivative of the function at that point. The tangent line is a key concept for understanding how the function changes at a specific location on the curve.

💡Point P

In the context of the video, Point P refers to a specific location on a graph or curve where the derivative is being evaluated. The x-value of Point P is denoted as 'a', and the video discusses finding the derivative, or the slope of the tangent line, at this point. Point P is essential for understanding the local behavior of the function, as the derivative at P gives the instantaneous rate of change at that location.

💡Rise Over Run

The phrase 'rise over run' refers to the basic method of calculating the slope of a line, which is the change in the y-values (rise) divided by the change in the x-values (run). In the video, this concept is used to explain the general idea of slope before introducing the more complex concept of derivatives. The rise over run method is a fundamental principle in understanding the steepness and direction of a line.

💡Difference Quotient

The difference quotient is a formula used in calculus to approximate the derivative of a function. It is the ratio of the difference in y-values of two points on a function to the difference in their x-values. In the video, the difference quotient is the foundation for defining the derivative, and it is used to find the slope of the tangent line at a point on a curve as H (the difference in x-values) approaches zero.

💡Instantaneous Rate of Change

The instantaneous rate of change is the derivative's value at a specific point, representing the rate at which a function changes at that very moment. It is a key concept in understanding how a function behaves locally, providing the exact slope of the tangent line at a given point on the curve. The instantaneous rate of change is what the derivative quantifies, allowing us to understand the function's behavior more precisely.

💡Algebra

Algebra is a branch of mathematics that uses symbols and rules to solve equations and problems. In the video, algebra is used to simplify and calculate the derivative of functions, demonstrating how algebraic manipulation can help understand and find the slope of a tangent line at a point on a curve. Algebraic techniques are essential for working with the formulas and equations involved in calculus, such as the difference quotient and the limit process.

Highlights

Derivative is defined as the slope of the line tangent to a curve at a specific point.

The general formula for the slope of a line is rise over run, or (y2 - y1) / (x2 - x1).

To find the derivative, we calculate the slope of a line through two points on the curve and then take the limit as the distance between these points approaches zero.

The limit is a fundamental concept in calculus, representing the value that a function approaches as a variable approaches a certain number.

The derivative of a function at a specific point 'a' is given by the limit (as h approaches 0) of [f(a + h) - f(a)] / h.

In practical terms, the derivative can be thought of as the rate of change or velocity in the context of motion, and acceleration when considering the derivative of velocity.

The process of finding the derivative involves plugging in values into the function, simplifying expressions, and applying the concept of limits.

For a function f(x) = 5x + 3, the derivative f'(x) is simply 5, representing a constant slope throughout the entire line.

The derivative of a position function represents velocity, and the derivative of velocity represents acceleration.

Understanding the concept of derivatives is crucial for solving problems in calculus and understanding the rate at which a function changes.

The lecture provides a clear and straightforward explanation of derivatives, making the concept accessible to learners.

The process of finding the derivative involves taking the difference in y-values and dividing by the difference in x-values between two points on the curve.

The concept of the limit is used to find the exact slope of the tangent line by shrinking the distance between the two points on the curve to zero.

The lecture emphasizes that while the limit formula for derivatives is fundamental, it is not used regularly in practical calculus problems.

The lecture demonstrates the calculation of derivatives through two example problems, providing a clear application of the theoretical concepts.

The derivative provides a way to analyze the behavior of a function at any point, offering insights into how the function changes as the input variable changes.

Transcripts

Browse More Related Video

Definition of the Derivative Review

Definition of the Derivative

Definition of the Derivative | Part I

How to Find the Equation of a Tangent Line

How To Find The Equation of a Tangent Line Using Derivatives - Calculus 1

Calculus 1: Limits & Derivatives (4 of 27) The Relationship Between the Slope and the Limit (2)

Related Tags

Derivatives Calculus Slope Rate of Change Limits Functions Algebra Math Education Tangents Motion Analysis