Calculus 1: Limits & Derivatives (4 of 27) The Relationship Between the Slope and the Limit (2)

Michel van Biezen
23 Aug 201506:04
EducationalLearning
32 Likes 10 Comments

TLDRThis online lecture explores the relationship between slope and limits, focusing on the concept of tangent lines and secant lines in the context of a function on the XY plane. It demonstrates how the slope of a secant line approximates the slope of a tangent line and the function at a specific point by bringing point Q closer to point P. The lecture culminates in the mathematical expression of this process using limits, illustrating how the limit as Ξ”X approaches zero defines the slope of the tangent line, which is also the derivative of the function at point P. This fundamental concept is key to understanding derivatives in calculus.

Takeaways
  • πŸ“š The lecture discusses the relationship between slope, limit, and derivatives in calculus.
  • πŸ“ˆ The slope of a tangent line is defined as the instantaneous rate of change at a specific point on a function.
  • πŸ“ A tangent line touches the graph of a function at exactly one point, Point P.
  • πŸ“‰ A secant line passes through Point P and another point, Point Q, on the graph of the function.
  • πŸ” The slope of the secant line approximates the slope of the tangent line but is not exact.
  • βž— The slope of the secant line is calculated by the ratio of the rise over the run between points P and Q.
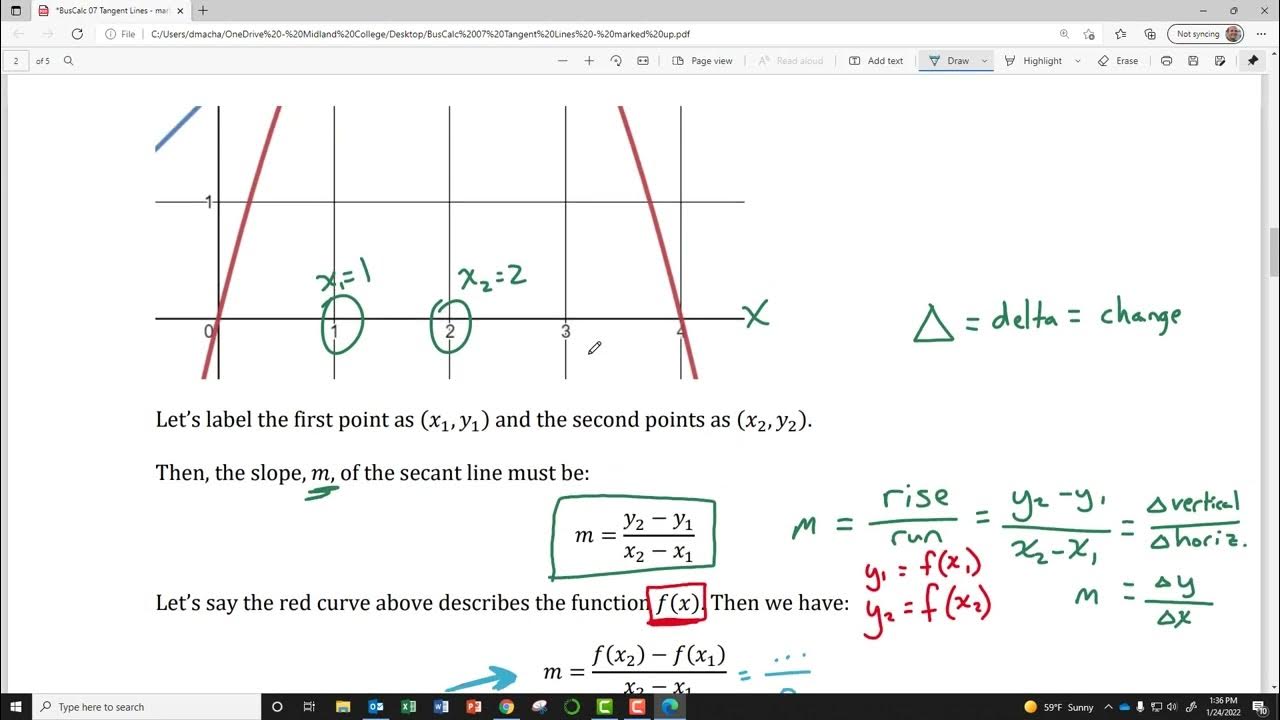
  • πŸ“ The rise is the difference in y-coordinates (f(X + Ξ”X) - f(X)), and the run is the change in x-coordinates (Ξ”X).
  • πŸ”‘ As Point Q is moved closer to Point P, the slope of the secant line more closely matches the slope of the tangent line.
  • πŸš€ The concept of a limit is introduced as the process of bringing Point Q infinitely close to Point P, making Ξ”X approach zero.
  • 🌟 In the limit, as Ξ”X approaches zero, the slope of the secant line converges to the slope of the tangent line, which is the derivative of the function at Point P.
  • πŸ”¬ The limit is a fundamental concept in calculus that helps in understanding derivatives and their applications.
Q & A

  • What is the primary focus of the lecture?

    -The lecture focuses on the relationship between the slope of a tangent line and the concept of a limit, and how to write a limit in the context of calculus.

  • What is the definition of a tangent line as described in the lecture?

    -A tangent line is defined as a line that touches the graph of a function at a single point, Point P, and does not intersect the graph at any other point.

  • What is the purpose of drawing a secant line in this context?

    -The secant line is drawn to approximate the slope of the tangent line. It passes through Point P and another point, Point Q, on the function, and as Point Q is moved closer to Point P, the slope of the secant line more closely approximates the slope of the tangent line.

  • How is the slope of the secant line defined in the lecture?

    -The slope of the secant line is defined as the ratio of the rise (change in Y values between Point Q and Point P) to the run (change in X values, which is Delta X).

  • What does the 'rise' in the context of the secant line represent?

    -The 'rise' represents the vertical distance or the change in the Y values between Point Q and Point P, which is calculated as f(X + Delta X) - f(X).

  • What is the mathematical expression for the slope of the secant line?

    -The slope of the secant line is expressed as (f(X + Delta X) - f(X)) / Delta X, where Delta X is a small change in the X coordinate.

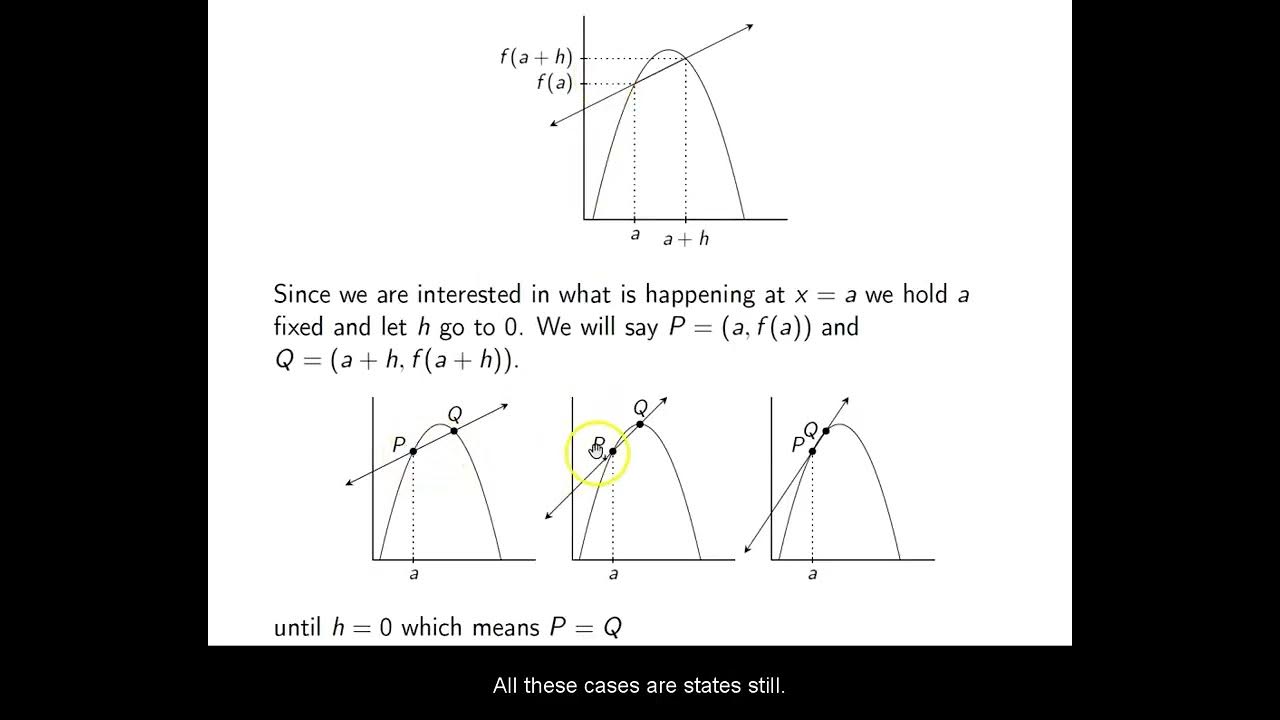
  • How does bringing Point Q closer to Point P affect the slope of the secant line?

    -Bringing Point Q closer to Point P makes the slope of the secant line more closely resemble the slope of the tangent line, thus providing a better approximation of the function's slope at Point P.

  • What is the significance of the limit in the context of finding the slope of the tangent line?

    -The limit is used to find the exact slope of the tangent line by making Delta X approach zero, which means Point Q is brought extremely close to Point P, making the secant line's slope equal to the tangent line's slope.

  • How is the limit mathematically represented in the lecture?

    -The limit is represented as the expression (f(X + Delta X) - f(X)) / Delta X as Delta X approaches zero, denoted by the limit symbol and the arrow indicating Delta X approaching zero.

  • What is the connection between the concept of the limit and derivatives in calculus?

    -The concept of the limit is fundamental to understanding derivatives. The derivative of a function at a point is found by taking the limit of the function's slope as the change in X approaches zero.

  • Why are limits important in various situations in calculus?

    -Limits are important because they help in understanding the behavior of functions as inputs approach certain values, which is essential for finding derivatives, among other applications in calculus.

Outlines
00:00
πŸ“š Understanding Slope, Limit, and Tangent Line

This paragraph introduces the concept of the relationship between the slope of a tangent line and the limit in calculus. It explains how a tangent line touches a function at a single point, P, while a secant line passes through point P and another point, Q. The slope of the secant line is shown to approximate the slope of the function at point P, and this approximation improves as point Q is moved closer to point P. The mathematical expression for the slope of the secant line is derived using the rise over run concept, with rise being the difference in y-values (f(X + Ξ”X) - f(X)) and run being the change in x-values (Ξ”X). The paragraph concludes by illustrating how, in the limit as Ξ”X approaches zero, the slope of the secant line converges to the slope of the tangent line, which is the derivative of the function at point P.

05:01
πŸ” The Role of Limits in Derivatives

The second paragraph delves deeper into the concept of limits and their significance in calculus, particularly in relation to derivatives. It emphasizes the process of approximating the slope of the tangent line by moving point Q closer to point P, which refines the approximation of the slope of the secant line. The paragraph clarifies that in the limit, as Ξ”X approaches zero, the ratio of rise over run converges to the slope of the tangent line, thereby defining the derivative of the function at point P. This concept is highlighted as fundamental in calculus, with the understanding of limits being crucial for grasping the idea of derivatives. The paragraph also hints at the broader applications of limits in various mathematical contexts, promising further exploration in upcoming videos.

Mindmap
Keywords
πŸ’‘Slope
Slope is a fundamental concept in the video, referring to the steepness or incline of a line. It is defined as the ratio of the vertical change (rise) to the horizontal change (run) between two points on a line. In the context of the video, the slope of the tangent line at a point on a function represents the instantaneous rate of change of the function at that point, which is a key concept in calculus.
πŸ’‘Limit
The limit is a central concept in calculus that describes the value that a function or sequence 'approaches' as the input or index approaches some value. In the video, the concept of a limit is used to define the slope of the tangent line to a curve at a given point, which is done by taking the limit of the secant line's slope as the two points on the curve come infinitely close together.
πŸ’‘Tangent Line
A tangent line is a straight line that touches a curve at a single point without crossing it. In the script, the tangent line is used to illustrate the concept of the derivative, which is the rate of change of a function at a particular point. The slope of the tangent line at a point on the curve is the same as the slope of the function at that point.
πŸ’‘Secant Line
A secant line is a straight line that intersects a curve at two or more points. In the video, the secant line is used to approximate the slope of the tangent line. As the points defining the secant line get closer together, its slope more closely approximates the slope of the tangent line at the point of tangency.
πŸ’‘Function
In mathematics, a function is a relation between a set of inputs and a set of permissible outputs with the property that each input is related to exactly one output. In the video, the function is represented graphically on the XY plane, and the focus is on understanding the rate of change of the function at specific points, which is done through the concept of the slope of the tangent line.
πŸ’‘Point P
Point P is a specific point on the function's graph where the tangent line is drawn. The script discusses calculating the slope at this point by using the concept of a limit, which involves bringing another point (Point Q) closer and closer to Point P to make the secant line's slope approximate the slope of the tangent line at Point P.
πŸ’‘Point Q
Point Q is another point on the function's graph, used in conjunction with Point P to form a secant line. The script explains that by moving Point Q closer to Point P, the slope of the secant line becomes a better approximation of the slope of the tangent line at Point P, illustrating the process of taking a limit.
πŸ’‘Rise
Rise refers to the vertical distance between two points on a line or curve. In the context of the video, the rise is the change in the y-values between Point P and Point Q, which is used in the calculation of the slope of the secant line.
πŸ’‘Run
Run is the horizontal distance between two points, often used in the context of calculating slope. In the video, the run is the change in the x-values between Point P and Point Q, which, along with the rise, is used to find the slope of the secant line.
πŸ’‘Delta X (Ξ”x)
Delta X, often denoted as Ξ”x, represents a small change in the x-coordinate in the function's domain. In the video, Ξ”x is used to describe the horizontal distance between Point P and Point Q. As Ξ”x approaches zero, the slope of the secant line approaches the slope of the tangent line, illustrating the concept of the limit.
πŸ’‘Derivative
A derivative in calculus is a measure of how a function changes as its input changes. The video connects the concept of the limit to the derivative by showing that the slope of the tangent line, which is the derivative, can be found by taking the limit of the secant line's slope as the points defining the secant line come together.
Highlights

The lecture discusses the relationship between slope, limit, and derivatives in calculus.

Introduction to the concept of a tangent line touching the graph of a function at a single point.

Secant line is defined as a line that passes through two points on the function's graph, including point P.

The slope of the secant line approximates the slope at point P but is not exact.

The slope of the tangent line equals the slope of the function at the point of tangency.

To calculate the slope at point P, one can use the slope of the secant line as an approximation.

Moving point Q closer to point P refines the approximation of the secant line's slope to the function's slope at P.

The slope of the secant line is defined as the ratio of the rise over the run between points P and Q.

Rise is the difference in Y values between points Q and P, and run is the change in X values.

The change in Y values is represented by the function evaluated at X plus Delta X minus the function evaluated at X.

As Delta X approaches zero, the slope of the secant line approaches the slope of the tangent line.

The limit concept is used to describe the process of bringing points P and Q extremely close together.

The mathematical notation for the limit as Delta X approaches zero is introduced.

The limit of the rise over run as Delta X approaches zero equals the slope of the tangent line.

The slope of the tangent line is equal to the derivative of the function at point P.

The concept of the limit is fundamental to understanding derivatives in calculus.

The lecture will cover various applications of limits in future videos.

Transcripts

Browse More Related Video

Definition of the Derivative | Part I

BusCalc 07 Tangent Lines

Definition of the Derivative

Ch. 13.3 Tangent Lines and Derivatives

1.4 - Differentiation Using Limits of Difference Quotients

The Tangent Line and the Derivative (Calculus)

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus ConceptsSlope AnalysisLimit DefinitionTangent LineSecant LineFunction SlopeDerivative BasicsMath EducationOnline LectureEducational ContentMathematics Tutorial