Definition of the Derivative | Part I
TLDRThe video script introduces the concept of the derivative with a focus on the geometric interpretation of finding the slope of the tangent line at a specific point on a curve. The presenter uses a red function curve and a point 'A' with a height of 'F(a)' to illustrate the idea. The tangent line is described as the line that just touches the curve at point 'A' without crossing it. To calculate the slope of this tangent line, the script introduces the concept of a secant line, which connects point 'A' and a nearby point 'A+h'. The slope of the secant line is calculated using the rise over run method, and the presenter suggests that as 'h' approaches zero, the secant line becomes a better approximation of the tangent line. The derivative, or the slope of the tangent line at point 'A', is then defined as the limit of the secant line's slope as 'h' approaches zero. This is expressed algebraically and denoted as 'F' prime of 'a', symbolizing the derivative of the function 'F' at the point 'a'.
Takeaways
- 📐 The concept of a derivative is introduced as a foundational concept in calculus, focusing on the slope of the tangent line to a curve at a given point.
- 🔍 The tangent line is described as touching the curve at a point without crossing it, implying a very small angle between the curve and the line.
- 📈 To find the slope of the tangent line, a geometric approach is used, where an additional point `a + h` is introduced to form a secant line that approximates the tangent line as `h` approaches zero.
- 🔢 The slope of the secant line is calculated using the rise (`f(a + h) - f(a)`) over the run (`(a + h) - a`), which simplifies to `f(a + h) - f(a) / h`.
- 🎯 The process of taking the limit as `h` approaches zero is central to finding the derivative, which is the precise slope of the tangent line at point `a`.
- 📉 As `h` becomes very small, the secant line becomes an increasingly better approximation of the tangent line, visually demonstrated by moving the point `a + h` closer to `a`.
- 🧮 The derivative is defined as the limit of the slope of the secant line as `h` approaches zero, symbolized by `f'(a)` or `F'(a)`, which represents the instantaneous rate of change of the function at `a`.
- 📌 The geometric interpretation of the derivative is that it gives the slope of the tangent line to the curve at the point `a`.
- 📘 The algebraic expression for the derivative is the limit of `(f(a + h) - f(a)) / h` as `h` approaches zero.
- 📚 The script emphasizes the importance of understanding both the geometric and algebraic perspectives when dealing with derivatives.
- 🚀 The concept of the derivative is fundamental to calculus and is used to analyze rates of change and slopes of curves in various mathematical and real-world applications.
Q & A
What is the primary goal of the video?
-The primary goal of the video is to introduce the concept of a derivative, specifically focusing on understanding the slope of the tangent line at a particular point on a curve.
How does the video define the tangent line?
-The video defines the tangent line as a line that just touches the curve at a particular point without crossing it, having the same angle on both sides, and laying as flat as possible at that point.
What is the role of the point 'a plus h' in the explanation?
-The point 'a plus h' is used to create a secant line that connects this point with the point 'a' on the curve. As 'h' becomes very small, the secant line serves as an approximation for the tangent line.
How is the slope of the secant line calculated?
-The slope of the secant line is calculated by taking the rise (change in the function's value from F(a) to F(a+h)) divided by the run (change in the x-value from a to a+h).
What is the significance of taking the limit as h approaches zero?
-Taking the limit as h approaches zero allows for the approximation of the secant line to become more precise, effectively defining the slope of the tangent line at point 'a'.
What does the term 'derivative' represent in the context of the video?
-In the context of the video, the term 'derivative' represents the slope of the tangent line at a specific point on a curve, which is found by taking the limit of the slope of the secant line as the distance between the points approaches zero.
How does the video use the concept of a limit to define the derivative?
-The video uses the concept of a limit by showing that as the distance 'h' between two points on the curve approaches zero, the slope of the secant line becomes the slope of the tangent line, thus defining the derivative.
What is the geometric interpretation of the derivative?
-Geometrically, the derivative represents the slope of the tangent line to the curve at a given point, which is the steepest rate of increase of the function at that point.
Why is it important to consider a very small value for 'h'?
-Considering a very small value for 'h' is important because it allows the secant line to closely approximate the tangent line, providing a more accurate representation of the instantaneous rate of change at point 'a'.
What is the algebraic expression for the slope of the secant line?
-The algebraic expression for the slope of the secant line is (F(a+h) - F(a)) / (a+h - a), which simplifies to (F(a+h) - F(a)) / h.
How does the video script help in understanding the concept of derivatives?
-The video script helps in understanding the concept of derivatives by using a geometric approach to illustrate the idea of a tangent line and by breaking down the process of finding the slope of the tangent line through the concept of a secant line and limits.
What does the notation 'F prime of a' represent?
-The notation 'F prime of a' (F'(a)) represents the derivative of the function F at the point 'a', which geometrically is the slope of the tangent line to the curve of the function at that point.
Outlines
📐 Introduction to Tangent Line and Derivatives
The speaker expresses excitement about introducing a fundamental concept in calculus: the definition and calculation of derivatives. They aim to explain it with a geometric perspective, focusing on finding the slope of the tangent line at a specific point on a curve. The function is represented graphically in red, and a particular point 'A' with a height 'F(a)' is chosen. The tangent line is described as the line that just touches the curve at point 'A' without intersecting it sharply. The speaker introduces the idea of adding another point 'a + h' to help approximate the tangent line using a secant line, which connects the points 'a' and 'a + h'. The slope of the secant line is calculated using the rise over run method, and the goal is to approximate the tangent line's slope by shrinking the distance 'h' between the points until it approaches zero.
🔍 Defining the Derivative and Tangent Line Slope
The speaker proceeds to define the slope of the tangent line at point 'a' using the concept of limits. They clarify that as the distance 'h' between the points 'a' and 'a + h' becomes very small, the secant line becomes an increasingly accurate approximation of the tangent line. The formula for the slope of the secant line is given as F(a + h) - F(a) divided by (a + h) - a, which simplifies to F(a + h) - F(a) / h. The limit of this expression as 'h' approaches zero is used to define the slope of the tangent line. This concept is also related to the derivative of the function at point 'a', denoted as F'(a), which geometrically represents the slope of the tangent line and algebraically is the value of the limit as 'h' approaches zero.
Mindmap
Keywords
💡Derivative
💡Tangent Line
💡Secant Line
💡Slope
💡Function
💡Limit
💡Geometric Flavor
💡Point A
💡F(a)
💡A Plus H
💡Instantaneous Rate of Change
Highlights
Introduction to the foundational concept of calculating the derivative with a geometric perspective.
Objective to understand the slope of the tangent line at a specific point on a curve.
Description of a tangent line as one that touches the curve at a point without crossing it.
Use of a second point 'a plus h' to help define the tangent line's slope.
Introduction of the secant line, a line connecting two points on a curve, as a tool for approximation.
The concept that as the distance 'h' between points decreases, the secant line becomes a better approximation of the tangent line.
Mathematical expression for the slope of the secant line using the rise/run method.
Demonstration of how the secant line's slope approaches the tangent line's slope as 'h' approaches zero.
The use of limits to formally define the slope of the tangent line as 'h' approaches zero.
Clean presentation of the derivative formula, simplifying the expression for the slope of the secant line.
Differentiation between the slope of the secant line and the slope of the tangent line using the concept of a limit.
Introduction of the notation 's prime of a' to represent the derivative of a function at a point 'a'.
Geometric interpretation of the derivative as the slope of the tangent line.
Algebraic representation of the derivative as the limit of the secant line's slope as 'h' tends to zero.
Emphasis on the practical application of derivatives in understanding the behavior of functions and curves.
Visual demonstration of how the secant line's approximation improves with smaller 'h' values.
Explanation of the derivative as a foundational tool for calculus and its importance in various fields.
The process of taking the limit as a fundamental technique in calculus for finding derivatives.
Transcripts
Browse More Related Video

Definition of the Derivative
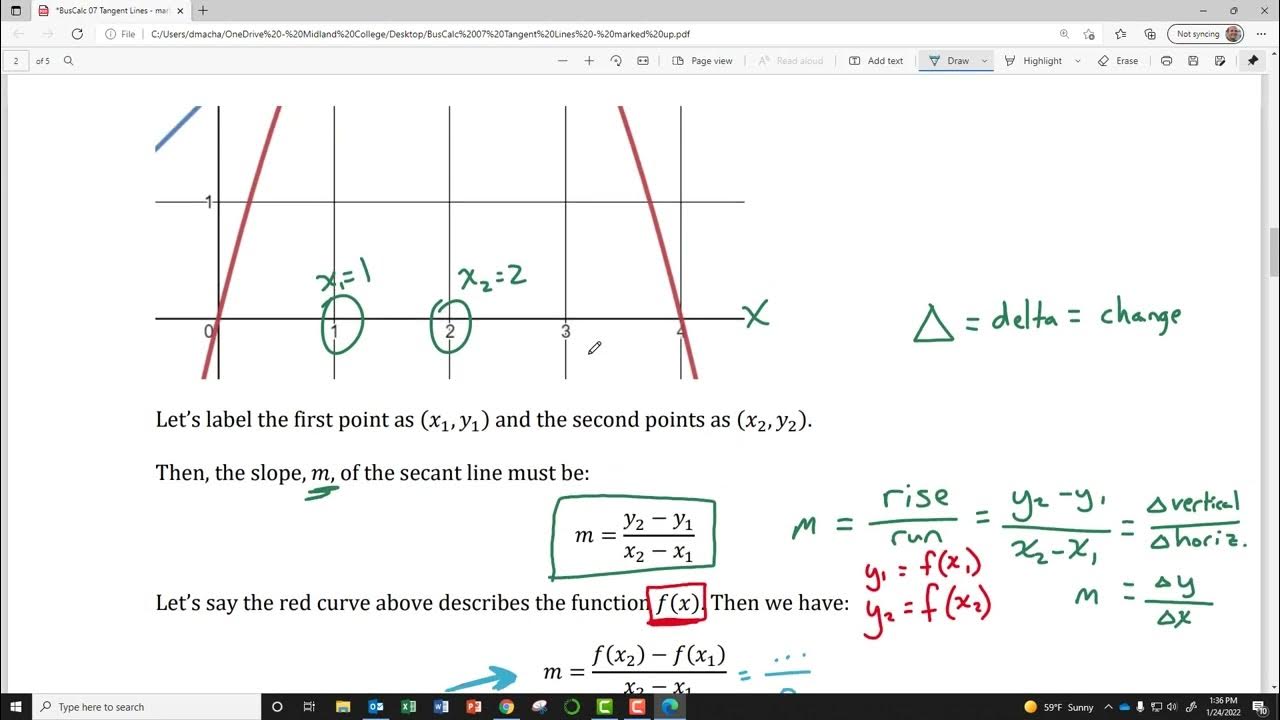
BusCalc 07 Tangent Lines
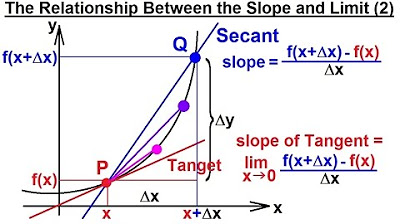
Calculus 1: Limits & Derivatives (4 of 27) The Relationship Between the Slope and the Limit (2)

Calculating slope of tangent line using derivative definition | Differential Calculus | Khan Academy

1.4 - Differentiation Using Limits of Difference Quotients

Equation of a normal line [IB Maths AI SL/HL]
5.0 / 5 (0 votes)
Thanks for rating: