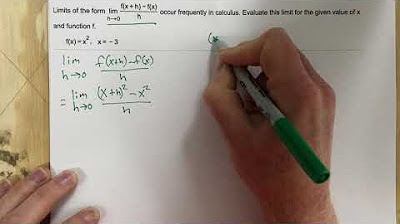Definition of the Derivative Review
TLDRThe video script provides an insightful explanation of the concept of the derivative, a fundamental concept in calculus. It begins by addressing the varying levels of understanding students may have when first introduced to the topic. The presenter then outlines two primary methods for calculating derivatives. The first method involves finding the slope of the tangent line at a specific point on a curve by taking the limit as another point approaches the point of interest. An example using the function f(x) = x^3 is given, demonstrating how to apply the definition of the derivative to find the slope at x = 3. The second method involves considering a small change in x (denoted as h or Δx) and calculating the derivative at a general point x by taking the limit as h approaches zero. An example with the function f(x) = √x is used to illustrate this process, including a step to rationalize the numerator to avoid division by zero. The script emphasizes the importance of memorizing the derivative formulas for both methods to apply them effectively in various mathematical problems.
Takeaways
- 📚 The concept of a derivative is fundamental, with varying initial understanding among students.
- 📈 The derivative represents the slope of a curve at a specific point, which can be approached through two different methods.
- 🔍 The first method involves finding the limit of the slope between two points as they converge, denoted as f'(a).
- 📌 An example is provided using f(x) = x^3 to illustrate the process of finding the derivative at a specific point, x = 3.
- 🤔 Direct substitution into the limit can lead to division by zero, which requires rethinking the approach, such as factoring or synthetic division.
- 🔑 Synthetic division is demonstrated to simplify the expression for finding the limit as x approaches 3.
- 👉 The second method for dealing with derivatives involves considering a small change in x, denoted as h or Δx, leading to a new point on the curve.
- 📝 The limit as h approaches zero of the difference quotient is used to define the derivative at a general point, f'(x).
- 🌟 Rationalization of the numerator is a technique used to avoid the indeterminate form 0/0 when taking limits.
- ✅ An example using f(x) = √x is given to show how to find the derivative using the limit as h approaches zero.
- 💡 Memorizing the process and formulas is emphasized for ease of application when needed.
- ✨ Understanding both ways of defining the derivative is crucial for applying it to various mathematical problems.
Q & A
What is the definition of a derivative?
-The derivative of a function at a certain point is the slope of the tangent line to the graph of the function at that point. It can be found using the limit of the slope between a point on the curve and another point as the latter approaches the former.
How do you find the derivative of a function at a specific point using the limit definition?
-You calculate the slope between the point (a, f(a)) and another point (x, f(x)) on the curve, and then take the limit as x approaches a, which is denoted as f'(a) = lim (x -> a) [(f(x) - f(a))/(x - a)].
What is the notation used to represent the derivative of a function?
-The derivative is represented as f'(x) or df/dx, which signifies the rate of change of the function with respect to x.
How can you deal with the indeterminate form 0/0 when finding a derivative?
-You can deal with the indeterminate form 0/0 by algebraically simplifying the expression before taking the limit, or by using techniques like synthetic division to simplify the expression before substituting the value.
What is the alternative method to find the derivative of a function?
-The alternative method involves considering a small change in x, denoted as h or Δx, and finding the limit as h approaches zero of the expression [(f(x + h) - f(x))/h], which gives f'(x).
How do you rationalize the numerator when taking a limit as h approaches zero?
-You multiply the numerator and the denominator by the conjugate of the numerator to eliminate the square root in the denominator, which allows you to simplify and substitute h = 0 without encountering division by zero.
What is the derivative of the function f(x) = x^3 at the point x = 3?
-Using the limit definition, the derivative f'(3) is found by taking the limit as x approaches 3 of [(x^3 - 3^3)/(x - 3)]. After simplification and substitution, the derivative is 27.
What is the process of synthetic division and how is it used in finding derivatives?
-Synthetic division is a method used to divide a polynomial by a linear binomial of the form (x - a). It is used in finding derivatives to simplify expressions, especially when dealing with polynomial functions, by dividing the polynomial by (x - a) to find the depressed equation.
Why is it important to memorize the definition of the derivative and its notation?
-Memorizing the definition and notation of the derivative is important because it allows you to apply the concept correctly and efficiently in various mathematical problems and calculations, without having to re-derive it each time.
What is the derivative of the function f(x) = √x?
-The derivative f'(x) is found by taking the limit as h approaches zero of [(√(x + h) - √x)/h]. After rationalizing the numerator and simplifying, the derivative is 1/(2√x).
How does the concept of limits play a crucial role in understanding derivatives?
-Limits are crucial in understanding derivatives because they allow us to find the instantaneous rate of change of a function at a specific point, which is the definition of the derivative. Limits help us to approach a value without actually reaching it, which is essential for defining the derivative at a point.
What are the two primary ways of using the definition of the derivative as described in the script?
-The two primary ways are: 1) Using the limit as x approaches a to find the derivative at a specific point a on the curve, and 2) Using the limit as h approaches zero to find the derivative at a point x on the curve, considering a small change h in the x-value.
Outlines
📈 Understanding Derivatives Through Limit of a Slope
The first paragraph introduces the concept of a derivative as the slope of a curve at a given point. The speaker uses a graph of a function F(x) to illustrate the process of finding the derivative at a specific point 'a'. They explain the two-point approach where the slope between two points, one approaching the other, is calculated as (f(x) - F(a)) / (x - a). The limit of this slope as x approaches a is the derivative, denoted as f'(a). An example is provided to find the derivative of F(x) = x^3 at x = 3, which involves algebraic simplification and synthetic division to avoid division by zero. The process concludes with the evaluation of the limit as x approaches 3, resulting in the derivative of the function at that point.
🔄 Applying the Derivative Definition with Incremental Change
The second paragraph discusses an alternative method for finding derivatives, which involves considering a small change in the input, denoted as 'h' or Δx. The speaker describes moving from a point x to a new point x + h on the curve and finding the derivative at x, denoted as f'(x). This is done by taking the limit as h approaches zero of the difference quotient [F(x + h) - F(x)] / h. An example is given using F(x) = √x, where the limit as h approaches zero of the expression √(x + h) - √x / h is evaluated. The speaker demonstrates how to rationalize the numerator to avoid the indeterminate form 0/0, leading to a simplified expression that can be evaluated as h approaches zero, resulting in the derivative of the function at x.
Mindmap
Keywords
💡Derivative
💡Limit
💡Slope
💡Graph
💡Function
💡Cubed
💡Synthetic Division
💡Rationalize the Numerator
💡Conjugate
💡Delta X (or H)
💡Square Root Function
Highlights
The importance of understanding the definition of the derivative is emphasized, as it is a fundamental concept with varying levels of initial comprehension.
Two different methods for using derivatives are introduced: finding the slope at a specific point and the general derivative function.
The concept of the derivative as the slope at a point on a curve is explained, with a demonstration using a graph of f(x).
The limit definition of the derivative is introduced, where x approaches a, and the slope between two points is considered.
The notation f'(a) is used to represent the derivative, and the limit process is explained in detail.
An example is given to illustrate the process of finding the derivative of f(x) = x^3 at the point x = 3.
The use of synthetic division to simplify the expression for the derivative is demonstrated.
The concept of a limit is discussed, particularly when dealing with expressions that could result in division by zero.
The second method for dealing with derivatives involves a point x, a function f(x), and a movement along the curve defined by a distance H.
The limit as H approaches zero is used to find the derivative f'(x), which is the general derivative function.
The process of rationalizing the numerator to avoid division by zero when taking the limit is explained.
An example using f(x) = √x to find the derivative f'(x) is provided, showcasing the limit process and rationalization technique.
The final answer for the derivative of √x is presented as 1/(2√x), demonstrating the successful application of the limit definition.
The necessity of memorizing the limit definition of the derivative for its practical application in calculus is stressed.
The importance of understanding both methods of finding derivatives is highlighted for versatility in problem-solving.
The transcript concludes with a wish for the audience's success in grasping the concept of derivatives.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: