Cross Product of Two Vectors Explained!
TLDRThe video script offers a detailed explanation of how to calculate the cross product of two vectors. It begins by defining the cross product and provides an example using vectors A and B with their respective components. The process involves representing the vectors as a 3x3 matrix and calculating the determinant to find the components of the resulting vector, which is perpendicular to the original vectors. The script further explains how to verify the correctness of the cross product using the dot product, ensuring that the new vector is orthogonal to the original ones. An additional example reinforces the method, highlighting the steps and calculations involved.
Takeaways
- 🧮 The cross product of two vectors results in a third vector perpendicular to the original pair.
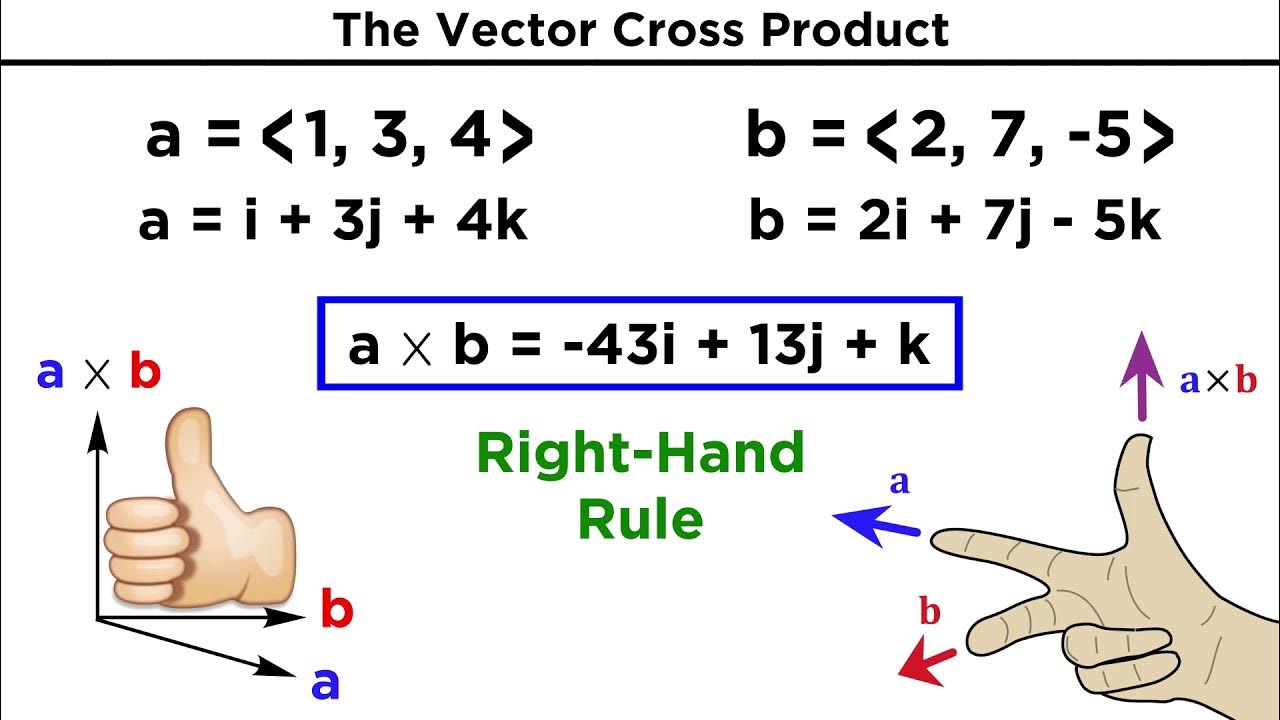
- 📐 To compute the cross product, represent the vectors in a 3x3 matrix with i, j, k unit vectors on the top row, and the components of the two vectors in the subsequent rows.
- 🔢 Finding the cross product involves calculating the determinant of the 3x3 matrix, resulting in a new vector expressed in terms of i, j, k.
- ✂️ The determinant of a 2x2 matrix, crucial for computing the cross product, is found by multiplying the diagonal elements and then subtracting the products.
- 📉 The components of the resulting vector from the cross product can have positive or negative values, indicating the direction of the vector.
- ✔️ Verification of the correctness of a cross product can be done by checking if the resulting vector is orthogonal to the original vectors using the dot product.
- 🔍 The dot product of two orthogonal vectors is zero, a property used to confirm the cross product's accuracy.
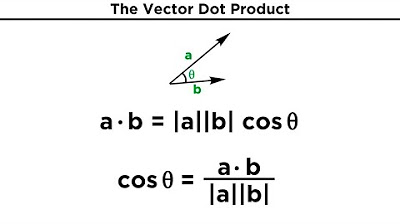
- 📚 The formula for the dot product involves multiplying corresponding components of two vectors and summing these products.
- 🔄 The script provides a detailed, step-by-step example of calculating the cross product and verifying it using the dot product.
- 👩🏫 Understanding cross and dot products is essential for solving problems involving vector perpendicularity and orthogonality.
Q & A
What is the cross product of two vectors?
-The cross product of two vectors is a vector that is perpendicular to both input vectors and follows the right-hand rule in terms of direction. It can be calculated using the determinant of a 3x3 matrix formed by the unit vectors (i, j, k) and the components of the two input vectors.
How do you represent vector a in the given example?
-In the given example, vector a is represented as 3i + 5j - 7k, which corresponds to its components along the x, y, and z axes.
What is the matrix form used to calculate the cross product?
-The matrix form used to calculate the cross product involves placing the unit vectors (i, j, k) in the first row, followed by the components of the first vector in the second row and the components of the second vector in the third row.
How do you find the determinant of a 2x2 matrix?
-The determinant of a 2x2 matrix (a b; c d) is found by calculating the product of a and d, minus the product of b and c (ad - bc).
What is the resulting vector after calculating the cross product of vectors a and b in the example?
-The resulting vector after calculating the cross product of vectors a (3i + 5j - 7k) and b (2i - 6j + 4k) is -22i - 26j - 28k.
How can you verify if the cross product is calculated correctly?
-To verify the cross product, you can check if the dot product of the resulting vector (cross product) with each of the original vectors is zero. If both dot products are zero, it indicates that the new vector is orthogonal (perpendicular) to the original vectors, confirming the correctness of the cross product.
What is the significance of the right-hand rule in vector operations?
-The right-hand rule is used to determine the direction of the cross product of two vectors. It states that if you point your right-hand fingers in the direction of the first vector and curl them towards the second vector, your thumb will point in the direction of the cross product.
What are the components of vector b in the example?
-In the given example, vector b is represented as 2i - 6j + 4k, which are its components along the x, y, and z axes.
How do you calculate the cross product for another set of vectors, say a (5, -4, 3) and b (-7, -8, 0)?
-To calculate the cross product for vectors a (5, -4, 3) and b (-7, -8, 0), you set up a 3x3 matrix with the unit vectors (i, j, k) and the components of vectors a and b. Then, you calculate the determinants of the resulting 2x2 matrices for each component of the cross product, following the same process as in the initial example.
What is the resulting vector from the cross product of the second set of vectors a (5, -4, 3) and b (-7, -8, 0)?
-The resulting vector from the cross product of vectors a (5, -4, 3) and b (-7, -8, 0) is 26i + 19j - 18k.
How do you confirm that the cross product of the second set of vectors is correct?
-To confirm the correctness of the cross product for the second set of vectors, you calculate the dot products of the resulting vector with both original vectors and check if they are equal to zero. If both dot products are zero, it confirms that the vectors are orthogonal, and thus, the cross product is correct.
What is the relationship between the cross product and the dot product of vectors?
-The cross product results in a vector that is orthogonal to the two input vectors, while the dot product of two vectors can indicate whether they are orthogonal (if the dot product is zero). The cross product is sensitive to the orientation of the vectors in three-dimensional space, whereas the dot product reflects the relative direction and magnitude of the vectors.
Outlines
📚 Introduction to Cross Product Calculation
This paragraph introduces the concept of finding the cross product of two vectors. It explains the process of calculating the cross product by using a matrix method and provides an example with vectors a = 3i + 5j - 7k and b = 2i - 6j + 4k. The explanation includes placing the vectors in a 3x3 matrix, calculating the determinants of 2x2 matrices derived from the 3x3, and combining these to find the components of the resulting cross product vector. The paragraph emphasizes the importance of verifying the result by checking the orthogonality of the cross product vector to the original vectors.
🔍 Verifying the Cross Product through Dot Product
This paragraph focuses on the verification of the calculated cross product using the dot product. It explains that the cross product of two vectors results in a new vector that is perpendicular to both original vectors, leading to a dot product of zero. The paragraph provides the formula for the dot product and demonstrates how to apply it to confirm the correctness of the cross product by showing that the dot products of the original vectors with the calculated cross product vector are indeed zero. It also presents another example with different vector components and guides through the cross product calculation, reinforcing the verification process.
📈 Detailed Calculation of Cross Product for Additional Vectors
The paragraph delves into a detailed calculation of the cross product for another set of vectors a = 5i - 4j + 3k and b = -7i - 8j. It outlines the step-by-step process of constructing a 3x3 matrix with the given vector components, calculating the determinants for the i, j, and k components, and assembling these to find the components of the new cross product vector. The paragraph also reiterates the verification process by calculating and confirming that the dot products of the original vectors with the new cross product vector are zero, thus validating the accuracy of the calculation.
Mindmap
Keywords
💡Cross Product
💡Vector
💡Matrix
💡Determinant
💡Orthogonal
💡Dot Product
💡Perpendicular
💡Components
💡Unit Vectors
💡Geometry
💡Linear Algebra
Highlights
The method of finding the cross product of two vectors is discussed in the video.
Vector a is represented as 3i + 5j - 7k and vector b as 2i - 6j + 4k.
The cross product is determined by using a 3x3 matrix and calculating the determinant.
The x, y, and z components of a vector correspond to the i, j, and k units respectively.
The cross product results in a new vector that is perpendicular to the original two vectors.
The determinant of a 2x2 matrix is found by multiplying the diagonal elements and subtracting the product of the off-diagonal elements.
The cross product of two vectors can be verified by checking if the dot product of the new vector with the original vectors equals zero.
A detailed example is provided to illustrate the calculation of the cross product for specific vectors.
The video explains how to evaluate the determinant of 2x2 matrices derived from the 3x3 matrix for the cross product.
The final result of the cross product is given in vector form as -22i - 26j - 28k.
The concept of perpendicularity in vector space is emphasized in relation to the cross product.
A second example is presented with different vector components to demonstrate the generality of the cross product method.
The components of the second example vectors are 5, -4, 3 for vector a and -7, -8 for vector b.
The video shows the step-by-step process of calculating the cross product for the second set of vectors.
The resulting vector from the second example is 26i + 19j - 18k.
The verification of the cross product's correctness is confirmed by calculating and showing that the dot products with the original vectors are zero.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: