Cross Product and Dot Product: Visual explanation
TLDRThis script introduces the concepts of cross and dot products in vector mathematics. It explains that the cross product of two vectors results in a third vector perpendicular to the original pair, with a magnitude equal to the area of the parallelogram formed by the two vectors. The dot product, on the other hand, yields a scalar value based on the product of the magnitudes and the cosine of the angle between the vectors. The script emphasizes the importance of these operations in scientific and engineering fields and provides a mnemonic using the right-hand rule to determine the direction of the cross product.
Takeaways
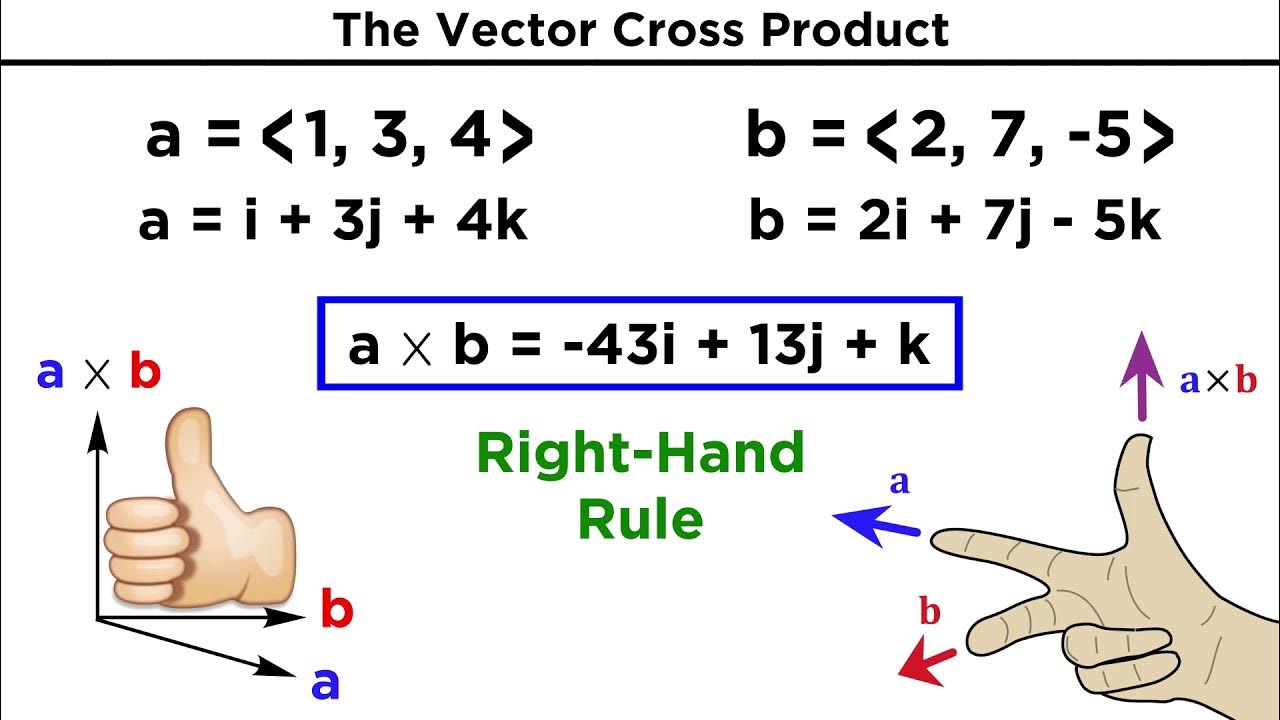
- 🔍 The cross product of two arrows is defined as a third arrow that is perpendicular to the original two.
- 📐 The length of the cross product arrow is equivalent to the area of the parallelogram formed by the two original arrows.
- 🛠️ The cross product is significant in various scientific and engineering fields.
- 🔄 The dot product of two arrows results in a scalar value, not a vector.
- 📈 The dot product is calculated by multiplying the length of one arrow by the length of the side of a triangle formed with the other arrow.
- 🔽 If two arrows are in opposite directions, the dot product is negative.
- ↔️ The result of the dot product is invariant to the order of the arrows.
- ➡️ The cross product's direction can be determined using the right-hand rule.
- 🎯 The right-hand rule states that if you point your right hand in the direction of the first arrow and curl your fingers towards the second arrow, your thumb points in the direction of the cross product.
- 📚 More detailed information on these topics can be found in other videos on the same channel.
Q & A
What is the cross product of two arrows defined as?
-The cross product of two arrows is defined as a third arrow that is always exactly 90 degrees to the two original arrows.
How is the length of the arrow representing the cross product determined?
-The length of the arrow representing the cross product is equal to the area of the parallelogram formed by the original two arrows.
In what fields is the cross product of two arrows significant?
-The cross product of two arrows plays a critical role in many areas of science and engineering.
What is the dot product of two arrows and how is it calculated?
-The dot product of two arrows is a numerical value obtained by multiplying the length of the side of the triangle formed by the two arrows by the length of the first arrow.
How does the direction of the dot product relate to the directions of the two arrows?
-If the first arrow and the second arrow are pointed in opposite directions, then the dot product is negative.
What is the main difference between the cross product and the dot product of two arrows?
-While the cross product results in another arrow, the dot product results in a scalar (a number).
Does the order of the arrows affect the result of the dot product?
-No, the dot product of two arrows will always yield the same result regardless of which arrow is considered first or second.
How does the order of the arrows affect the cross product?
-If the order of the two original arrows is reversed, the arrow for the cross product will point in the opposite direction.
What is the right-hand rule for determining the direction of the cross product?
-The right-hand rule states that if you point your right hand in the direction of the first arrow and curl your fingers in the direction of the second arrow, your thumb will point in the direction of the cross product.
What additional resources are available for learning about the cross product and dot product?
-More information on the cross product and dot product can be found in other videos on the same channel, and subscribing will provide notifications when new videos are ready.
What is the geometric interpretation of the dot product in terms of the triangle formed by the two vectors?
-The dot product can be interpreted as the product of the length of one vector and the projection of the other vector onto the first one, which corresponds to the length of the side of the triangle formed by the vectors multiplied by the length of the first vector.
How can the cross product be visualized in three-dimensional space?
-The cross product can be visualized as a vector that is perpendicular to the plane defined by the two original vectors, with its direction following the right-hand rule and its magnitude equal to the area of the parallelogram spanned by the two vectors.
Outlines
📐 Understanding the Cross and Dot Products
This paragraph introduces the concept of cross and dot products in vector mathematics. It explains that the cross product of two vectors results in a third vector that is perpendicular to the original two, with its length equivalent to the area of the parallelogram formed by the two vectors. The paragraph also contrasts this with the dot product, which is a scalar value, and highlights the importance of these operations in scientific and engineering fields. Additionally, it touches on the symmetry of the dot product and the directionality of the cross product, providing a mnemonic using the right-hand rule to remember the direction of the cross product.
Mindmap
Keywords
💡Arrows
💡Cross Product
💡Dot Product
💡Area of Parallelogram
💡Perpendicular
💡Right Hand Rule
💡Magnitude
💡Triangle
💡Direction
💡Projection
💡Scalar
Highlights
Define cross product of two arrows resulting in a third arrow.
Cross product arrow is always 90 degrees to the original arrows.
Length of cross product arrow equals the area of the parallelogram formed by the original arrows.
Cross product is crucial in various scientific and engineering fields.
Introduction to the dot product of two arrows.
Dot product involves a triangle formed by two arrows and the product of one side's length and the first arrow's length.
The dot product can be negative if the arrows are in opposite directions.
Dot product results in a numerical value, unlike the cross product which is another arrow.
The result of the dot product is consistent regardless of which arrow is considered first or second.
Cross product direction changes if the order of original arrows is reversed.
Right-hand rule to remember the direction of the cross product arrow.
Extend your thumb after pointing in the direction of the first arrow and curling fingers towards the second arrow.
Additional information available in other videos on the channel.
Subscribe for updates on new video releases.
The video content is part of a series for comprehensive understanding.
Mathematical concepts like cross and dot products are fundamental in vector analysis.
These vector operations have wide-ranging applications in physics and engineering problems.
The video provides a clear and concise explanation of cross and dot products.
The use of visual aids and analogies helps in better understanding complex concepts.
The video emphasizes the importance of vector operations in problem-solving.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: