Cross Product (Introduction)
TLDRThis video script from Houston Math Prep explores the concept of vector directions, focusing on the parallel and orthogonal directions relative to a given vector 'w'. It explains that there are two parallel directions to any vector: the same and the opposite. Meanwhile, an infinite number of orthogonal directions exist, all lying in a plane perpendicular to the vector. The script delves into the cross product, a method to find a vector orthogonal to two given vectors, using the right-hand rule and determinants of matrices. The cross product results in a vector perpendicular to the plane containing the original vectors, with the direction determined by the right-hand rule. Examples illustrate the calculation of cross products for given vectors.
Takeaways
- 📚 The script introduces the concept of parallel and orthogonal directions in relation to a given vector 'w', exemplified by the vector (1, 2, 3).
- 🔍 There are two parallel directions to any vector: one in the exact same direction and one in the exact opposite direction.
- 🔄 Parallel vectors can be any positive or negative multiple of the original vector, pointing in the same or opposite direction.
- 📉 The script explains that there are infinitely many orthogonal (perpendicular) directions to a given vector in 3D space.
- 📐 Orthogonal vectors lie in a plane that is perpendicular to the original vector, and their dot product with the original vector is zero.
- 🤔 The process of finding a vector orthogonal to two given vectors 'u' and 'v' is detailed, resulting in a formula for vector 'w'.
- 🔢 The components of the orthogonal vector 'w' are derived from the cross product of vectors 'u' and 'v'.
- 📝 The cross product is shown to be a vector that is orthogonal to the plane containing the original two vectors and is calculated using the determinant of a matrix.
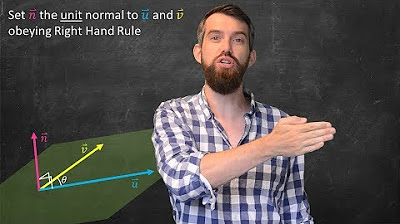
- 👉 The right-hand rule is introduced to determine the direction of the cross product, with 'u cross v' and 'v cross u' pointing in opposite directions.
- 🧠 The determinant of a 3x3 matrix is used to calculate the cross product, with the script providing a step-by-step method for expansion.
- 📚 The script concludes with examples of calculating the cross product for given vectors 'u' and 'v', demonstrating the resulting orthogonal vector.
Q & A
What is the vector w mentioned in the script?
-The vector w mentioned in the script is (1, 2, 3), which is used as an example to illustrate the concept of parallel and orthogonal directions.
How many parallel directions are there to a given vector w?
-There are infinitely many parallel directions to a given vector w. These directions are represented by all positive and negative multiples of the vector w, pointing in the same or opposite direction, respectively.
What is the relationship between the vectors listed in the script and vector w?
-The vectors listed in the script are multiples of vector w, either positive or negative, indicating different lengths but the same or opposite direction as vector w.
What does the term 'orthogonal' mean in the context of vectors?
-In the context of vectors, 'orthogonal' means being perpendicular to each other, with a dot product of zero.
How many orthogonal directions are there to a given vector w in 3D space?
-There are infinitely many orthogonal directions to a given vector w in 3D space. These directions lie in the plane that is perpendicular to vector w.
What is the significance of the dot product when dealing with orthogonal vectors?
-The dot product is significant because if two vectors are orthogonal, their dot product equals zero. This property is used to determine if vectors are perpendicular.
What is the cross product of two vectors and what does it represent?
-The cross product of two vectors is a vector that is orthogonal to both of the original vectors and lies in the plane perpendicular to them. It represents the direction and magnitude of a vector that is perpendicular to the plane formed by the two vectors being multiplied.
How does the right-hand rule relate to the cross product?
-The right-hand rule is used to determine the direction of the cross product. If you orient your right hand along the first vector and curl your fingers in the direction of the second vector, your thumb points in the direction of the cross product.
What is the determinant of a matrix used for in the context of the cross product?
-In the context of the cross product, the determinant of a matrix is used to calculate the components of the resulting vector. The matrix includes the unit vectors i, j, k in the first row and the components of the two vectors being crossed in the subsequent rows.
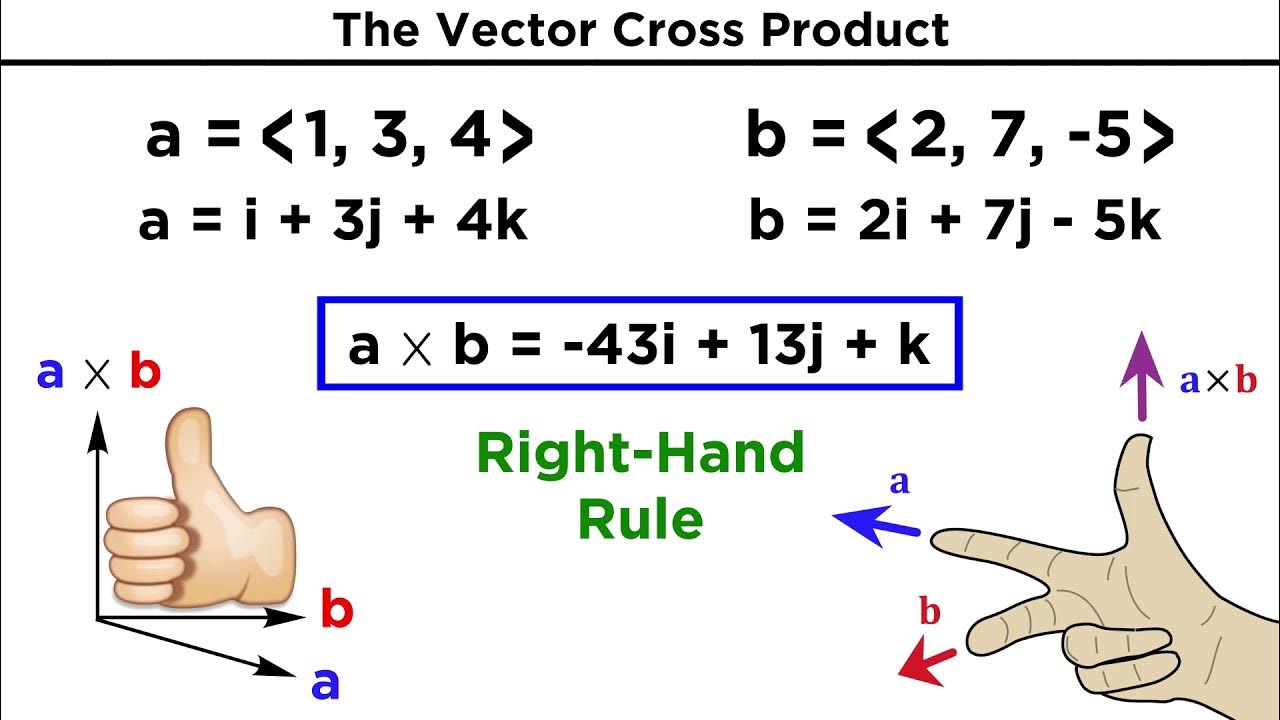
Can you provide an example of how to calculate the cross product using a determinant?
-Yes, given vectors u = (2, -1, 1) and v = (0, 2, 1), the cross product u x v is calculated by setting up a 3x3 matrix with i, j, k in the first row, components of u in the second row, and components of v in the third row. The determinant of this matrix gives the components of the cross product vector.
How does the order of the vectors affect the cross product?
-The order of the vectors in the cross product affects the direction of the resulting vector. The cross product u x v is equal to -(v x u), meaning the cross product is anti-commutative and the direction of the resulting vector is reversed when the order of the vectors is switched.
Outlines
📚 Introduction to Parallel and Orthogonal Vectors
This paragraph introduces the concept of parallel and orthogonal vectors in relation to a given vector 'w'. It explains that there are two parallel directions to any vector: one in the exact same direction as the vector (positive multiples of the vector) and one in the exact opposite direction (negative multiples of the vector). The concept of orthogonality is also introduced, stating that there are infinitely many orthogonal directions to any given vector, all lying in a plane perpendicular to the vector. The dot product is mentioned as a tool to determine orthogonality, as it equals zero when two vectors are perpendicular.
🔍 Exploring the Cross Product and Orthogonal Vectors
The second paragraph delves into the specifics of finding vectors that are orthogonal to a given vector 'w'. It discusses the use of the cross product to find a vector orthogonal to two other vectors, 'u' and 'v'. The cross product is illustrated as a method to generate a third vector from the components of 'u' and 'v', which lies in a plane perpendicular to both original vectors. The paragraph also explains the geometric interpretation of the cross product using the right-hand rule and how it can be calculated using the determinant of a matrix formed by the unit vectors and the components of 'u' and 'v'.
📘 Understanding the Determinant and Cross Product Formula
This paragraph focuses on the mathematical process of calculating the cross product using the determinant of a matrix. It provides a step-by-step guide on how to expand the determinant along the first row, multiplying each unit vector by the determinant of the 2x2 matrix formed by crossing out the corresponding row and column. The paragraph also explains the concept of Laplace expansion and how it simplifies the calculation of the cross product, avoiding the need to memorize complex formulas.
📌 Practical Examples of Cross Product Calculations
The final paragraph provides practical examples of calculating the cross product for given vectors 'u' and 'v'. It demonstrates the process of setting up a determinant matrix with unit vectors and vector components, and then performing the expansion to find the cross product. The examples show how to find 'u cross v' and 'v cross u', highlighting that these vectors point in opposite directions but are of the same length, and both are perpendicular to the plane containing 'u' and 'v'. The paragraph concludes with a mention of upcoming videos that will cover applications of cross products.
Mindmap
Keywords
💡Vector
💡Parallel Directions
💡Orthogonal Directions
💡Dot Product
💡Cross Product
💡Right-Hand Rule
💡Determinant
💡Perpendicular
💡Scalar
💡Laplace Expansion
Highlights
Introduction to the concept of parallel directions in relation to a given vector w.
Explaining that there are two parallel directions to any vector: the same and the opposite direction.
Illustration of positive multiples of a vector to represent parallel directions.
Discussion on negative multiples of a vector as another set of parallel directions.
Introduction to orthogonal directions being infinitely many compared to parallel directions.
Clarification that orthogonal vectors lie in a plane perpendicular to the original vector.
Explanation of the dot product and its relation to orthogonality.
Demonstration of finding a vector orthogonal to two given vectors using the dot product.
Introduction to the cross product and its geometric interpretation.
Description of the cross product as a method to find a vector orthogonal to two given vectors.
Explanation of the right-hand rule in the context of cross products.
Illustration of how the order of vectors in a cross product affects the resulting vector's direction.
Introduction to the determinant as a method to calculate the cross product.
Explanation of the Laplace expansion as a technique for calculating determinants.
Demonstration of calculating the cross product using determinants with examples.
Conclusion on the significance of cross products in vector mathematics and预告of upcoming applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: