The dot product | Magnetic forces, magnetic fields, and Faraday's law | Physics | Khan Academy
TLDRThe video script provides an insightful explanation of the dot product of vectors, emphasizing its simplicity and utility in physics. It defines the dot product as the product of the magnitudes of two vectors and the cosine of the angle between them. The script employs visual analogies, such as shadows and projections, to clarify the concept. It also illustrates the application of the dot product in calculating work, where the force and displacement vectors are considered. The distinction between dot product and cross product is highlighted, noting that the former results in a scalar quantity, indicative of how much the vectors reinforce each other, whereas the latter involves orthogonal components and requires consideration of orientation.
Takeaways
- 📌 The dot product is a method of multiplying vectors, considered easier than the cross product.
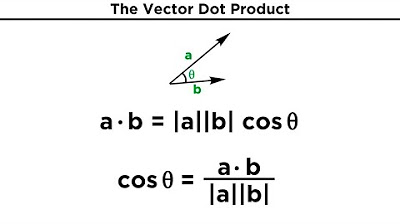
- 📐 The dot product of two vectors a and b is defined as |a|*|b|*cos(θ), where |a| and |b| are the magnitudes of vectors a and b, and θ is the angle between them.
- 🔍 Intuitive understanding of the dot product can be achieved by visualizing it as the product of the magnitude of one vector and the projection of the other vector onto it.
- 🌟 The cosine of the angle between two vectors can be interpreted as the ratio of the adjacent side to the hypotenuse in a right-angled triangle formed by one of the vectors and its projection onto the other.
- 🔄 The order of the vectors in a dot product does not matter, i.e., a·b = b·a.
- 📈 The dot product can be represented geometrically as the product of the magnitude of the projection of one vector onto the other and the magnitude of the second vector.
- 🔩 The dot product is useful in physics, for example, in calculating work, which is the product of force and displacement in the direction of the force.
- 🎯 In calculating work, only the component of the force that is in the direction of the displacement contributes to the work done.
- 🌐 The dot product results in a scalar quantity, indicating how much the vectors reinforce each other in the direction they have in common.
- 🛠️ The dot product is distinct from the cross product, which involves the orthogonal (perpendicular) components of the vectors and is sensitive to the order of the vectors and the orientation of the resulting vector.
- 📚 Understanding the dot product requires a grasp of basic trigonometry and vector concepts, and its application in various fields, such as physics, highlights its importance in vector analysis.
Q & A
What is the dot product of two vectors?
-The dot product of two vectors is a scalar quantity that is calculated as the product of the magnitudes of the two vectors and the cosine of the angle between them.
How is the dot product visually represented?
-Visually, the dot product can be represented by imagining a light source shining perpendicularly onto one of the vectors, casting a 'shadow' or projection of the other vector onto the first one.
What is the significance of the cosine of the angle in the dot product?
-The cosine of the angle in the dot product signifies the component of one vector that lies along the direction of the other vector. It measures how much of the two vectors' magnitudes are aligned in the same direction.
How does the dot product relate to the concept of work in physics?
-In physics, work is calculated as the force applied to an object times the distance moved by the object in the direction of the force. The dot product is used here to find the component of the force that is in the same direction as the displacement.
What is the result of the dot product in terms of the components of the vectors?
-The result of the dot product is a scalar that represents the product of the magnitudes of the vectors and the cosine of the angle between them, effectively measuring the extent to which the vectors' components reinforce each other.
How does the dot product differ from the cross product?
-Unlike the dot product, which results in a scalar, the cross product results in a vector. The cross product involves the orthogonal components of the vectors, and the orientation of the resulting vector depends on the order of the vectors and the right-hand rule.
Why does the order of vectors not matter in the dot product?
-The order of the vectors does not matter in the dot product because it is commutative, meaning that the dot product of two vectors a and b is the same whether you calculate a dot b or b dot a.
What is the formula for calculating the dot product of two vectors?
-The dot product of two vectors a and b, represented as a · b, is calculated using the formula: |a| * |b| * cos(θ), where |a| and |b| are the magnitudes of vectors a and b, and θ is the angle between them.
How does the dot product relate to the projection of one vector onto another?
-The dot product can be interpreted as the product of the magnitude of one vector and the projection of the other vector onto the first vector in the direction perpendicular to the second vector.
What is the physical interpretation of the dot product in the context of force and displacement?
-In the context of force and displacement, the dot product gives the component of the force that does work along the direction of the displacement. This is the part of the force that contributes to moving the object in the intended direction.
Can you provide an example calculation of the dot product?
-Sure, if we have two vectors a = (3, 4) and b = (5, -3), the dot product is calculated as follows: a · b = (3 * 5) + (4 * -3) = 15 - 12 = 3.
Outlines
📚 Introduction to the Dot Product
This paragraph introduces the concept of the dot product, a method of multiplying vectors. It explains that the dot product of two vectors is equal to the product of their magnitudes and the cosine of the angle between them. The explanation is accompanied by a visual representation of two vectors and the angle between them. The concept is further clarified by discussing the geometric interpretation of the dot product as the projection of one vector onto another, likened to a shadow cast by a light source perpendicular to one of the vectors.
💡 Application in Physics: Work Calculation
This paragraph delves into the application of the dot product in physics, specifically in calculating work. Work is defined as the force applied to an object times the distance moved by the object in the direction of the force. The paragraph uses an example of a 10 Newton object on ice, subjected to a 100 Newton force at a 60-degree angle to the horizontal direction, moved 10 meters. The calculation of work is demonstrated by finding the horizontal component of the force vector and applying it to the dot product formula, resulting in a work value measured in joules. The paragraph emphasizes the practical utility of the dot product in determining the component of force that contributes to work.
🔄 Comparison with Cross Product
The final paragraph discusses the difference between the dot product and the cross product of vectors. It highlights that the dot product results in a scalar quantity, which represents the extent to which two vectors reinforce each other in the direction they have in common. In contrast, the cross product involves the orthogonal components of the vectors, leading to a vector result that is perpendicular to both original vectors. The orientation of the cross product is noted to be important, requiring the use of the right-hand rule to determine the direction of the resulting vector. The paragraph concludes with a mention of a forthcoming video that will further explore and compare the dot and cross products.
Mindmap
Keywords
💡Dot Product
💡Vector
💡Magnitude
💡Angle
💡Cosine
💡Projection
💡Work
💡Force
💡Distance
💡Right Angle
💡Cross Product
Highlights
The dot product is considered easier to understand compared to other vector multiplication methods.
The definition of the dot product is the product of the magnitudes of two vectors and the cosine of the angle between them.
The concept of the dot product can be visually explained to enhance understanding.
The dot product can be viewed as the product of the magnitude of one vector and the cosine of the angle times the other vector.
Cosine of the angle between two vectors can be interpreted as the ratio of the adjacent side to the hypotenuse in a right-angled triangle formed by one of the vectors and its projection onto the other.
The projection of one vector onto another can be visualized as the shadow or the component of the first vector that aligns with the direction of the second.
The dot product can be used to calculate work done in physics, which is the product of the force vector and the distance vector in the direction of the force.
The work done can be calculated using the dot product of the force and distance vectors, considering only the component of the force in the direction of the movement.
The dot product results in a scalar quantity, which represents the extent to which two vectors reinforce each other in the direction of one another.
The order of the vectors in a dot product does not matter, unlike the cross product where the orientation and direction are important.
The dot product is a way to determine how much of one vector's magnitude aligns with the direction of another vector.
The dot product can be thought of as a measure of the similarity between two vectors in terms of their directional alignment.
The dot product is a fundamental concept in vector mathematics with applications in various fields such as physics and engineering.
Understanding the dot product is crucial for grasping other vector operations such as the cross product and their respective applications.
The dot product can be used to calculate the magnitude of the projection of one vector onto another, which is a key concept in vector analysis.
The dot product is a scalar and can be used to find the work done by a force on an object when the force and displacement are not aligned.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: