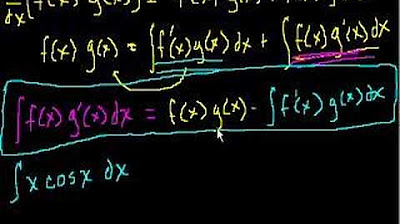Integration by parts intro | AP Calculus BC | Khan Academy

Khan Academy
28 Jan 201303:52
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the concept of integration by parts, which is derived from the product rule. It explains how to take the derivative of a product of two functions and then find its antiderivative. The process involves applying the product rule in reverse, integrating the derivative of one function times the other function, and then solving for the desired integral. This method is showcased as a powerful tool for simplifying complex integrals, which will be further demonstrated in the subsequent video.

Takeaways
  • 📚 The video begins with a review of the product rule, a fundamental concept in calculus.
  • 🔄 The product rule is key to understanding the derivation of the integration by parts formula.
  • 🅿️ The integration by parts formula can be considered the inverse of the product rule.
  • 🌟 The script demonstrates how to express a function as a product of two other functions, f(x)g(x).
  • 📈 The derivative of the product f(x)g(x) is detailed, following the product rule formula.
  • 🔄 The process of taking the antiderivative of both sides of the equation is explained.
  • 🎯 The goal is to solve for the integral of the product of two functions, leading to the integration by parts formula.
  • ➖ The solution involves subtracting the antiderivative of the first function times the derivative of the second from the product of the functions.
  • 📝 The final form of the integration by parts formula is presented in a traditional textbook format.
  • 🤔 The script acknowledges the potential initial skepticism about the utility of the integration by parts formula.
  • 🚀 The next video will show how the integration by parts formula can simplify complex integrals.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the review of the product rule and the derivation of the integration by parts formula.

  • How is the product rule expressed in the context of the video?

    -The product rule is expressed as the derivative of a product of two functions, f(x) and g(x), which is (f'(x) * g(x)) + (f(x) * g'(x)).

  • What is the inverse operation of the product rule?

    -The inverse operation of the product rule is the integration by parts, which helps in finding the antiderivative of a product of two functions.

  • How does the video demonstrate the transition from the product rule to integration by parts?

    -The video demonstrates this by taking the antiderivative of both sides of the product rule equation, leading to the integration by parts formula.

  • What is the general form of the integration by parts formula?

    -The general form of the integration by parts formula is ∫f(x)g'(x)dx = f(x)g(x) - ∫f'(x)g(x)dx.

  • Why might the integration by parts formula be useful in calculus?

    -The integration by parts formula is useful because it can simplify the process of finding antiderivatives for products of functions, especially in complex integrals.

  • How does the video suggest the utility of the integration by parts formula?

    -The video suggests that the integration by parts formula can simplify the process of taking antiderivatives and make it easier to handle complex integrals, as demonstrated in the next video.

  • What is the significance of reviewing the product rule in understanding integration by parts?

    -Reviewing the product rule is significant because it provides the foundation for understanding how the integration by parts formula works, as it is derived from the product rule.

  • What is the role of the antiderivative in deriving the integration by parts formula?

    -The antiderivative plays a crucial role in deriving the integration by parts formula, as it is applied to both sides of the product rule equation to lead to the new formula.

  • How does the video emphasize the importance of the integration by parts formula?

    -The video emphasizes the importance of the integration by parts formula by showing that it can be a powerful tool for simplifying complex integrals and making calculus problems more manageable.

  • What is the step-by-step process shown in the video for deriving the integration by parts formula?

    -The step-by-step process includes: (1) applying the product rule to a function expressed as a product of two other functions, (2) taking the antiderivative of both sides of the resulting equation, (3) solving for the specific part of the equation that involves the product of the first function and the derivative of the second, and (4) rearranging the formula to match the traditional textbook form.

Outlines
00:00
📚 Introduction to Integration by Parts

This paragraph introduces the concept of integration by parts, which is derived from the product rule. It explains that if a function f(x) can be expressed as a product of two other functions, then the derivative of this product can be found using the product rule. The paragraph then proceeds to illustrate how to take the antiderivative of both sides of the resulting equation, leading to the formula for integration by parts. The explanation emphasizes the utility of this method in simplifying complex integrals, even though it may still involve an integral within the process.

Mindmap
Keywords
💡Integration by Parts
Integration by Parts is a method used in calculus to evaluate integrals, particularly when the integral is a product of two functions. It is based on the product rule for differentiation and can be considered as its inverse. In the video, the process of deriving this formula is explained by taking the derivative of a product of two functions and then integrating both sides of the equation. The formula is used to simplify complex integrals by breaking them down into more manageable parts, as demonstrated by the example of integrating the product of f(x) and g'(x). This technique is crucial for solving problems in calculus that involve products of functions.
💡Product Rule
The Product Rule is a fundamental rule in calculus that describes how to differentiate a product of two or more functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the context of the video, the Product Rule is reviewed as a precursor to understanding Integration by Parts, as the latter is essentially the reverse process of the former.
💡Derivative
A derivative in calculus represents the rate of change or the slope of a function at a particular point. It is a fundamental concept used to analyze the behavior of functions, such as their increases, decreases, and turning points. In the video, derivatives are calculated as part of the process to derive the Integration by Parts formula, where the derivative of a product of functions is considered.
💡Antiderivative
An antiderivative, also known as an indefinite integral, is a function whose derivative is the given function. It is the inverse operation of differentiation and is used to find the original function from its derivative. In the video, the concept of the antiderivative is utilized to derive the Integration by Parts formula, where the goal is to find the antiderivative of a product of two functions.
💡f(x) and g(x)
f(x) and g(x) are placeholders for functions in the context of the video. They represent the two functions whose product is being integrated or differentiated, according to the Product Rule and Integration by Parts. These functions can be any valid mathematical expressions depending on the specific problem being solved.
💡f'(x) and g'(x)
f'(x) and g'(x) represent the derivatives of the functions f(x) and g(x), respectively. They are used in the application of the Product Rule for differentiation and the Integration by Parts formula. The derivatives describe the rate of change or the slopes of the original functions at any given point.
💡Constant
In the context of the video, the constant refers to the constant of integration, which is an arbitrary constant that is added when finding the antiderivative of a function. This constant accounts for the fact that the derivative of a constant is zero, and thus, the antiderivative can shift up or down without changing the derivative.
💡Review
The term 'review' in the context of the video refers to the process of revisiting and reinforcing previously learned concepts or rules. The video begins with a review of the Product Rule, which is essential for understanding the subsequent discussion on Integration by Parts. This review helps to ensure that the viewer has a solid foundation of the necessary mathematical principles before moving on to more complex material.
💡Simplify
To simplify in mathematics means to make a complex expression or equation more straightforward or easier to understand or work with. In the context of the video, simplifying refers to the process of using Integration by Parts to transform a complicated integral into a more manageable form. This often involves breaking down the integral into smaller parts that can be more easily evaluated.
💡Inverse
An inverse in mathematics is an operation that reverses the effect of another operation. In the context of the video, the Integration by Parts formula is described as the inverse of the Product Rule because it undoes the process of differentiation described by the Product Rule. The video shows how this inverse relationship allows for the evaluation of integrals that are products of two functions.
💡Complex Integrals
Complex integrals refer to integrals that are difficult to evaluate directly due to the nature of the functions involved. These could be products of functions, integrals with variable limits, or other forms that do not have straightforward antiderivatives. The video discusses how Integration by Parts can be used to simplify complex integrals by transforming them into a sum of simpler integrals.
Highlights

Reviewing the product rule, a fundamental concept in calculus.

Deriving the integration by parts formula, an essential technique for solving complex integrals.

Expressing a function as a product of two other functions, f(x) = f(x) * g(x), to apply the product rule.

Applying the derivative operator to a product of functions, resulting in a sum of two terms.

Taking the antiderivative of both sides of the product rule equation to transition towards integration by parts.

Ignoring the constant when taking the antiderivative, as it does not affect the final result.

Solving for the integral of the product of functions, which is the core of integration by parts.

Subtracting the second term from both sides of the equation to isolate the desired integral.

Expressing the integration by parts formula in a clear and traditional textbook format.

Understanding that the integration by parts formula can be applied to integrals of the form f(x) times the derivative of another function.

Recognizing that the integration by parts technique can simplify complex integrals, even when an integral remains.

The video serves as a review of foundational calculus concepts, suitable for strengthening understanding.

The integration by parts method can be viewed as the inverse of the product rule, providing a new perspective.

The process of moving from the product rule to integration by parts demonstrates the interconnectedness of calculus concepts.

The video promises to show in the next installment how integration by parts can significantly simplify complex integrals.

Transcripts

Browse More Related Video

The Product Rule for Derivatives — Topic 57 of Machine Learning Foundations

Calculus - Integration By Parts

Integration by Parts

Taking the derivative of two binomials using product and chain rule

Indefinite Integration (part V)

BusCalc 11 Derivative Product Rule

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Calculus TechniquesIntegration by PartsProduct RuleMathematics EducationInverse OperationsDifferential EquationsAcademic LearningOnline TutorialMathematical AnalysisEducational Content