Unbiased Estimators (Why n-1 ???) : Data Science Basics
TLDRIn this enlightening video, we dive into the concept of unbiased estimators, specifically addressing the intriguing question of why the sample variance formula uses a denominator of 'n - 1' instead of 'n'. We embark on a journey through a hypothetical scenario in Statsville, where we aim to estimate the population's age variance using a smaller sample size. Through clear explanations and a step-by-step mathematical demonstration, we reveal that the 'n - 1' denominator acts as a correction factor, ensuring our estimator remains unbiased. This video offers both intuitive and mathematical insights into a fundamental statistical principle, making it accessible to learners at various levels.
Takeaways
- 📊 The video addresses the concept of unbiased estimators, specifically focusing on why the sample variance formula includes '1 over n minus 1' instead of '1 over n'.
- 🔍 Sample variance is a crucial statistical tool used to estimate the variance of a population based on a sample, and understanding its calculation is key for accurate statistical analysis.
- 🏘️ The example used involves a hypothetical town called Statsville with a population of one million, demonstrating how sample data is used to estimate population metrics like average age.
- 👥 The video clarifies the symbols 'mu' and 'sigma squared' as representing the true average age and the true variance of the town's population, which are unknown and estimated through sampling.
- 📈 The sample mean (x bar) is calculated by averaging the ages in the sample, a straightforward and commonly understood concept in statistics.
- 💡 The sample mean's calculation is shown to be unbiased, meaning its expected value equals the population mean, demonstrating a desirable property in statistics.
- 🤔 The sample variance calculation, using '1 over n minus 1', is more complex and less intuitive than the sample mean, leading to the main discussion in the video.
- 📐 The mathematical proof shows that using '1 over n minus 1' in the variance formula makes the estimator unbiased, unlike '1 over n', which would introduce bias.
- ⚖️ An intuitive explanation is given: a sample typically underestimates the true population variance, and the '1 over n minus 1' factor corrects for this by slightly increasing the estimated variance.
- 🎓 The video concludes by emphasizing the importance of understanding why certain formulas are used in statistics, not just how to use them.
Q & A
Why is the denominator in the sample variance formula \(1/(n-1)\) instead of \(1/n\)?
-The \(1/(n-1)\) in the sample variance formula acts as a correction factor to account for the bias in estimating the population variance from a sample. Since a sample likely misses out on some of the population's variation, using \(n-1\) instead of \(n\) compensates for this underestimation, making the sample variance an unbiased estimator of the population variance.
What is meant by 'bias of an estimator' in statistics?
-The bias of an estimator refers to the difference between the expected value of the estimator and the true value of the parameter it is estimating. An unbiased estimator has a bias of zero, meaning that on average, it accurately estimates the true parameter value.
How is the sample mean (\(\overline{x}\)) calculated, and why is it considered an unbiased estimator?
-The sample mean (\(\overline{x}\)) is calculated by summing all individual data points in the sample and dividing by the number of points (\(n\)). It is considered an unbiased estimator because its expected value equals the population mean (\(\mu\)), indicating that on average, it correctly estimates the true average of the population.
Can you explain the role of \(n-1\) in reducing the bias of the sample variance?
-The role of \(n-1\) is to adjust the scale of the sample variance so it more accurately reflects the population variance. By using \(n-1\) instead of \(n\), the calculation compensates for the reduced variability in a sample compared to the entire population, thus reducing the estimator's bias.
Why does the bias in a sample variance estimator decrease as the sample size \(n\) increases?
-As the sample size \(n\) increases, the factor \((n-1)/n\) in the biased version of the sample variance formula approaches 1, making the bias smaller. This means the larger the sample size, the closer the biased estimator's expected value is to the population variance, reducing the effect of bias.
What is the impact of using a sample to estimate population parameters in terms of bias?
-Using a sample to estimate population parameters can introduce bias if not corrected for. This bias occurs because samples may not perfectly represent the population's variability. Correcting for bias, such as using \(n-1\) in the variance calculation, helps make estimators more accurate.
How does the concept of bias relate to the practical process of sampling in statistics?
-In practical sampling, bias relates to how well the sample reflects the population. Estimators like the sample mean and variance aim to infer population parameters accurately. Adjustments for bias, like using \(n-1\) for variance, ensure these estimations are unbiased on average, despite the sample's limitations.
What practical example is used in the script to illustrate the concept of estimating population parameters?
-The script uses the example of a census bureau in a town called Statsville, with 1 million residents, to illustrate estimating population parameters. It discusses how to estimate the average age and variance of age in the population using a smaller, randomized sample.
How does the concept of bias adjustment in the sample variance formula support statistical analysis?
-Bias adjustment in the sample variance formula supports statistical analysis by ensuring that estimates of population variance are unbiased and accurate. This adjustment recognizes the limitations of samples and corrects for potential underestimation of variability, improving the reliability of statistical conclusions.
What intuition is provided to explain why \(n-1\) is used in the denominator for sample variance?
-The intuition is that taking a sample inevitably misses some of the population's variation, especially the extremes. By using \(n-1\) in the denominator, it acknowledges this missing variation and adjusts the variance estimate upwards, assuming the population variance to be slightly higher than the sample suggests.
Outlines
📊 Introduction to Unbiased Estimators and Sample Variance
The paragraph introduces the concept of unbiased estimators in statistics, specifically focusing on the question of why the sample variance formula includes a (n-1) in the denominator instead of n. The speaker explains that while this might seem confusing at first, there is a mathematical and intuitive reason behind it. The context is set with a hypothetical situation where the speaker works for the census bureau of a town called Statsville, which has a population of one million. The goal is to estimate the average age and variance of the population using a small sample due to impracticality of surveying everyone. The speaker introduces two metrics, mu (the true average age) and sigma squared (the true variance of ages), and explains that the sample mean (x bar) is calculated by summing all ages in the sample and dividing by n. The concept of bias in estimators is introduced, with the bias of the sample mean (x bar) being calculated and found to be zero, indicating that it is an unbiased estimator.
🔍 Understanding the Unbiased Estimator for Sample Variance
This paragraph delves deeper into the concept of unbiased estimators, specifically focusing on the sample standard deviation and variance. The speaker explains that while the sample variance (s squared) seems intuitively to be calculated with a denominator of n, using n-1 instead results in an unbiased estimator. The bias of the sample standard deviation is defined and calculated, revealing that using n in the denominator would result in a biased estimator. The speaker provides a visual example to help the audience understand why using n-1 compensates for the underestimation of population variance that occurs due to not capturing the entire population's variation in a sample. The explanation concludes with the speaker emphasizing the importance of using n-1 to obtain an accurate estimate of the population variance.
Mindmap
Keywords
💡Unbiased Estimators
💡Sample Variance
💡Bias of an Estimator
💡Population vs. Sample
💡Sample Mean (X̄)
💡Correction Factor
💡Degrees of Freedom
💡Expected Value
💡Population Variance (σ²)
💡Intuition Behind n-1
Highlights
Introduction to unbiased estimators and the rationale behind the sample variance formula.
Setting up a statistical scenario involving the Census Bureau of a town called Statsville.
Defining key statistical metrics: mu (true average age) and sigma squared (true variance of age).
Explaining the concept of a randomized sample and its significance in statistics.
Introduction to sample mean (x bar) as an estimator for mu.
Discussion on the intuitive approach to calculating sample variance and its issues.
Defining the bias of an estimator and its importance in statistical estimation.
Demonstrating that the sample mean (x bar) is an unbiased estimator of mu.
Introducing the bias calculation for the sample variance and its complexity.
Mathematical proof that using 1 over (n-1) in sample variance calculation results in an unbiased estimator.
Comparison between using 1 over n and 1 over (n-1) in variance calculation and the bias implications.
Illustrative explanation of why a sample may underestimate population variance.
Justification for the 1 over (n-1) correction factor in sample variance to account for underestimated variance.
Concluding remarks on the importance of understanding the 1 over (n-1) factor in sample variance calculations.
Encouragement for further exploration and understanding of statistical estimators.
Transcripts
Browse More Related Video

Variance: Why n-1? Intuitive explanation of concept and proof (Bessel‘s correction)
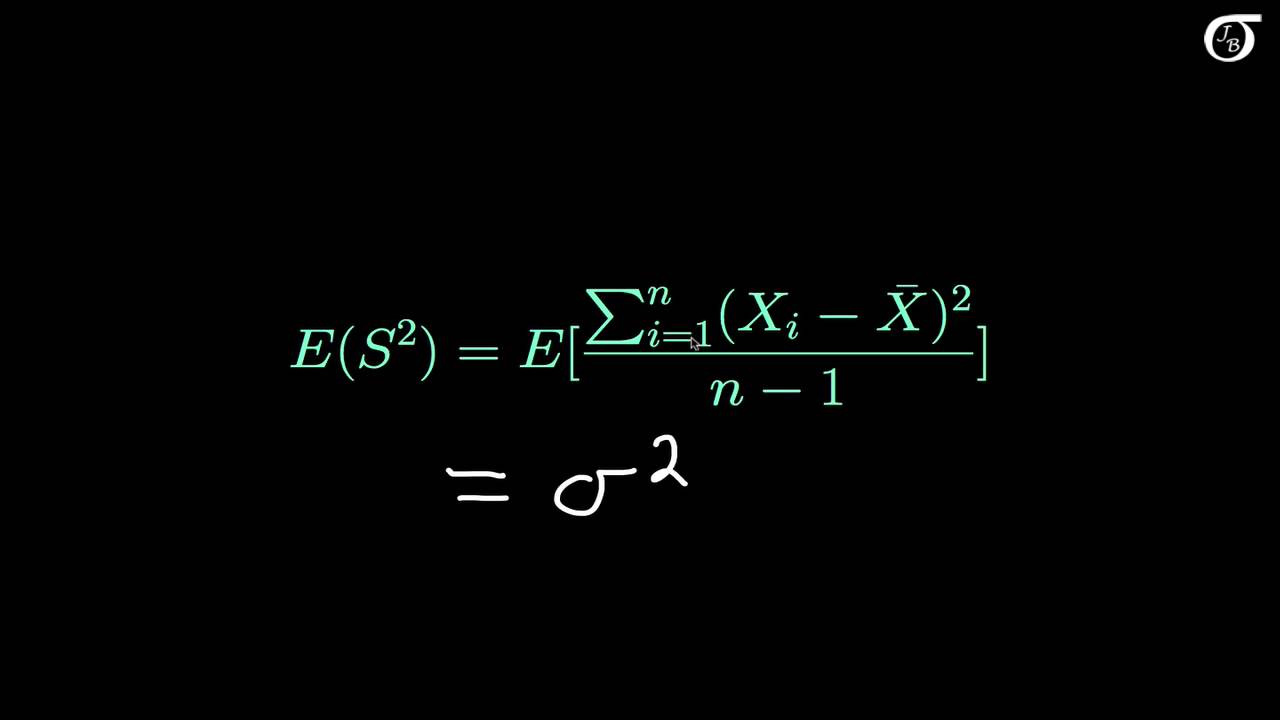
Proof that the Sample Variance is an Unbiased Estimator of the Population Variance
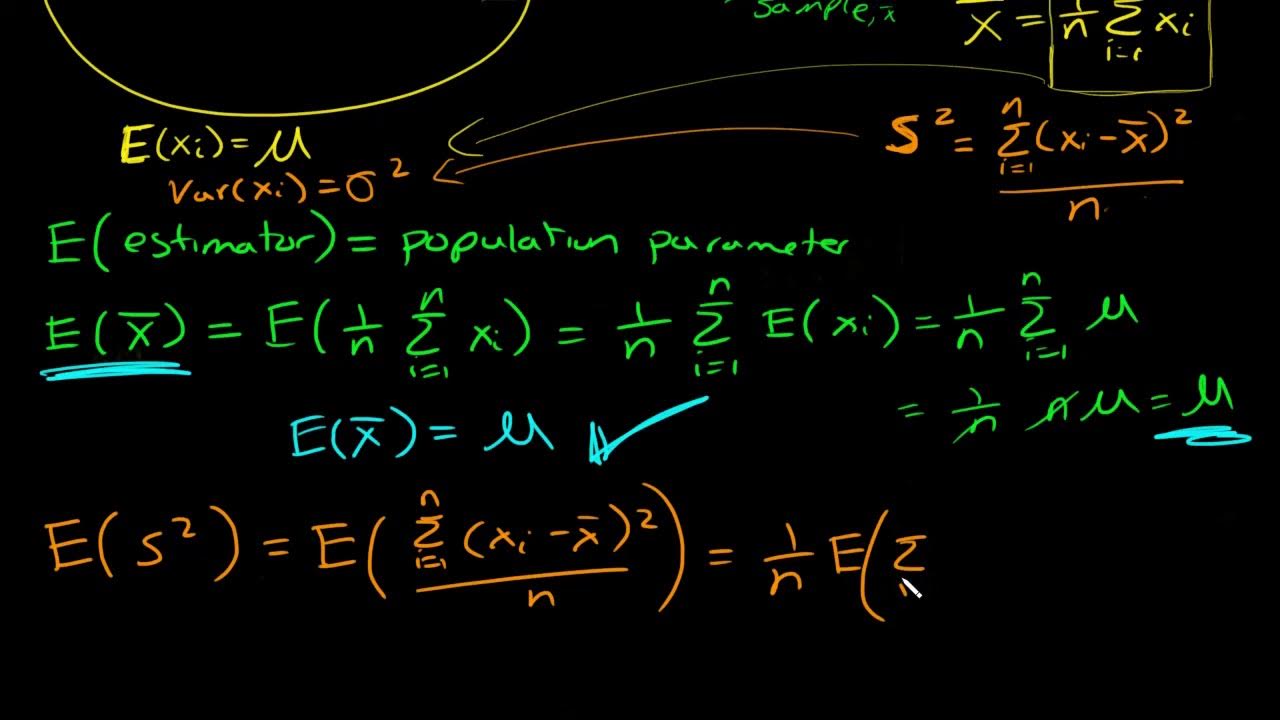
What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var
Simulation showing bias in sample variance | Probability and Statistics | Khan Academy

Review and intuition why we divide by n-1 for the unbiased sample | Khan Academy
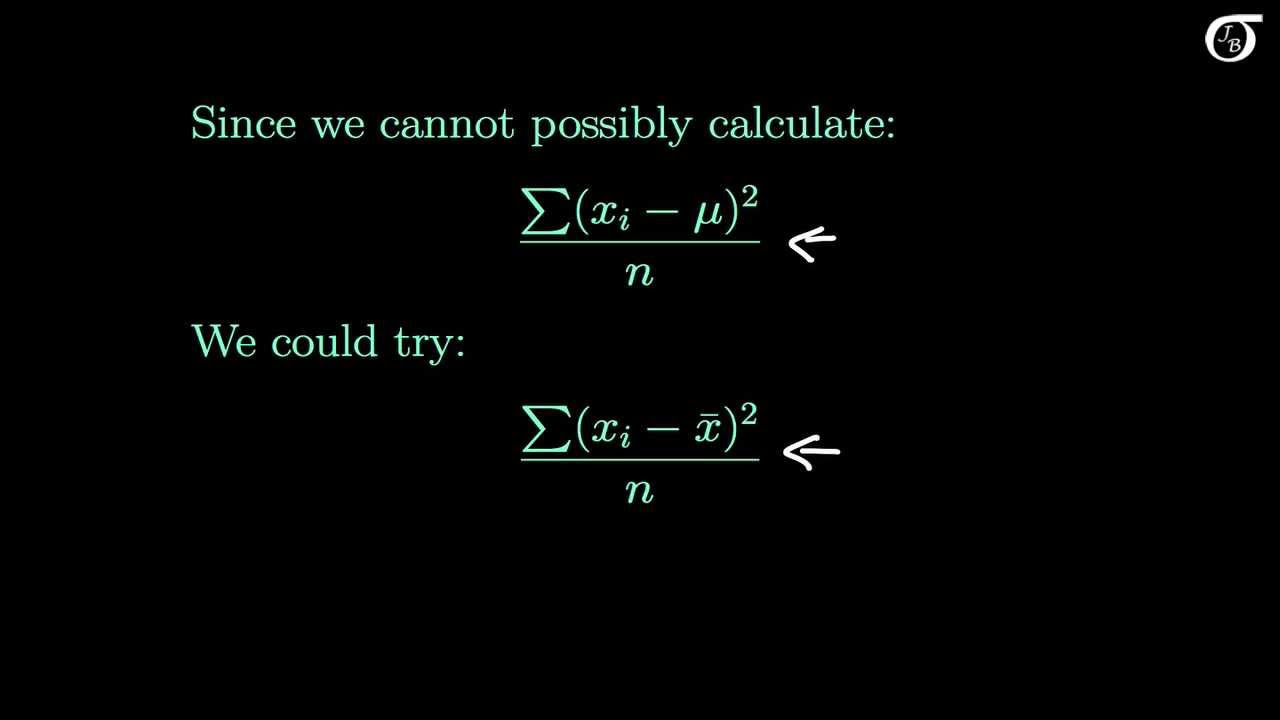
The Sample Variance: Why Divide by n-1?
5.0 / 5 (0 votes)
Thanks for rating: