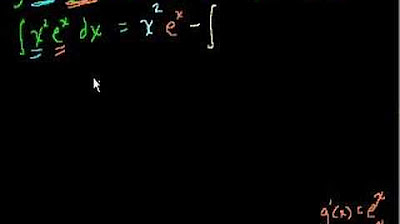Calculus - Integration By Parts
TLDRThe video script presents a detailed walkthrough on how to find the indefinite integral of a three-product term expression using integration by parts. It begins by explaining the product rule and the standard integration by parts formula for two-product term expressions, then extends the concept to the more complex scenario of three-product terms. The process is demonstrated through the integration of the specific function x sine x e^(2x), with each step clearly outlined, including the necessary derivatives and antiderivatives. The final answer is verified by differentiating it to match the original function. The explanation is methodical, ensuring a comprehensive understanding of the integration by parts technique for complex integrals.
Takeaways
- 📚 The concept of integration by parts is introduced as an extension of the product rule for derivatives.
- 🔄 Integration by parts formula for a two-term product is uv - vdu, which reverses the process of differentiation.
- 📈 The script derives a formula for integration by parts for three-term products using the product rule for derivatives.
- 🌟 The process involves differentiating each term in the product and rearranging the terms to find the integral.
- 🧩 The application of the formula is demonstrated by solving the integral of x * sin(x) * e^(2x) dx.
- 🔢 The solution involves breaking down the integral into manageable parts and applying integration by parts multiple times.
- 🔄 The method requires finding suitable u and dv for each part of the integral and simplifying the resulting expressions.
- 📊 The process is repeated until all terms are integrated, and the final answer is a combination of all the individual results.
- 🔍 Verification of the solution is done by differentiating the result to see if it matches the original integrand.
- 🎓 The video provides a step-by-step walkthrough, making it an educational resource for those learning integration techniques.
- 💡 The key takeaway is the ability to apply integration by parts to more complex expressions with multiple terms.
Q & A
What is the main topic of the video script?
-The main topic of the video script is finding the indefinite integral of a three product term expression using integration by parts.
How does the integration by parts formula work for a two product term expression?
-For a two product term expression, the integration by parts formula works by stating that the integral of u dv is equal to uv minus the integral of v du.
What is the product rule in calculus?
-The product rule in calculus is a method for finding the derivative of two functions that are multiplied together. It states that the derivative of u times v is u prime times v plus u times v prime.
How does the video script derive the integration by parts formula for a three product term expression?
-The video script derives the integration by parts formula for a three product term expression by first finding the derivative of the three terms, then replacing the derivatives with their differentials, rearranging the equation, and finally integrating both sides.
What is the integral of x sine x e to the 2x?
-The integral of x sine x e to the 2x is 2/5 x sine x e to the 2x minus 3/25 sine x e to the 2x minus 1/5 x cosine x e to the 2x plus 4/25 cosine x e to the 2x plus C, where C is the constant of integration.
How does the video script verify the correctness of the derived integral?
-The video script verifies the correctness of the derived integral by taking the derivative of the right side of the equation and ensuring it matches the original expression on the left side.
What is the significance of the constant 'C' in the final answer?
-The constant 'C' represents the constant of integration, which is added to the antiderivative to account for the infinite number of possible antiderivatives that can differ by a constant.
How does the video script handle the complexity of the integral with multiple terms?
-The video script handles the complexity by breaking down the problem into smaller parts, applying integration by parts multiple times, and carefully keeping track of the terms and their derivatives.
What is the role of the product rule in deriving the integration by parts formula?
-The product rule plays a crucial role in deriving the integration by parts formula as it helps to reverse the process of finding the derivative, which is the basis for the integration by parts method.
How does the video script demonstrate the application of the integration by parts formula?
-The video script demonstrates the application of the integration by parts formula by walking through the step-by-step process of solving a complex integral involving a three product term expression.
What are the key steps in solving the integral of x sine x e to the 2x as outlined in the video script?
-The key steps include identifying the functions u, v, and w, finding their derivatives and antiderivatives, applying the integration by parts formula, simplifying the resulting expressions, and verifying the solution by differentiation.
Outlines
📚 Introduction to Integration by Parts for Three Product Term Expressions
This paragraph introduces the concept of finding the indefinite integral of a three product term expression using integration by parts. It explains that while integration by parts is typically used for two product term expressions, the process can be extended to more complex expressions. The paragraph outlines the need to understand the derivation of the integration by parts formula from the product rule of finding derivatives, which is essential for applying it to more complicated integrals.
🧠 Deriving the Integration by Parts Formula for Three Product Terms
The paragraph delves into the process of deriving the integration by parts formula for a three product term expression. It begins by discussing the product rule for derivatives and how integration by parts is essentially the reverse process. The explanation includes the step-by-step derivation of the formula by differentiating each part of the expression and rearranging the terms to find the integral. The paragraph aims to provide a clear understanding of the mathematical process behind integration by parts for complex expressions.
🔍 Application of Integration by Parts to a Specific Problem
This paragraph demonstrates the application of the integration by parts formula to a specific problem involving a three product term expression: the integral of x sine x e^(2x) dx. The paragraph breaks down the process of identifying the u, v, and w components of the expression and calculating their derivatives. It then illustrates how to apply the formula to find the integral, emphasizing the importance of carefully handling each term and integrating each part.
📝 Simplifying the Integral of a Complex Expression
The paragraph focuses on simplifying the integral of the complex expression x sine x e^(2x) by applying integration by parts multiple times. It explains how to simplify the resulting integrals and combine like terms to obtain a more manageable expression. The paragraph also highlights the need to distribute constants and deal with negative signs, ultimately leading to a simpler form of the integral.
🔧 Further Simplification and Combining Terms
This paragraph continues the process of simplifying the integral by further applying integration by parts to the remaining complex terms. It explains how to simplify the expressions by combining like terms and using the properties of sine and cosine functions. The paragraph emphasizes the importance of carefully tracking the signs and coefficients of each term to ensure the correct simplification of the integral.
🏁 Verification of the Derived Integral
The final paragraph is dedicated to verifying the correctness of the derived integral. It explains the process of taking the derivative of the final answer and comparing it to the original expression to ensure that the integration by parts was applied correctly. The paragraph concludes with a confirmation that the derived integral is indeed correct, providing a sense of closure to the explanation of the integration by parts for three product term expressions.
Mindmap
Keywords
💡Integration by Parts
💡Product Rule
💡Derivative
💡Indefinite Integral
💡Three Product Term Expression
💡Antiderivitive
💡e to the 2x
💡x sine x
💡Cosine Function
💡Differential dx
Highlights
Integration by parts is a method for finding the indefinite integral of a function.
Integration by parts is the reverse process of finding the derivative using the product rule.
The formula for integration by parts is ∫(uv)'dx = uv - ∫v(u')dx, where u and v are functions of x.
To apply integration by parts to a three product term expression, differentiate each part and rearrange terms accordingly.
The derivative of a three product term expression is found by differentiating each term individually and applying the product rule.
When rearranging terms, multiply each term by dx and then move terms across the equation to isolate the derivatives.
After rearranging, the integration by parts formula for a three product term expression is derived.
To solve the integral of x*sin(x)*e^(2x) dx, identify u, v, and w according to the expression.
When applying the formula, the integral becomes a combination of simpler integrals that can be solved individually.
Some integrals may require applying integration by parts multiple times due to the complexity of the expression.
When solving multi-step integrals, it's important to keep track of the constants and distribute them appropriately.
Combining like terms and simplifying expressions is crucial for obtaining the final answer.
Verification of the solution can be done by taking the derivative of the answer and comparing it to the original integrand.
The process of integration by parts, especially for complex expressions, involves breaking down the expression into manageable parts.
Integration by parts is a powerful tool for solving integrals of products of functions, including those that do not appear to fit the standard formula structure.
The example provided demonstrates the process of solving the integral of x*sin(x)*e^(2x) dx using integration by parts.
The final answer for the integral of x*sin(x)*e^(2x) dx is 2/5 * x*sin(x)*e^(2x) - 3/25 * sin(x)*e^(2x) - 1/5 * x*cos(x)*e^(2x) + 4/25 * cos(x)*e^(2x) + C.
The example serves as a guide for tackling more complex integrals using integration by parts and illustrates the importance of methodical problem-solving.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: