Review and intuition why we divide by n-1 for the unbiased sample | Khan Academy

Khan Academy
21 Nov 201209:44
EducationalLearning
32 Likes 10 Comments

TLDRThe video script delves into the concept of estimating population variance using sample data. It explains the difference between a biased and an unbiased estimate of variance, highlighting the importance of using 'n minus 1' in calculations for the latter. The script provides a visual intuition for why dividing by a smaller number (n-1) in the sample variance formula can give a more accurate reflection of the true population variance, emphasizing that the unbiased estimate accounts for the sample mean's position within the data set.

Takeaways
  • πŸ“Š Understanding the difference between a population and a sample is fundamental, with the population (capital N) being the entire dataset and the sample (lowercase n) being a subset of it.
  • 🎯 The mean of a population is a parameter denoted by the Greek letter mu (ΞΌ), calculated by summing all data points and dividing by the total number of points (N).
  • πŸ“ˆ The sample mean, denoted by x-bar, is calculated similarly to the population mean but using the data points from the sample (n) and dividing by the sample size.
  • πŸ”’ Variance for a population is denoted by the Greek letter sigma squared (σ²) and is the mean of the squared distances from the population mean.
  • πŸ”„ Sample variance can be calculated in two ways: the biased estimator (dividing by n) and the unbiased estimator (dividing by n-1).
  • 🧠 The biased sample variance might underestimate the true population variance because the sample mean is always within the data and might not accurately represent the population mean.
  • πŸ“‰ Dividing by n-1 instead of n in the calculation of sample variance gives an unbiased estimate, which tends to be a better approximation of the population variance.
  • πŸ€” The intuition behind dividing by n-1 is that it accounts for the fact that the sample mean is part of the sample and not an external value.
  • 🌟 The unbiased estimate is generally preferred when trying to infer properties of the population from a sample because it doesn't assume the sample mean is known.
  • πŸ’‘ The video script suggests that in the future, a computer program could be used to further demonstrate why dividing by n-1 provides a better estimate of the population variance.
  • πŸ“ It's important to clarify when discussing sample variance whether one is referring to the biased or unbiased estimate, as the context can significantly impact the interpretation of the results.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is understanding why we divide by n minus 1 when calculating an unbiased estimate of the population variance from a sample.

  • What is the difference between a parameter and a statistic?

    -A parameter is a characteristic or measure of a population, while a statistic is a characteristic or measure of a sample. For example, the population mean is a parameter, and the sample mean is a statistic.

  • How is the population mean calculated?

    -The population mean is calculated by summing all data points in the population and then dividing by the total number of data points (N).

  • How is the sample mean denoted and calculated?

    -The sample mean is denoted with the letter 'x' and a bar over it. It is calculated by summing all data points in the sample and then dividing by the number of data points in the sample (n).

  • What is variance and how is it calculated for a population?

    -Variance is a measure of how much the data points in a set vary from the mean. For a population, variance is calculated by taking each data point, subtracting the population mean, squaring the result, and then dividing by the total number of data points.

  • What are the two types of sample variance discussed in the video?

    -The two types of sample variance discussed are the biased sample variance and the unbiased estimator of the population variance.

  • How is the biased sample variance calculated?

    -The biased sample variance is calculated by taking each data point in the sample, subtracting the sample mean, squaring the result, and then dividing by the number of data points in the sample (n).

  • Why might the biased sample variance underestimate the true population variance?

    -The biased sample variance might underestimate the true population variance because the sample mean will always be within the range of the sample data points, potentially leading to smaller squared distances from the mean when compared to the actual distances from the true population mean.

  • How is the unbiased estimate of the population variance calculated?

    -The unbiased estimate of the population variance is calculated by taking each data point in the sample, subtracting the sample mean, squaring the result, and then dividing by the number of data points in the sample minus 1 (n-1).

  • What is the main intuition behind dividing by n minus 1 in the calculation of the unbiased sample variance?

    -Dividing by n minus 1 gives a larger value and helps to correct for the underestimation that can occur when the sample mean is used in place of the population mean, as the sample mean is always within the sample and may not fully represent the dispersion of the entire population.

  • What does the video suggest about the relationship between the sample mean and the population mean?

    -The video suggests that the sample mean is likely to be within the range of the sample data points and may not accurately represent the true population mean, especially when the sample size is small.

  • What is the potential benefit of using an unbiased estimate of the population variance?

    -Using an unbiased estimate of the population variance provides a more accurate representation of the true dispersion of the data points in the population, which is essential for statistical analysis and making inferences about the population based on sample data.

Outlines
00:00
πŸ“Š Understanding Population and Sample Statistics

This paragraph introduces the concepts of population and sample statistics, focusing on the mean and variance. It explains that the population mean is a parameter calculated by summing all data points in the population and dividing by the number of data points (N). Similarly, the sample mean is a statistic calculated from a subset of the population (n). The paragraph also discusses the population variance, which is the mean of squared distances from the population mean, and contrasts it with the sample variance, highlighting the difference between the biased and unbiased estimates of the population variance.

05:00
πŸ” Bias in Sample Variance and the Role of n Minus 1

This paragraph delves into the concept of bias in the calculation of sample variance. It explains why dividing by n (the number of data points in the sample) instead of n-1 can lead to a biased underestimate of the population variance. The key idea is that the sample mean is always within the range of the sample data points, which can lead to a smaller estimate of the variance compared to the true population variance. By dividing by n-1, the calculation provides an unbiased estimate that is more representative of the population variance, even though it results in a larger value.

Mindmap
Keywords
πŸ’‘Unbiased estimate
An unbiased estimate is a statistical measure that does not systematically overestimate or underestimate the true value of a parameter. In the context of this video, the unbiased estimate refers to a method of calculating the sample variance in a way that does not favor any particular result, providing a more accurate reflection of the population variance. The video explains that dividing by 'n-1' instead of 'n' in the variance formula gives an unbiased estimate, as it corrects for the bias introduced by using the sample mean in the calculation.
πŸ’‘Population variance
Population variance is a statistical measure that quantifies the spread or dispersion of a set of data points in an entire population. It is calculated as the average of the squared differences between each data point and the population mean. In the video, the population variance is a key concept as the goal is to estimate it using sample data. The video discusses the importance of accurately estimating the population variance and the impact of sampling on this estimation.
πŸ’‘Sample variance
Sample variance is an estimate of the population variance based on a sample of data. It is calculated using the same formula as population variance but applied to the sample data instead of the entire population. The video emphasizes the difference between a biased and an unbiased estimate of sample variance, highlighting the importance of using the correct method to obtain a reliable approximation of the population variance.
πŸ’‘Sample mean
The sample mean, denoted by the Greek letter mu, is the average of all data points in a sample. It is used as an estimate for the population mean and is calculated by summing all the data points in the sample and then dividing by the number of data points. In the video, the sample mean is crucial for understanding how the sample variance is calculated and how it relates to the population variance.
πŸ’‘Population mean
The population mean is the average of all data points in an entire population. It serves as a benchmark or true value around which individual data points are distributed. In statistical analysis, the population mean is often of interest, and it is estimated through sample data when the entire population is too large to measure directly. The video script discusses the concept of the population mean in the context of calculating both the population variance and the sample variance.
πŸ’‘Bias
In statistics, bias refers to the tendency of a statistical estimator to consistently produce an outcome that deviates from the true value. The video script specifically discusses how the biased sample variance can underestimate the population variance because it uses the sample mean in its calculation, which is inherently tied to the specific sample chosen.
πŸ’‘n-1
The term 'n-1' refers to the number of degrees of freedom in a statistical sample. It is used in the denominator when calculating the unbiased estimate of the sample variance. The concept is important because it adjusts the sample variance to correct for the bias that arises from using the sample mean in the calculation. By dividing by 'n-1' instead of 'n', the estimate becomes more representative of the population variance.
πŸ’‘Degrees of freedom
Degrees of freedom in statistics refer to the number of independent values in a dataset that are free to vary. In the context of calculating sample variance, the degrees of freedom are related to the number of data points that can vary without affecting the calculation of the mean. The 'n-1' rule comes from the fact that when calculating the variance from a sample, one degree of freedom is lost because the sample mean is already determined by the sample data.
πŸ’‘Statistic
A statistic is a characteristic or measure derived from a dataset, such as the mean, median, or variance. In the context of this video, the sample mean and sample variance are both statistics calculated from the sample data. The video emphasizes the difference between parameters, which describe the population, and statistics, which describe the sample.
πŸ’‘Parameter
A parameter is a numerical characteristic that describes a population. It is a fixed value within the population and is not subject to sampling variability. In the video, the population mean and population variance are examples of parameters. The video discusses how parameters are estimated from sample statistics, and the importance of using unbiased estimators to accurately represent these population parameters.
πŸ’‘Squared distances
Squared distances are the differences between each data point and a reference value (such as the mean), squared to eliminate negative values and emphasize larger deviations. This concept is central to the calculation of variance, both for a population and a sample. The video script describes how squared distances are used to measure the dispersion of data points around the mean and how this relates to the concept of variance.
Highlights

The video aims to review and build intuition on estimating population variance from a sample.

The population size is denoted by capital N, and the sample size by lowercase n.

The mean of the population is a parameter, denoted by the Greek letter mu (ΞΌ).

The sample mean is calculated similarly to the population mean but is a statistic, denoted by xΜ„.

Variance for a population is calculated by taking the mean of squared distances from the population mean, denoted by σ².

Sample variance can be calculated in different ways, including biased and unbiased estimators.

The biased sample variance is calculated by dividing by the number of data points (n).

An unbiased estimate of population variance is obtained by dividing by n minus 1 (n-1) instead of n.

Dividing by a smaller number (n-1) in the calculation of sample variance yields a larger, unbiased estimate.

The intuition behind using n-1 is that the sample mean is always within the sample and may not accurately represent the population mean.

Sampling may result in a sample mean that is not representative of the true population mean, leading to an underestimation of variance.

The video suggests that a computer program could be developed to further demonstrate the effectiveness of using n-1 for unbiased estimation.

The concept of bias in estimation is introduced, explaining why an unbiased estimator is preferred.

The video emphasizes the importance of understanding the difference between a biased and an unbiased estimate of variance.

The mathematical formulas for calculating population mean, sample mean, population variance, and sample variance are presented.

The video discusses the concept of dispersion in data and how variance measures this.

The video provides a visual example of a population and sample data to illustrate the concepts of mean and variance.

The video aims to clarify common misunderstandings about the calculation of sample variance.

Transcripts

Browse More Related Video

Simulation showing bias in sample variance | Probability and Statistics | Khan Academy

Another simulation giving evidence that (n-1) gives us an unbiased estimate of variance

Statistics: Sample variance | Descriptive statistics | Probability and Statistics | Khan Academy

Sample variance | Descriptive statistics | Probability and Statistics | Khan Academy

Why do we divide by n-1 and not n? | shown with a simple example | variance and sd

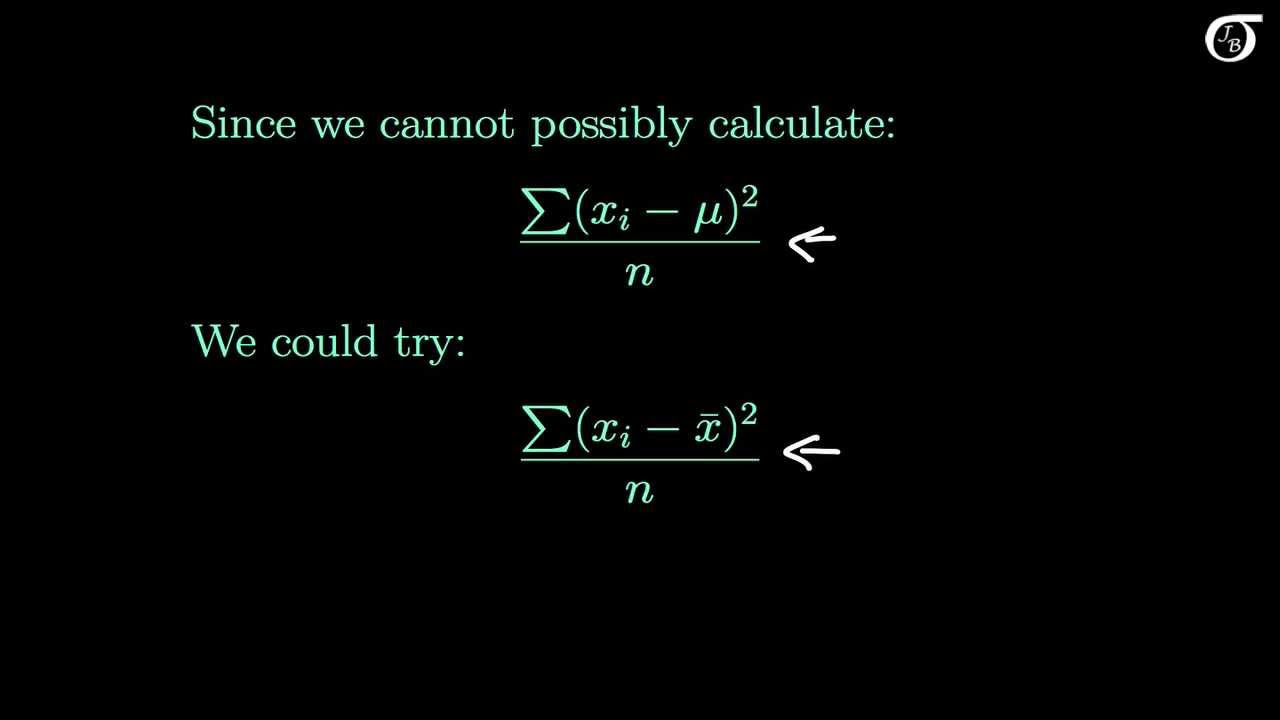
The Sample Variance: Why Divide by n-1?

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Statistical AnalysisVariance EstimationBias CorrectionData InterpretationSample MeanPopulation StatisticsUnbiased EstimatesMathematical IntuitionEducational ContentStatistical Concepts