Proof ols estimator is unbiased

Easynomics
28 Apr 202014:37
EducationalLearning
32 Likes 10 Comments

TLDRThe video script presents a detailed mathematical proof demonstrating that the Ordinary Least Squares (OLS) estimator for the coefficient beta 1 is unbiased. It explains the process of simplifying the formula for beta 1, showing that the expected value of this estimator equals the true value of the parameter. The explanation involves distributing terms, utilizing the properties of summation, and applying the law of iterated expectations. The proof concludes by showing that the bias in the OLS estimator is zero, thus confirming its unbiasedness.

Takeaways
  • 📊 The script discusses the properties of the OLS (Ordinary Least Squares) estimator, specifically its unbiased nature.
  • 🔢 The OLS estimator's expected value is equal to the true value of the parameter, which is a key concept in linear regression analysis.
  • 📈 The process starts by simplifying the formula for beta 1 hat, the estimated coefficient in a linear regression model.
  • 🔄 The summation notation is used to represent the distribution and summing up of terms in the calculation of beta 1 hat.
  • 🧩 The simplification involves recognizing that the summation of deviations of X from its mean equals zero, a crucial step in the proof.
  • 📐 The script explains the law of iterated expectations, which is applied to find the expected value of beta 1 hat.
  • 🤓 The proof involves taking the expectation of the conditional expected value of the error term given X, which is assumed to be zero in the OLS model.
  • 🌟 The script walks through the algebraic manipulation of the OLS formula, highlighting the importance of each step in the process.
  • 🔢 The final result of the analysis confirms that the expected value of beta 1 hat is equal to the true beta 1, thus proving the unbiasedness of the OLS estimator.
  • 📝 The script is an educational resource for understanding the mathematical foundations of linear regression and the properties of OLS estimation.
  • 🎓 The level of detail and step-by-step explanation is beneficial for learners and those looking to deepen their understanding of regression analysis.
Q & A

  • What does OLS estimator's unbiasedness imply?

    -The unbiasedness of the OLS estimator implies that its expected value is equal to the true value of the parameter it estimates.

  • What is the formula for the OLS estimator of beta 1?

    -The OLS estimator of beta 1, denoted as beta 1 hat, is calculated by taking the sum of (X_i - X_bar) times y_i from i=1 to N, and then dividing by the sum of squares of X from i=1 to N.

  • How is the term Y_bar defined in the context of the OLS estimator?

    -Y_bar is defined as the average value of y for all observations, calculated as the sum of y_i divided by the number of observations N.

  • Why is the sum of deviations of X from its mean equal to 0?

    -The sum of deviations of X from its mean is equal to 0 because the summation from i=1 to N of (X_i - X_bar) is essentially the difference between the sum of X_i and N times X_bar, which cancels out since the sum of X_i is n times X_bar.

  • What is the significance of the law of iterated expectations in this context?

    -The law of iterated expectations is crucial in showing that the expected value of beta 1 hat is equal to the true parameter value beta 1. It allows us to take the expectation of the conditional expectation, leading to the conclusion that the bias is 0.

  • How does the OLS assumption affect the expected value of the error term?

    -The fundamental OLS assumption is that the expected value of the error term (u_i) conditional on the X's is 0. This assumption is key to demonstrating that the OLS estimator is unbiased.

  • What happens when we distribute the summation in the OLS estimator formula?

    -Distributing the summation in the OLS estimator formula helps simplify the expression, allowing us to separate and analyze individual terms more effectively, ultimately leading to the demonstration of unbiasedness.

  • What is the role of the denominator in the OLS estimator formula?

    -The denominator in the OLS estimator formula, which is the sum of squares of X, serves as a normalization factor to ensure that the estimated coefficient is not affected by the scale of the X values.

  • How does the simplification of the OLS estimator formula contribute to the proof of unbiasedness?

    -The simplification of the OLS estimator formula, by showing that certain terms cancel out or are equal to zero, helps to isolate the parameter of interest and makes it clear that the expected value of the estimator equals the true parameter value, thus proving its unbiasedness.

  • What is the expected value of the summation of the product of X_i - X_bar and the error term u_i?

    -The expected value of the summation of the product of X_i - X_bar and the error term u_i is 0, given that the error term's expected value conditional on X is 0, as per the OLS assumption.

  • How does the process of taking expectations and applying the law of iterated expectations contribute to the proof?

    -The process of taking expectations and applying the law of iterated expectations allows us to break down the expected value of the OLS estimator into components, which can then be analyzed individually. This step-by-step analysis is crucial for demonstrating that the expected value of the estimator is equal to the true parameter value, thus proving its unbiasedness.

Outlines
00:00
📊 Introduction to OLS Estimator's Unbiasedness

This paragraph introduces the concept of the Ordinary Least Squares (OLS) estimator's unbiasedness, specifically for the parameter beta 1. It explains that the expected value of the OLS estimator should equal the true value of the parameter. The paragraph outlines the process of simplifying the formula for beta 1's estimator by distributing and summing up terms, and highlights the simplification that occurs when recognizing that the mean of the dependent variable (Y bar) is constant across all terms of the summation.

05:05
🔢 Simplified Calculation of Beta 1 Estimator

The paragraph delves into the simplification of the beta 1 estimator formula by recognizing that the summation of deviations of the independent variable (X) from its mean equals zero. It then proceeds to substitute a given linear regression model into the formula and further simplifies the expression. The paragraph emphasizes the importance of understanding the properties of summations and expectations in the context of linear regression analysis.

10:13
🎓 Law of Iterated Expectations and Unbiasedness Proof

This paragraph focuses on applying the law of iterated expectations to prove the unbiasedness of the OLS estimator for beta 1. It explains the steps of taking conditional expectations given X and then the expectations of those conditional expectations to arrive at the expected value of the estimator. The explanation clarifies how the error term's expected value conditional on X's being zero leads to the conclusion that the expected value of the beta 1 estimator is indeed equal to the true value of beta 1, thus demonstrating the unbiasedness of the OLS estimator.

Mindmap
Keywords
💡OLS estimator
The OLS (Ordinary Least Squares) estimator is a statistical method used in linear regression analysis to find the best-fitting line through a set of data points. It minimizes the sum of the squares of the differences (residuals) between the observed values and the values predicted by the model. In the video, the OLS estimator is used to demonstrate its unbiased property, meaning that its expected value equals the true value of the parameter it estimates.
💡Beta 1
Beta 1, often denoted as β1, is the coefficient in a linear regression model that represents the slope of the line. It indicates the change in the dependent variable (Y) for a one-unit change in the independent variable (X). In the context of the video, the unbiased nature of the OLS estimator for Beta 1 is being discussed, showing that the expected value of the estimated Beta 1 is equal to its true value.
💡Expected value
The expected value is a fundamental concept in probability theory that represents the average or mean value of a random variable. It is calculated as the sum of all possible outcomes, each multiplied by its probability. In the video, the expected value is used to demonstrate the unbiased nature of the OLS estimator, showing that the long-term average of the estimator equals the parameter it is designed to estimate.
💡Unbiased
An unbiased estimator is one that, on average, provides the correct value for the parameter it is designed to estimate. In other words, an unbiased estimator has an expected value equal to the true value of the parameter. The video focuses on proving that the OLS estimator for Beta 1 is indeed unbiased, which is a desirable property in statistical estimation.
💡Summation
In mathematics, a summation is a way to represent the addition of a sequence of numbers or terms. It is often denoted with the Greek letter sigma (Σ). In the video, summation is used extensively in the algebraic manipulation of the OLS estimator formula to simplify and prove the unbiased nature of the estimator for Beta 1.
💡Distributed
In the context of the video, 'distributed' refers to the mathematical operation of distributing a common factor across terms within a set of parentheses. This is a step in simplifying expressions, as seen when the term 'Y bar' is distributed across the summation in the formula for the OLS estimator of Beta 1.
💡Sum of squares
The sum of squares is a measure used in statistical analysis, particularly in regression, to quantify the variability or dispersion of a set of data points. It is the sum of the squares of the differences between each data point and the mean of the data set. In the video, the sum of squares of X is used as a denominator in the formula for the OLS estimator of Beta 1.
💡Law of Iterated Expectations
The Law of Iterated Expectations is a fundamental result in probability theory that states the expectation of the conditional expectation of a random variable given another variable is equal to the expectation of the variable itself. This law is applied in the video to prove that the expected value of the OLS estimator for Beta 1 is equal to Beta 1, thus demonstrating its unbiasedness.
💡Error term
The error term, often denoted as 'u' or 'ui' in the context of regression analysis, represents the part of the observed value that is not explained by the independent variables in the model. It is the difference between the actual and predicted values. In the video, it is assumed that the expected value of the error term given the X's is zero, which is a key assumption in the OLS model.
💡Conditional expectation
Conditional expectation is the expected value of a random variable given that another variable takes on a particular value. In the context of the video, the conditional expectation is used to express the expected value of the error term given the values of the independent variable X, which is assumed to be zero according to the OLS model assumptions.
💡Linear regression
Linear regression is a statistical method used to model the relationship between a dependent variable and one or more independent variables by fitting a linear equation to the observed data. In the video, linear regression is the basis for the discussion on the OLS estimator and its properties, specifically focusing on the unbiased estimation of the slope parameter, Beta 1.
Highlights

The OLS estimator for beta 1 is unbiased, meaning its expected value equals the true value of the parameter.

The process begins by simplifying the formula for beta 1 hat by distributing terms and handling summation.

Y bar does not depend on I, allowing for simplification by factoring it out of the summation.

The sum of deviations of X from its mean equals zero, a key property used in the simplification process.

The sum of X is equal to n times X bar, an important relationship derived from the definition of X bar.

The term involving beta naught simplifies to zero due to the properties of summation.

The formula for beta 1 hat is further simplified to involve only the sum of squares of X.

The linear regression equation is used to express Y in terms of beta naught, beta 1, and the error term UI.

The expected value of beta 1 hat is shown to be equal to the expected value of a series of terms involving the error term UI.

The law of iterated expectations is applied to handle the expectation of the conditional expectation of UI given X.

The fundamental OLS assumption that the expected value of the error term given X's is zero is crucial for the proof.

Each term in the summation involving UI is shown to be zero, leading to the conclusion that the expected value of beta 1 hat is beta 1.

The proof demonstrates the unbiased nature of the OLS estimator through a step-by-step mathematical process.

The video content is rich in statistical theory and provides a deep understanding of the properties of the OLS estimator.

The explanation is methodical, making it accessible for viewers to follow along and comprehend the statistical concepts.

The video serves as an educational resource for those interested in econometrics and statistical analysis.

Transcripts

Browse More Related Video

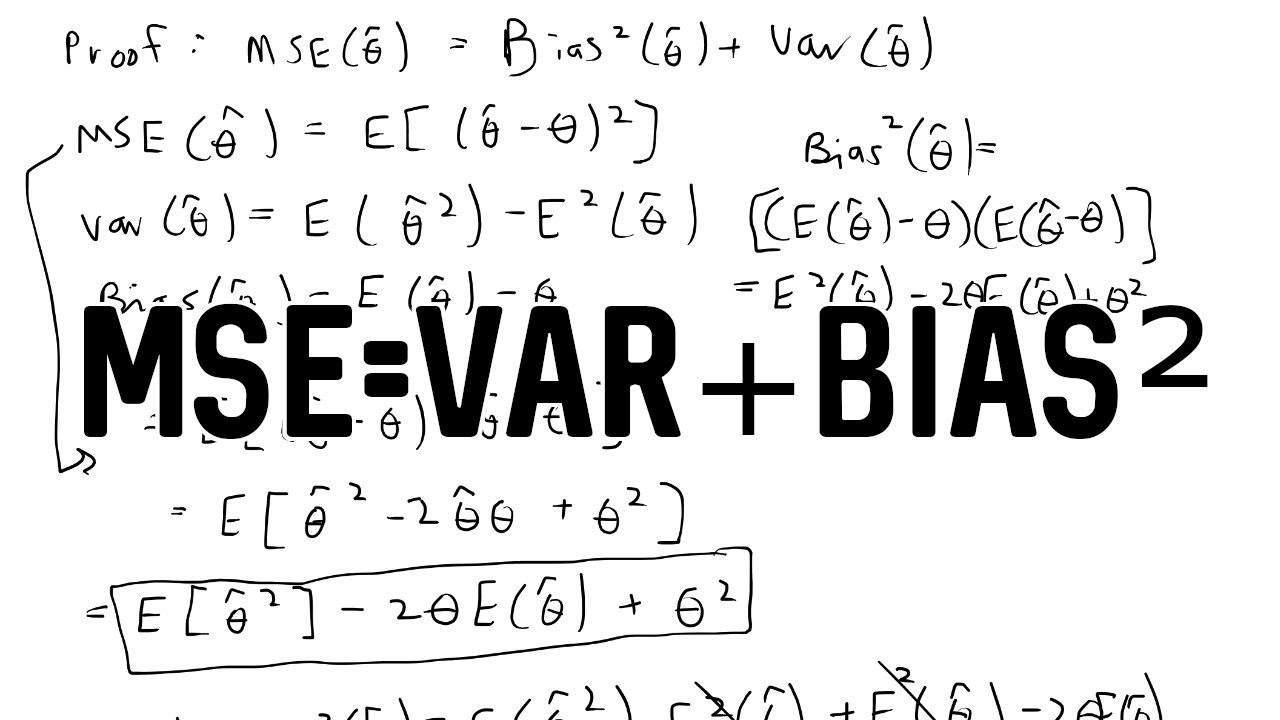
[Proof] MSE = Variance + Bias²

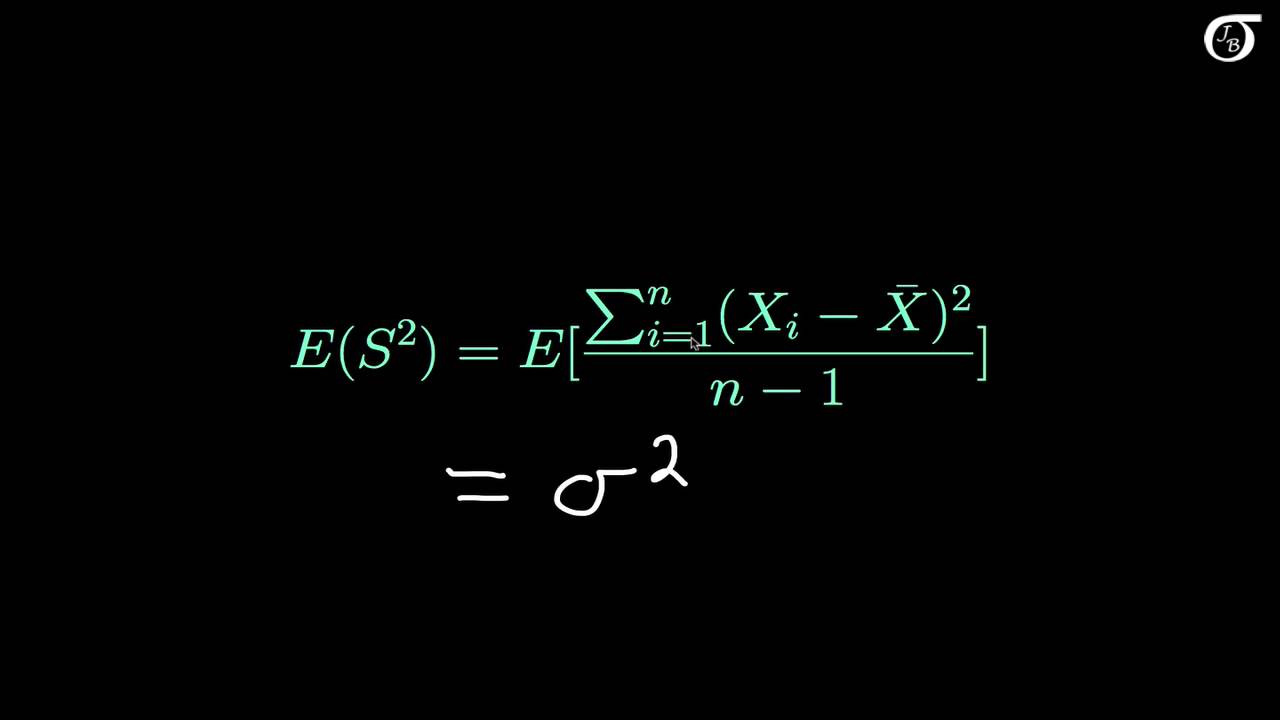
Proof that the Sample Variance is an Unbiased Estimator of the Population Variance

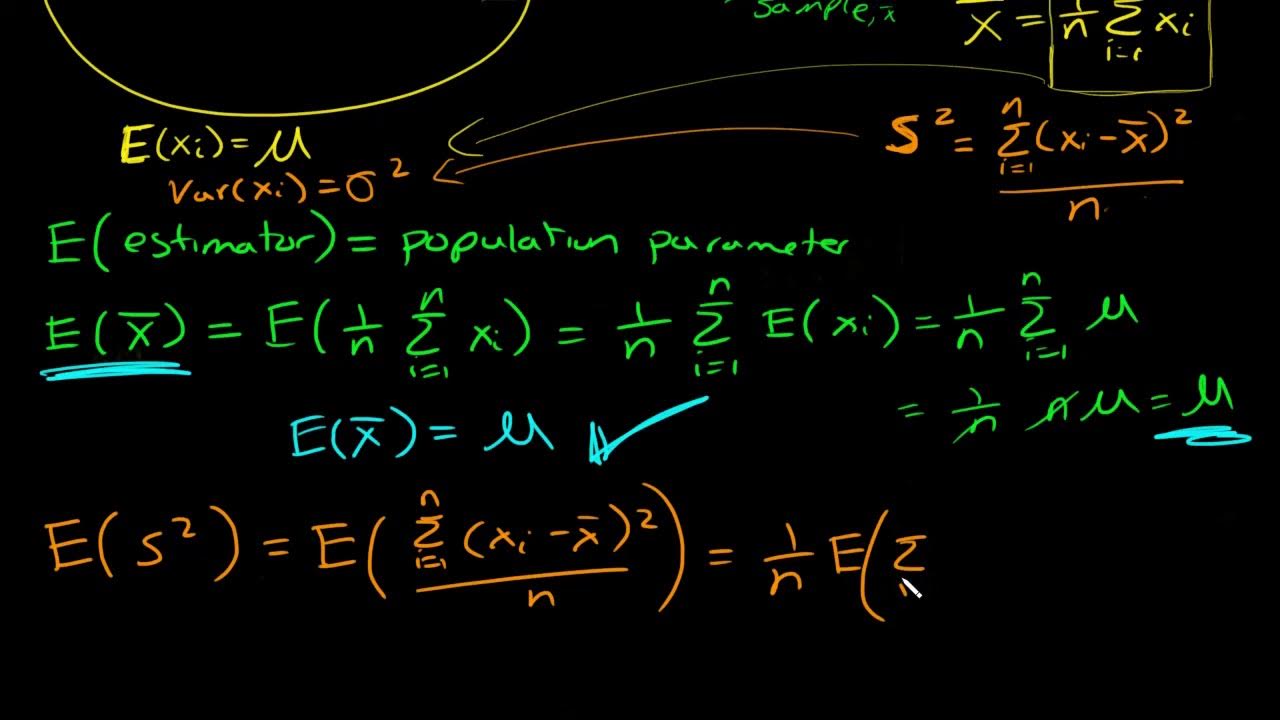
What is an unbiased estimator? Proof sample mean is unbiased and why we divide by n-1 for sample var

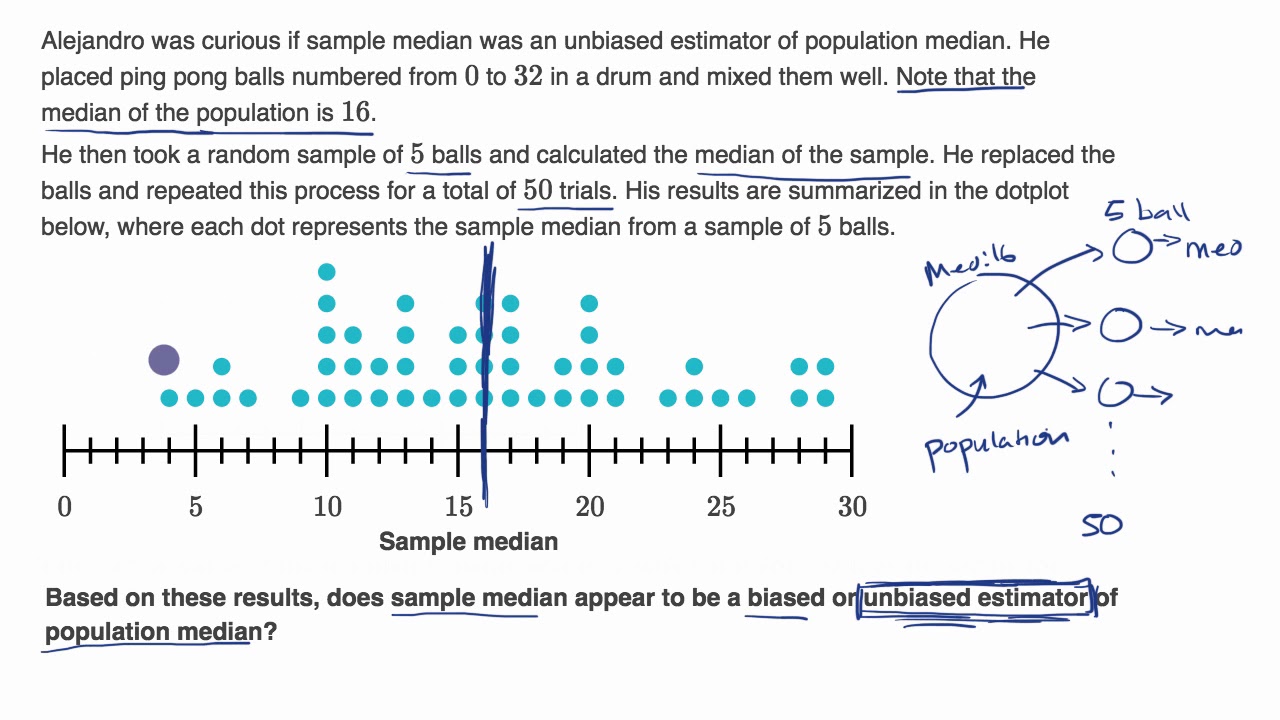
Biased and unbiased estimators from sampling distributions examples

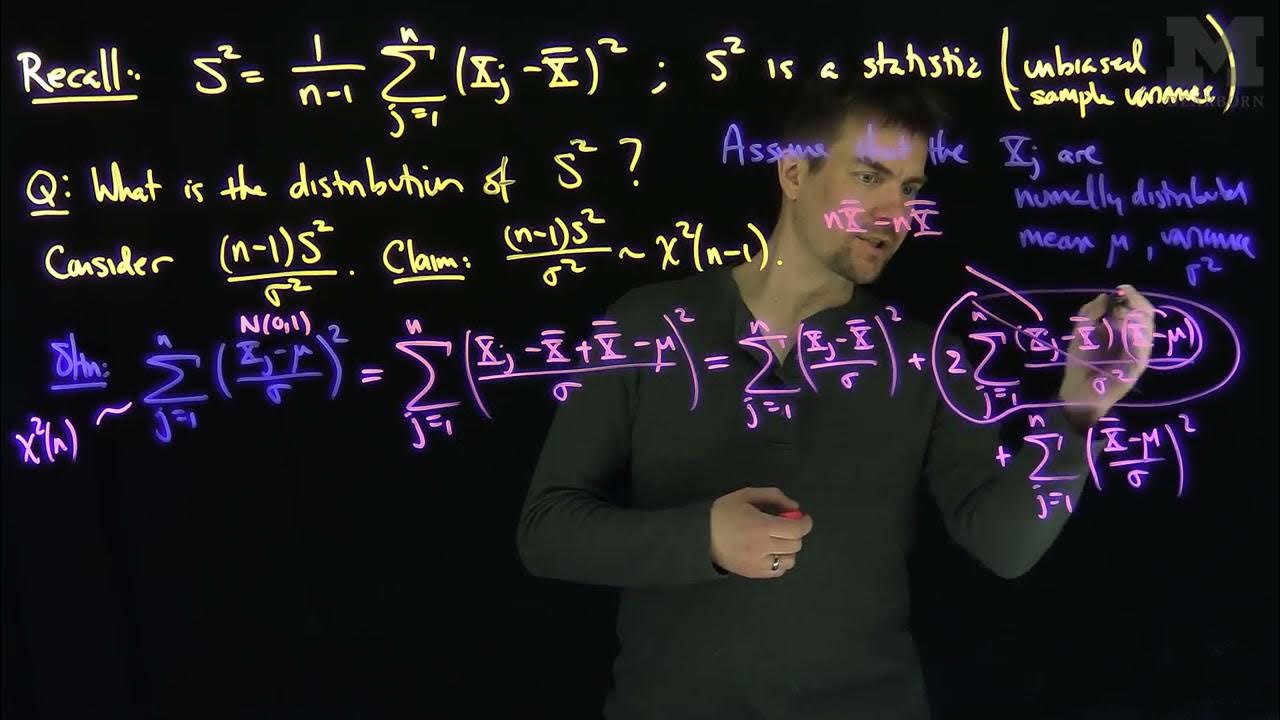
The Sample Variance and its Chi Squared Distribution

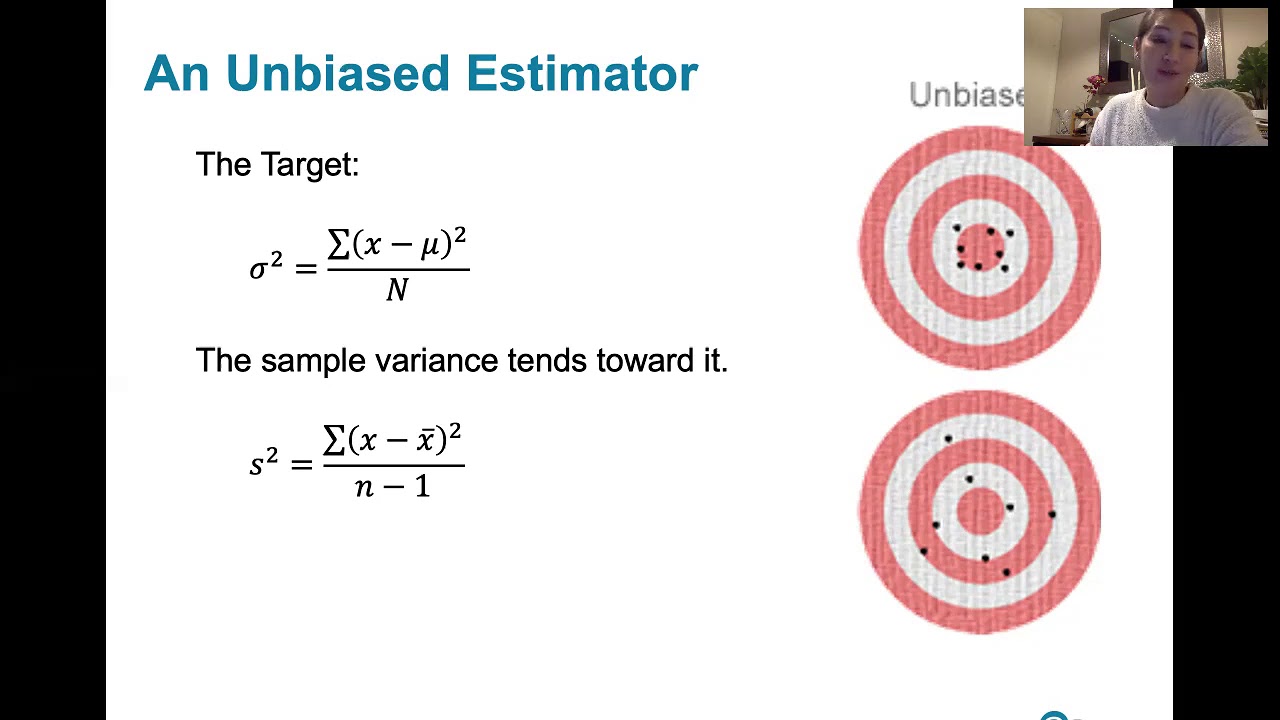
6.3.5 Sampling Distributions and Estimators - Biased and Unbiased Estimators

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
OLS EstimationLinear RegressionStatistical AnalysisParameter EstimationMathematical ProofEconometricsData ScienceUnbiased EstimatorRegression Analysis