Taking the derivative of two binomials using product and chain rule

Brian McLogan
11 Oct 201704:43
EducationalLearning
32 Likes 10 Comments

TLDRThe video script is a detailed explanation of applying the product rule and chain rule in calculus to find derivatives. The speaker starts by discussing the product rule, which involves taking the derivative of the first function times the second function, plus the first function times the derivative of the second. They then delve into the chain rule, emphasizing the importance of identifying the parent and child functions. Using x cubed as an example, the speaker demonstrates how to find the derivative by applying the power rule, substituting the child function, and multiplying by the child function's derivative. The script continues with a step-by-step walkthrough of differentiating more complex functions, such as x cubed minus one to the fourth plus x squared plus five cubed. The speaker also touches on simplification techniques, factoring out common terms like x squared plus five squared and x cubed minus one. The summary concludes by acknowledging the complexity of the problem and suggesting that such intricate factoring is not commonly required in calculus problems.

Takeaways
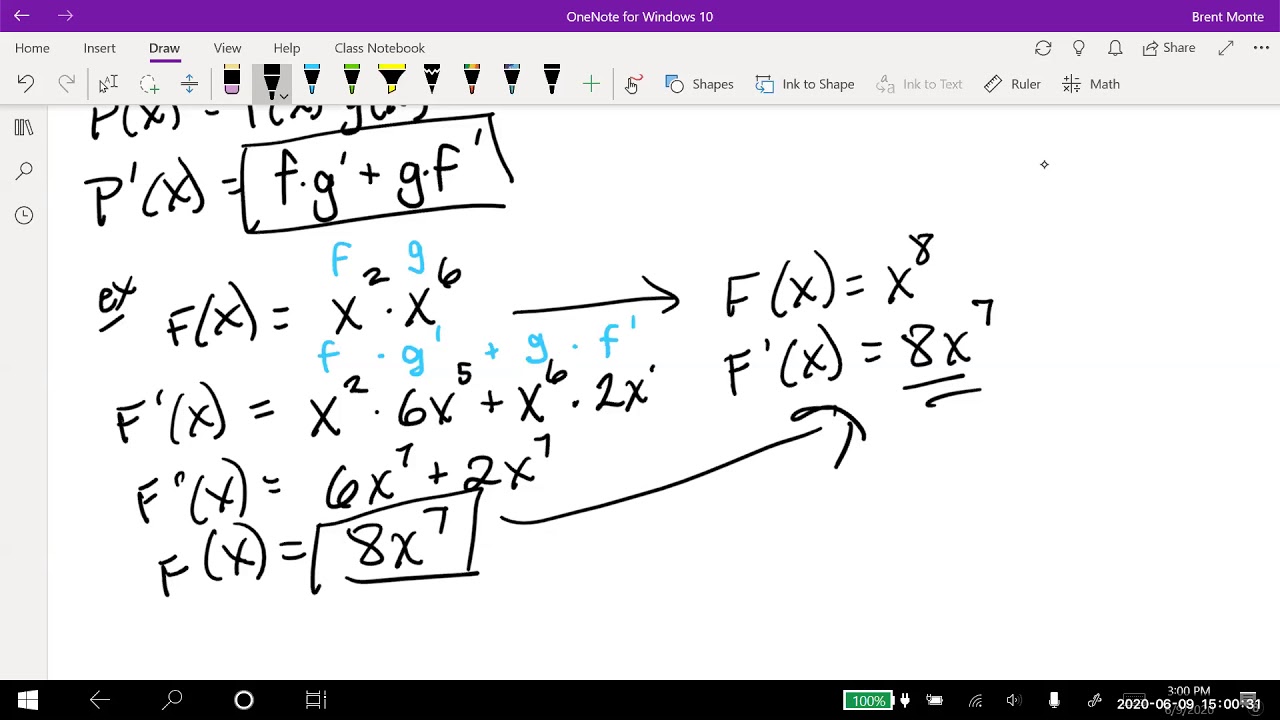
  • 📚 Apply the product rule when taking the derivative of a product of two functions: (f(x) * g(x))' = f'(x) * g(x) + f(x) * g'(x).
  • 🔗 Use the chain rule when taking the derivative of a composition of functions: (f(g(x)))' = f'(g(x)) * g'(x).
  • 👉 Identify the parent function and child function when applying the chain rule.
  • 📈 Find the derivative of the parent function and substitute in the child function.
  • ✖️ Multiply by the derivative of the child function to complete the chain rule application.
  • 🧩 Practice basic chain rule problems to become comfortable with the process.
  • 🔢 For the function x^3, the derivative is 3x^2, obtained by applying the power rule.
  • 🔑 Remember to bring down the coefficient and subtract 1 when applying the power rule.
  • 📉 The derivative of x^2 + 5 is simply 2x.
  • 🔍 Look for common factors in the derivative expression that can be factored out to simplify the expression.
  • ✅ Factor out common terms like x^2 + 5, 3x, and x^3 - 1 to simplify the derivative expression.
  • 📐 After factoring, you may be left with simpler expressions like 4x(x^2 + 5) and 2x^3 - x.
  • 💡 Most calculus problems won't require such complex factoring, but it's good to understand the process for more challenging problems.
Q & A

  • What is the product rule in calculus?

    -The product rule is a fundamental theorem used to find the derivatives of products of two functions. It states that the derivative of a product of two functions is the derivative of the first function times the second function plus the first function times the derivative of the second function.

  • What does the speaker mean by 'applying the chain rule on the derivative'?

    -The speaker is referring to a situation where the derivative of a function itself contains another function, necessitating the use of the chain rule to find the derivative. The chain rule states that the derivative of a composite function is the derivative of the outer function evaluated at the inner function, multiplied by the derivative of the inner function.

  • What is the derivative of x cubed?

    -The derivative of x cubed (x^3) is 3x squared (3x^2), which is found using the power rule for derivatives.

  • How does the speaker simplify the expression involving x squared plus five?

    -The speaker simplifies the expression by factoring out common terms. In this case, they factor out 'x squared plus 5' from the terms where it appears, which helps in simplifying the overall expression.

  • What is the parent function in the context of the chain rule?

    -In the context of the chain rule, the parent function is the outer function in a composite function. It is the function that you apply after the inner function has been evaluated.

  • What is the derivative of x to the fourth power?

    -The derivative of x to the fourth power (x^4) is 4x cubed (4x^3), which is found using the power rule for derivatives.

  • What does the speaker mean by 'taking out' in the context of simplifying the derivative expression?

    -The speaker is referring to factoring out common terms or expressions from the derivative. This is a method of simplification where you identify and remove a common factor from multiple terms to make the expression more manageable.

  • Why is it important to practice basic chain rules?

    -Practicing basic chain rules is important because it helps build a solid foundation in calculus. It ensures that you understand how to handle more complex derivatives that involve nested functions or composite functions.

  • What is the final simplified form of the derivative expression that the speaker is working with?

    -The final simplified form is not explicitly given in the transcript, but the speaker outlines a process of factoring out common terms like 'x squared plus 5', '3x', and 'x cubed minus one'. The exact form would depend on the original functions and the results of the derivatives taken.

  • What is the power rule for derivatives?

    -The power rule for derivatives states that if you have a function of the form f(x) = x^n, where n is a constant, then the derivative f'(x) is n times x to the power of n-1, or f'(x) = n*x^(n-1).

  • How does the speaker suggest visualizing the process of taking derivatives?

    -The speaker suggests visualizing the process by looking at the parent and child functions separately. The parent function is the one that is being multiplied by the child function, and understanding their individual derivatives can help in visualizing the overall process.

  • Why might a problem involving derivatives be difficult to solve without factoring out common terms?

    -A problem involving derivatives can be difficult to solve without factoring out common terms because it can lead to a very complex expression that is hard to manage and simplify. Factoring out common terms helps to reduce the complexity and makes the problem more approachable.

Outlines
00:00
📚 Application of Product and Chain Rules

The paragraph begins with a discussion on the application of the product rule in calculus. The speaker emphasizes the need to take the derivative of the first function and multiply it by the second function, and vice versa. They then highlight the importance of using the chain rule when taking derivatives. The explanation includes visualizing the process to avoid confusion and a step-by-step guide on how to apply the chain rule using parent and child functions. The paragraph concludes with a demonstration of how to simplify expressions by factoring out common terms.

Mindmap
Keywords
💡Product Rule
The product rule is a fundamental principle in calculus used to find the derivative of a product of two functions. It states that the derivative of a product is the derivative of the first function times the second function plus the first function times the derivative of the second function. In the script, the product rule is applied when the speaker mentions 'if I'm going to be applying the product rule, that means I'm going to take the derivative of my first function, times my second function, plus my first function, times the derivative of my second function.'
💡Chain Rule
The chain rule is another essential calculus rule used to compute the derivative of a composite function. It is applicable when a function is made up of two or more functions operating in sequence. The rule states that the derivative of the composite function is the derivative of the outer function evaluated at the inner function, times the derivative of the inner function. The speaker refers to the chain rule when discussing 'applying the chain rule on the derivative' and using it to find the derivative of expressions like 'x cubed'.
💡Derivative
A derivative in calculus represents the rate at which a function changes with respect to its variable. It is a measure of sensitivity to change. The speaker emphasizes the process of taking derivatives multiple times throughout the script, such as 'now I have to take the derivative' and 'the derivative of x squared plus five is just two x.'
💡Parent Function
In the context of composite functions, the parent function refers to the outer function in the sequence. The term is used when the speaker explains the chain rule, indicating that 'my parent function would be x cubed' and later 'the parent function of this one is x to the fourth.'
💡Child Function
The child function is the inner function within a composite function. It is the function that is being operated on by the parent function. The script mentions 'then you re-put in the child function' and 'then I plug in my child function which is x cubed minus 1,' which illustrates the concept of a child function in the application of the chain rule.
💡Power Rule
The power rule is a basic rule in calculus that allows for the differentiation of power functions. It states that the derivative of x to the power of n (where n is a constant) is n times x to the power of n-1. The speaker uses the power rule when finding the derivative of 'x cubed' as '3 squared' and 'x squared' as '2x.'
💡Factoring
Factoring is a mathematical technique used to express an expression as the product of its factors. In the script, the speaker discusses simplifying the derivative by factoring out common terms such as 'x squared plus 5' and 'x cubed minus one.' This is a method to reduce the complexity of the expression and make it easier to work with.
💡Simplifying Expressions
Simplifying expressions involves reducing a mathematical expression to a more straightforward or standard form. The speaker talks about simplifying the derivative by factoring out common terms, which helps in 'taking out so, let's see what they have in common they have a x squared plus 5 square x squared plus 5.'
💡Differentiation
Differentiation is the process of finding the derivative of a function. It is a key concept in calculus and is central to the script's discussion. The speaker is focused on differentiating various functions and applying rules like the product rule and chain rule to do so.
💡Composite Function
A composite function is a function composed of two or more functions. It is typically represented as f(g(x)) or similar forms. The concept is integral to the script as the speaker discusses finding derivatives of composite functions using the chain rule.
💡Visualization
Visualization in mathematics refers to the ability to create a mental or graphical representation of mathematical concepts or operations. The speaker mentions the importance of visualizing the process, especially when dealing with complex derivatives, to avoid confusion and to better understand the steps involved.
Highlights

Applying the product rule to differentiate a function

Taking the derivative of the first function times the second function, plus the first function times the derivative of the second function

Applying the chain rule on the derivative

Visualizing the process to avoid going crazy with calculations

Using parent and child functions in the chain rule

Finding the derivative of x cubed as 3x squared

Multiplying by the derivative of the child function (2x) after applying the power rule

Derivative of x squared plus five is just 2x

Practicing basic chain rules for better understanding

Differentiating x cubed minus one to the fourth plus x squared plus five cubed

Identifying the parent function (x to the fourth) and applying its derivative (4x to the third)

Factoring out common terms to simplify the expression

Factoring out x squared plus 5 squared, 3x, and x cubed minus one

Simplifying the expression to 4x times x squared plus five

Realizing the complexity of the problem and the importance of practice

Not expecting to encounter problems of this difficulty often

Encouraging practice on basic chain rules for better understanding

Transcripts

Browse More Related Video

Product Rule for Derivatives

Chain Rule: the Derivative of a Composition

Math 1325 Lecture 9 5 - Product & Quotient Rule

How to take the derivative with chain rule inside product rule

Product Rule For Derivatives

Logarithmic functions differentiation | Advanced derivatives | AP Calculus AB | Khan Academy

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
CalculusProduct RuleChain RuleDerivativesMathematicsEducationalMath TutorialX CubeSimplifiedFactoringLearning