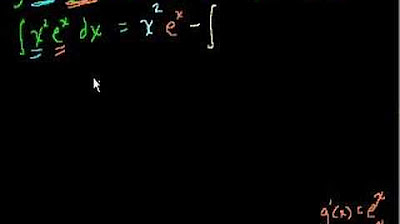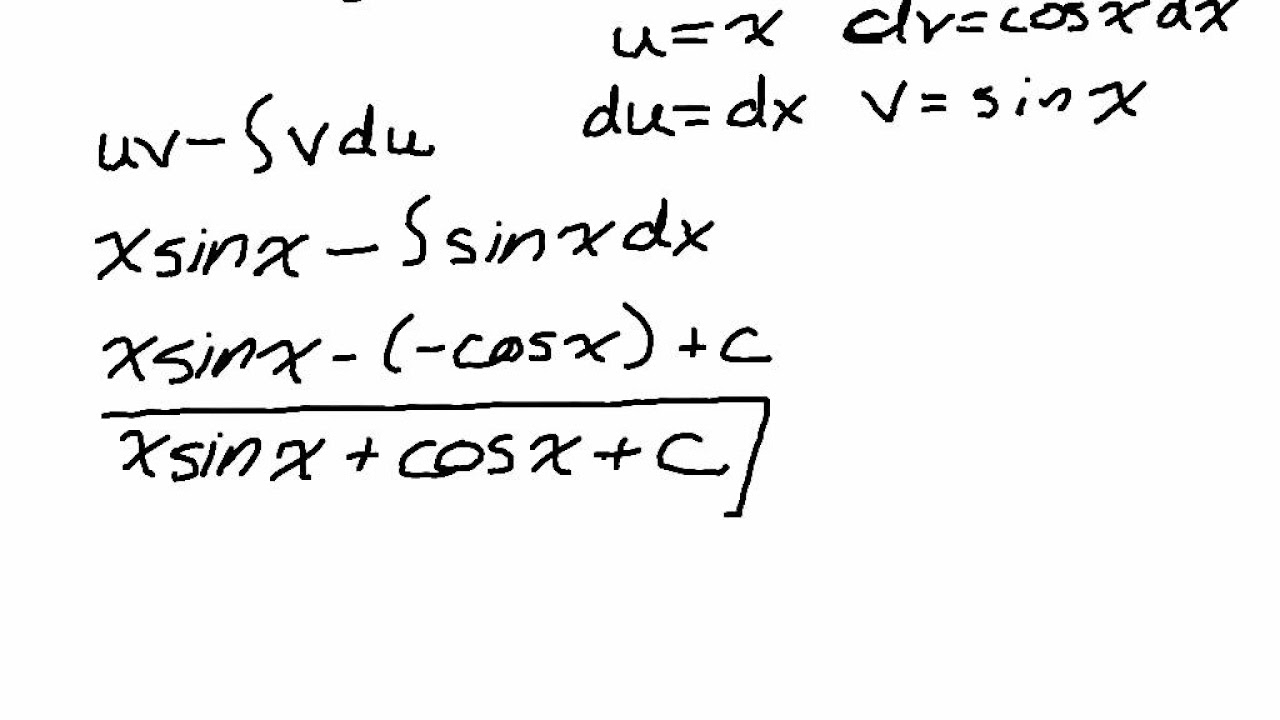Indefinite Integration (part V)
TLDRThe video script discusses the concept of integration by parts, a method for integrating complex functions. It begins by revisiting the product rule of differentiation, then demonstrates how to apply this rule to derive the integration by parts formula. The script provides a clear example by integrating x times the cosine of x, illustrating how to simplify the process by choosing appropriate functions for f(x) and g'(x). The explanation emphasizes the utility of this technique in tackling challenging integrals and offers insights into the thought process behind its application.
Takeaways
- 📚 The concept of 'integration by parts' is introduced as a powerful tool for solving integrals, extending beyond the scope of the exam.
- 🧠 It is emphasized that retaining knowledge of this method is beneficial for becoming proficient in integration techniques.
- 🔄 The product rule of differentiation is reviewed, which is key to understanding integration by parts.
- 🌟 The script demonstrates the process of integrating both sides of an equation, using the product rule as a foundation.
- 📈 By integrating the product rule, a formula for integration by parts is derived, which is useful for solving complex integrals.
- 🤔 The speaker clarifies the arbitrary nature of the formula and its application, showing how it can be applied to indefinite integrals as well.
- 🌐 An example is given where the indefinite integral of 'x cosine of x' is tackled using integration by parts, as traditional methods fail.
- 🔄 The process of choosing functions for 'f(x)' and 'g' (or their derivatives) is explained, with a preference for simplifying the derivative.
- 📊 The example illustrates the simplification of the integral through the application of integration by parts, leading to a more manageable form.
- 📚 The antiderivative of 'cosine of x' is identified as 'sine of x', and the importance of memorizing basic calculus relationships is highlighted.
- 🔍 The final result of the example demonstrates the power of integration by parts in simplifying complex integrals and the necessity of including the constant 'c'.
- 📅 The speaker promises to cover more examples of using integration by parts in the next presentation, indicating its importance in solving advanced integrals.
Q & A
What is the main topic discussed in the transcript?
-The main topic discussed in the transcript is integration by parts, a method used to solve complex integrals.
How does the speaker introduce the concept of integration by parts?
-The speaker introduces integration by parts by first discussing the product rule of differentiation and then showing how integrating both sides of the product rule equation leads to the integration by parts formula.
What is the product rule of differentiation mentioned in the transcript?
-The product rule of differentiation mentioned in the transcript is the operation where if you have two functions, f(x) and g(x), the derivative of their product [f(x)*g(x)] is the derivative of the first function times the second function plus the first function times the derivative of the second function.
How does the speaker simplify the example integral of x*cos(x)dx?
-The speaker simplifies the integral of x*cos(x)dx by applying the integration by parts formula, choosing x as f(x) and cos(x) as g'(x), which leads to the antiderivative of cos(x), sine(x), and then performing the integration to get x*sin(x) - integral of sine(x)dx, which simplifies to x*sin(x) + cos(x) + C.
Why does the speaker choose x as f(x) and cos(x) as g'(x) in the example?
-The speaker chooses x as f(x) and cos(x) as g'(x) because taking the derivative of x simplifies to 1*g(x), which is easier to handle, and the antiderivative of cos(x) is sin(x), which is no more complicated than the original function.
What is the significance of the formula derived from the product rule in the transcript?
-The significance of the formula derived from the product rule is that it serves as the foundation for integration by parts, allowing the simplification and solving of more complex integrals that do not fit into other integration techniques like substitution or simple antidifferentiation.
What does the speaker suggest about memorizing the integration by parts formula?
-The speaker suggests that while memorizing the integration by parts formula can be helpful, especially for exams, it is also possible to derive it from the product rule, which can be a more intuitive approach and does not require memorization.
How does the speaker plan to proceed in the next presentation?
-In the next presentation, the speaker plans to provide multiple examples demonstrating the use of integration by parts to solve more complex integrals.
What is the role of the antiderivative in the process of integration?
-The antiderivative plays a crucial role in the process of integration as it represents the reverse operation of differentiation. It is used to find the original function from its derivative, which is the goal of integration.
Why is the process of moving from a complicated expression to a simpler one important in mathematics?
-The process of moving from a complicated expression to a simpler one is important in mathematics because it allows for easier computation, better understanding of the problem, and often leads to more manageable or insightful forms that can be used to solve the given mathematical issue.
What is the significance of the 'plus C' at the end of the integrated expression?
-The 'plus C' at the end of the integrated expression represents the constant of integration, which is necessary because the antiderivative of a function is not unique; it can be shifted by any constant value without changing the derivative.
Outlines
📚 Introduction to Integration by Parts
This paragraph introduces the concept of Integration by Parts, a method for integrating complex functions. It begins by discussing the importance of understanding different types of integrals and retaining this knowledge beyond the context of an exam. The speaker then revisits the Product Rule for differentiation, leading into an explanation of how Integration by Parts is derived from it. The process involves integrating both sides of an equation and rearranging terms to simplify the integral. The speaker emphasizes the utility of this method, especially when dealing with more sophisticated integrals, and sets the stage for demonstrating its application in the subsequent presentation.
🔍 Applying Integration by Parts to a Specific Example
In this paragraph, the speaker delves into a specific example to illustrate the application of Integration by Parts. The example chosen is the integral of x times the cosine of x. The speaker explains why certain functions are chosen for f(x) and g'(x) in the formula, highlighting the simplification that occurs when the derivative of f(x) is taken and the antiderivative of g'(x) is known. The explanation includes a step-by-step breakdown of the process, leading to the simplification of the integral and the eventual derivation of the result. The speaker also discusses the intuition behind choosing certain functions for integration by parts and the importance of memorizing this formula for exams, while emphasizing the underlying connection to the Product Rule.
Mindmap
Keywords
💡Integral
💡Product Rule
💡Chain Rule
💡Integration by Parts
💡Antiderivivative
💡Derivative
💡Indefinite Integral
💡Definite Integral
💡Substitution
💡Sine and Cosine Functions
Highlights
The concept of 'integration jock' is introduced, implying the proficiency in integration techniques.
The transcript discusses the retention and application of integral techniques beyond the exam context.
A review of the product rule of differentiation is provided, emphasizing its importance in understanding integration.
The chain rule is explained in the context of taking the derivative of a product of two functions.
The process of integrating both sides of an equation is discussed, highlighting its role in reverting to the original functions.
The concept of indefinite integral and its relation to antiderivatives is touched upon.
The term 'integration by parts' is introduced as a method for solving complex integrals.
The usefulness of integration by parts is explained, especially for complex integrals that do not fit into simpler integration techniques.
The process of choosing functions for integration by parts is discussed, emphasizing the simplification of the integral.
An example of integrating a complex function (x cosine of x) using integration by parts is provided.
The selection of u and dv in integration by parts is rationalized based on the simplicity of their derivatives and antiderivatives.
The solution to the integral of x cosine of x is derived using integration by parts.
The antiderivative of cosine of x is identified as sine of x, which is used in the integration by parts method.
The importance of remembering the relationship between the derivative and antiderivative of functions is emphasized.
Integration by parts is presented as a derivation from the product rule, offering a fresh perspective on its application.
The transcript concludes with a mention of future presentations focusing on practical examples of integration by parts.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: