Worked example: Continuity at a point | Limits and continuity | AP Calculus AB | Khan Academy

Khan Academy

11 Jul 201607:18

EducationalLearning

32 Likes 10 Comments

TLDRThe video script discusses the concept of limits in calculus, specifically focusing on the function g(x). It explores whether the right and left-hand limits exist as x approaches six and three, respectively. The analysis involves examining the graph of the function and determining the behavior of the function as it approaches these points from both directions. The conclusion is that the limit does not exist at x equals six due to unbounded behavior from the left and an undefined value at x equals six, indicated by a vertical asymptote. However, at x equals three, the function is defined and the one-sided limits exist, though the actual limit does not due to differing values from the left and right approaches.

Takeaways

📈 The script discusses the analysis of a graph of the function y = g(x) and the verification of certain mathematical statements related to limits and continuity.
🔍 The process of evaluating the existence of one-sided limits as x approaches specific values is described, emphasizing the need to consider values from both the right and left-hand sides.
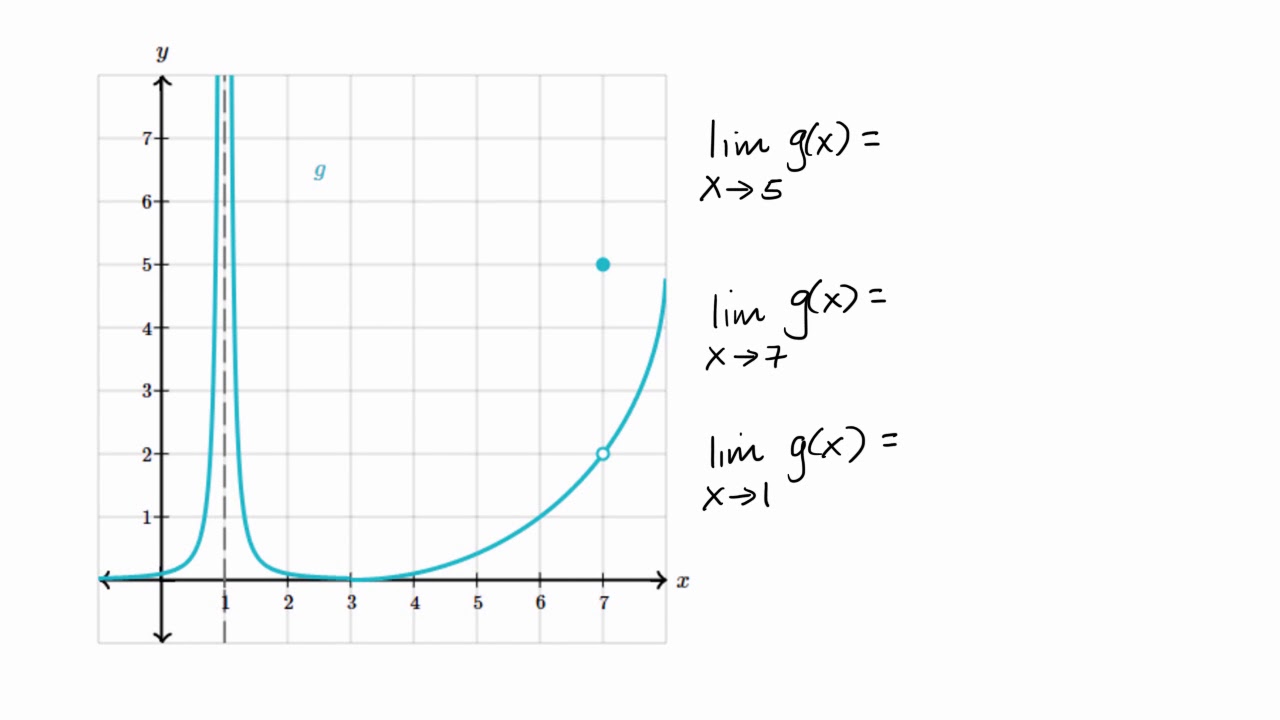
📌 For x approaching 6, the right-hand side limit appears to exist and is close to negative three, while the left-hand side limit does not exist, as it seems to approach infinity.
🚫 The limit of g(x) as x approaches 6 is concluded to not exist, as the left-hand side limit does not exist, and for a limit to exist, both sides must converge to the same value.
❌ The function g(x) is not defined at x equals 6, as indicated by an open circle on the graph, and a vertical asymptote at x equals 6.
🔄 At x equals 3, there is a jump discontinuity, and the function is not continuous due to the lack of an existing limit at that point.
📈 The right-hand side limit as x approaches 3 from the right exists and is equal to negative two, while the left-hand side limit approaches two.
🔄 The function g(x) is defined at x equals 3, as indicated by a solid dot on the graph, but the function is not continuous at that point because the limit does not exist there.
📊 The script encourages viewers to pause the video and attempt to work through the problems independently, promoting active learning and problem-solving skills.
🌟 The importance of understanding the formal definition of limits and the conditions required for a function to be considered continuous is emphasized throughout the script.

Q & A

What is the first statement being evaluated in the transcript?
-The first statement being evaluated is whether both the limit of g(x) as x approaches six from the right-hand side and the limit as x approaches six from the left-hand side exist.
How does the speaker determine if the limit from the right-hand side of g(x) as x approaches six exists?
-The speaker determines the limit from the right-hand side by examining the values of g(x) as x takes on values greater than six, such as g(9), g(8), g(7), etc., and observing their trends and proximity to negative three.
What conclusion does the speaker reach about the limit from the right-hand side of g(x) as x approaches six?
-The speaker concludes that the limit from the right-hand side exists because the values of g(x) approach negative three as x gets closer to six from the right.
How does the speaker determine if the limit from the left-hand side of g(x) as x approaches six exists?
-The speaker examines the values of g(x) as x takes on values less than six, such as g(3), g(4), g(5), etc., and observes their trends, noting that they appear to be unbounded and approach infinity as x gets closer to six from the left.
What is the speaker's conclusion about the limit from the left-hand side of g(x) as x approaches six?
-The speaker concludes that the limit from the left-hand side does not exist because the values of g(x) approach infinity rather than a specific value as x approaches six.
What does the speaker say about the continuity of g(x) at x equals six?
-The speaker states that g(x) is not continuous at x equals six because the limit does not exist at that point, the function is not defined at x equals six, and the value of the function is not equal to the value of the limit.
What is the second statement being evaluated in the transcript?
-The second statement being evaluated is whether both the right-hand and left-hand limits of g(x) as x approaches three exist.
What does the speaker find when evaluating the limit from the right-hand side of g(x) as x approaches three?
-The speaker finds that the limit from the right-hand side exists and approaches negative two as x gets closer to three from values greater than three.
What does the speaker find when evaluating the limit from the left-hand side of g(x) as x approaches three?
-The speaker finds that the limit from the left-hand side exists and approaches two as x gets closer to three from values less than three.
Does the speaker conclude that g(x) is continuous at x equals three based on the script?
-No, the speaker concludes that g(x) is not continuous at x equals three because although the function is defined at that point, the limit does not exist there.
What is the significance of the open circle and the vertical asymptote in the graph as discussed in the transcript?
-The open circle at x equals six signifies that g(x) is not defined at that point, and the vertical asymptote indicates a discontinuity where the function goes to infinity or is undefined at that value.

Outlines

00:00

📊 Analyzing Limits from Both Sides

This paragraph discusses the process of evaluating the existence of limits for a given function g(x) at a specific point, in this case, x=6. The voiceover explains the concept of one-sided limits, emphasizing the need for both the left-hand and right-hand limits to exist and be equal for the overall limit to be valid. It is determined that the right-hand limit exists and approaches a value between negative three and negative four, while the left-hand limit does not exist due to the function approaching infinity. The voiceover also clarifies that the limit at x=6 cannot be said to exist, as the left-hand limit is undefined, and the function g(x) is not continuous at x=6 due to the presence of a vertical asymptote and the function's value not matching the limit value.

05:01

🔍 Evaluating Continuity and One-Sided Limits at x=3

The focus of this paragraph is on the evaluation of the function's continuity and one-sided limits at x=3. The voiceover begins by examining the right-hand limit as x approaches 3, noting that it exists and approaches negative two. It then considers the left-hand limit, which also exists and approaches the value of two. Despite both one-sided limits existing, the overall limit at x=3 does not exist because the left and right limits are not equal. The paragraph further discusses the definition of the function at x=3, indicated by a solid dot on the graph, confirming that the function is indeed defined at this point. However, the function is not continuous at x=3 since the limit does not exist at this point, leading to the conclusion that the function is discontinuous.

Mindmap

Keywords

💡limit

In the context of the video, a limit refers to the value that a function approaches as the input (x-value) gets arbitrarily close to a certain point. It is a fundamental concept in calculus that helps in understanding the behavior of functions, especially at points of discontinuity or at infinity. The video script discusses the left-hand limit and right-hand limit of the function g(x) as x approaches specific points, such as six and three, to determine the function's behavior and continuity at those points.

💡function

A function, as discussed in the video, is a mathematical relation that pairs each element from a set (domain) with exactly one element from another set (range). In this case, the function is denoted as g(x), and the video focuses on analyzing its graph and behavior at specific points and values. Functions are a core concept in mathematics and are used to model various real-world scenarios and relationships.

💡graph

The graph in the video refers to the visual representation of the function g(x), where the x-values are plotted on a horizontal axis and the corresponding y-values (g(x)) on a vertical axis. Graphs are essential tools in mathematics for visualizing and understanding the behavior and properties of functions, such as trends, patterns, and points of interest like maxima, minima, and discontinuities.

💡discontinuity

A discontinuity in the video script indicates a point at which the function g(x) is not continuous. Specifically, it refers to points where the function is not defined, or where the left-hand limit and right-hand limit do not match. Discontinuities are crucial in the study of functions as they can affect the function's differentiability and integrability, and they often signify abrupt changes or breaks in the function's graph.

💡right-hand side

The term 'right-hand side' in the video script refers to the approach to a certain x-value from values greater than that x-value. For example, when discussing the limit of g(x) as x approaches six from the right-hand side, it means evaluating what g(x) tends to do as x increases towards, but never reaches, six. This is a critical concept in understanding one-sided limits, which are essential in the analysis of functions, particularly at points of discontinuity.

💡left-hand side

The 'left-hand side' in the video script refers to the approach to a certain x-value from values less than that x-value. For instance, when examining the limit of g(x) as x approaches six from the left-hand side, it involves looking at the behavior of g(x) as x decreases towards six. One-sided limits are crucial for understanding the behavior of functions at points where the function may not be defined or where the behavior changes abruptly.

💡asymptote

An asymptote in the context of the video is a line that the graph of the function g(x) approaches but never actually intersects or crosses. It represents a vertical or horizontal line that the function tends towards, indicating the behavior of the function at large values or at certain points. Asymptotes are significant in the study of functions as they provide insight into the long-term behavior of the function and can affect its properties, such as boundedness.

💡infinity

In the video, 'infinity' refers to a concept where the value of the function g(x) grows without bound as x approaches a certain value. It is a crucial concept in mathematics, representing a quantity that is greater than any real number. The video discusses the behavior of the function as x approaches six from the left-hand side, where the function's value appears to approach infinity, indicating that the limit at that point does not exist.

💡continuous

The term 'continuous' in the video script refers to a property of the function g(x) where there are no abrupt changes, breaks, or gaps in the graph. A function is considered continuous at a point if it is defined at that point, the limit exists, and the value of the function equals the limit. The video examines the continuity of g(x) at specific points, such as x equals six and three, to determine the function's behavior and properties.

💡defined

In the context of the video, 'defined' means that the function g(x) has a specific, unambiguous value for a given x-value. The video discusses points where the function is not defined, such as x equals six, where there is a vertical asymptote, and the function does not have a value, indicated by an open circle on the graph. Understanding where a function is defined is essential for analyzing its continuity, limits, and overall behavior.

💡value of the function

The 'value of the function' refers to the output of the function g(x) for a given input x-value. In the video, the values of the function at different x-values are used to analyze the function's behavior, particularly when approaching points of interest such as x equals six and three. The video examines whether these function values approach specific limits and whether they match the limits to determine continuity and the function's properties.

Highlights

The task involves analyzing a graph of the function y = g(x) and determining the truth of certain statements about its limits.

The first statement examines the existence of limits as x approaches six from both the right and left sides.

The right-hand limit appears to exist and is close to negative three when approaching six from values greater than six.

The left-hand limit does not exist as the function appears to approach infinity when x gets closer to six from the left.

The overall limit as x approaches six does not exist because the left-hand limit does not exist.

The function g(x) is not defined at x equals six, as indicated by an open circle on the graph.

The function is not continuous at x equals six due to the function's value not equaling the limit and the existence of a vertical asymptote.

The next statement discusses the existence of right-hand and left-hand limits as x approaches three.

The right-hand limit as x approaches three from the right exists and is approaching negative two.

The left-hand limit also exists and is approaching two as x gets closer to three from the left.

Despite both one-sided limits existing, the function is not continuous at x equals three since the limits do not equal each other.

The function g(x) is defined at x equals three, as indicated by a solid dot on the graph.

The function's continuity at x equals three is not possible because the one-sided limits do not match.

The process of analyzing the graph and determining the existence and non-existence of limits is demonstrated through a step-by-step approach.

The concept of limits and continuity is applied to specific values of x within the function's domain.

The graphical representation of the function provides insights into the behavior of the function near specific points.

The existence of vertical asymptotes and their impact on the function's continuity are discussed.

The importance of one-sided limits in determining the continuity of a function at a particular point is emphasized.

Transcripts

Browse More Related Video

Limit at a point of discontinuity

Analyzing functions for discontinuities (discontinuity example) | AP Calculus AB | Khan Academy

One-sided limits from tables | Limits and continuity | AP Calculus AB | Khan Academy

BusCalc 03 Estimating Limits from Tables

BusCalc 02 Limits and Continuity

Limits from graphs | Limits and continuity | AP Calculus AB | Khan Academy

Worked example: Continuity at a point | Limits and continuity | AP Calculus AB | Khan Academy

Takeaways

Q & A

What is the first statement being evaluated in the transcript?

How does the speaker determine if the limit from the right-hand side of g(x) as x approaches six exists?

What conclusion does the speaker reach about the limit from the right-hand side of g(x) as x approaches six?

How does the speaker determine if the limit from the left-hand side of g(x) as x approaches six exists?

What is the speaker's conclusion about the limit from the left-hand side of g(x) as x approaches six?

What does the speaker say about the continuity of g(x) at x equals six?

What is the second statement being evaluated in the transcript?

What does the speaker find when evaluating the limit from the right-hand side of g(x) as x approaches three?

What does the speaker find when evaluating the limit from the left-hand side of g(x) as x approaches three?

Does the speaker conclude that g(x) is continuous at x equals three based on the script?

What is the significance of the open circle and the vertical asymptote in the graph as discussed in the transcript?