One-sided limits from tables | Limits and continuity | AP Calculus AB | Khan Academy
TLDRThis instructional video explores the concept of limits in calculus, focusing on how to estimate the limit of a function as it approaches a specific point from one direction. The instructor clarifies the notation for approaching a value from the left or right and uses a table of selected function values to illustrate the process. Through examples, viewers learn to estimate limits as x approaches 1 from the left and as x approaches -2 from the left, highlighting the difference between limits existing at a point and when they may not exist due to unbounded behavior. This video demystifies limit calculations, providing a foundation for understanding more complex calculus concepts.
Takeaways
- 📚 The concept of limits is introduced as a mathematical tool to understand the behavior of functions as the input approaches a certain value.
- 👉 When approaching a value 'a' from the left, it is denoted as 'X approaches a from the left', which means considering values less than 'a'.
- 🔍 To estimate a limit, focus on the values of the function as X gets closer to the point of interest from the specified direction, ignoring the value at the point itself if it's not the direction of approach.
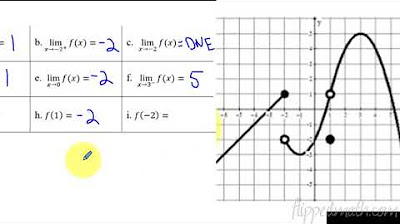
- 📈 The video provides an example where the function F of X approaches 2 as X approaches 1 from the left, based on the given table of values.
- 📊 In another example, as X approaches -2 from the left, the function F of X seems to become unbounded, suggesting that the limit does not exist in this case.
- 🤔 It's important to distinguish between approaching a point from the left and from the right, as the limit may not be the same from both directions.
- 🌟 The limit of a function at a point may not necessarily equal the function's value at that point.
- ⚠️ When solving limit problems, it's crucial to interpret the negative superscript correctly to understand the direction from which the limit is being approached.
- 📝 In multiple-choice questions, choose the most reasonable estimate based on the data provided, even if the exact value is not given.
- 💡 The video script serves as a tutorial to guide students in understanding and estimating limits of functions by analyzing the behavior of the function as it approaches specific values.
Q & A
What does the notation 'X approaches one from the left' signify?
-The notation indicates approaching the value of one from values less than one, specifically from the left side on a number line.
Why is it important not to confuse the negative superscript in 'X approaches one from the left' with a negative number?
-The negative superscript indicates direction (from the left) rather than the sign of the number, so it's critical to understand it represents values less than one, not negative one.
How can you estimate the limit of F of X as X approaches one from the left using a table?
-By observing values of F of X for X values increasingly close to one from the left and noting the trend or value F of X is approaching.
Why might the limit of F of X as X approaches a point differ from the actual value of F of X at that point?
-Limits focus on the value that F of X approaches as X gets arbitrarily close to a point, which might differ from F of X's value exactly at that point due to discontinuities or other behaviors.
What does it mean if the limit of F of X as X approaches a value from the left is a whole number?
-It suggests that as X gets infinitely close to the value from the left, F of X approaches a specific, constant value, in this case, a whole number.
What does 'unbounded' mean in the context of limits?
-Unbounded refers to a function's value increasing or decreasing without limit as X approaches a specific point, indicating the function does not settle towards a finite value.
What does it imply if the limit of F of X as X approaches negative two from the left does not exist?
-It implies that as X approaches negative two from the left, F of X does not approach a specific value but rather increases or decreases without bound, indicating no finite limit exists.
How can the behavior of F of X as X approaches negative two from the right provide insight into the function's limit?
-Observing F of X as X approaches negative two from the right helps determine if F of X approaches a specific value from that direction, offering insight into the function's continuity and limit behavior.
Why is it significant to consider limits from both the left and the right when evaluating a function's limit at a point?
-Evaluating limits from both directions ensures understanding of the function's behavior around a point, as differing left and right limits indicate discontinuity or a non-existent overall limit at that point.
What conclusion can be drawn if F of X approaches different values from the left and right as X approaches a specific point?
-If F of X approaches different values from the left and right, it suggests the limit at that point does not exist, indicating a discontinuity or break in the function at that point.
Outlines
📚 Understanding Limits from the Left
This paragraph discusses the concept of limits in calculus, specifically focusing on how to estimate the limit of a function F as the variable X approaches a certain value from the left side. The instructor clarifies that the negative superscript next to the number 1 does not indicate negative one, but rather signifies the limit from the left approach. The paragraph emphasizes the importance of not being distracted by the function's value at the point of interest and instead focusing on the behavior of the function as it gets closer to the point. By examining the given table of values, the instructor illustrates that the function F appears to approach the value of 2 as X gets closer to 1 from the left, although it is stressed that this is an estimate and the actual value could be slightly different. The concept is further reinforced by another example where the function F approaches negative two from the left, and it is observed that the function values become increasingly negative, suggesting that the limit is unbounded.
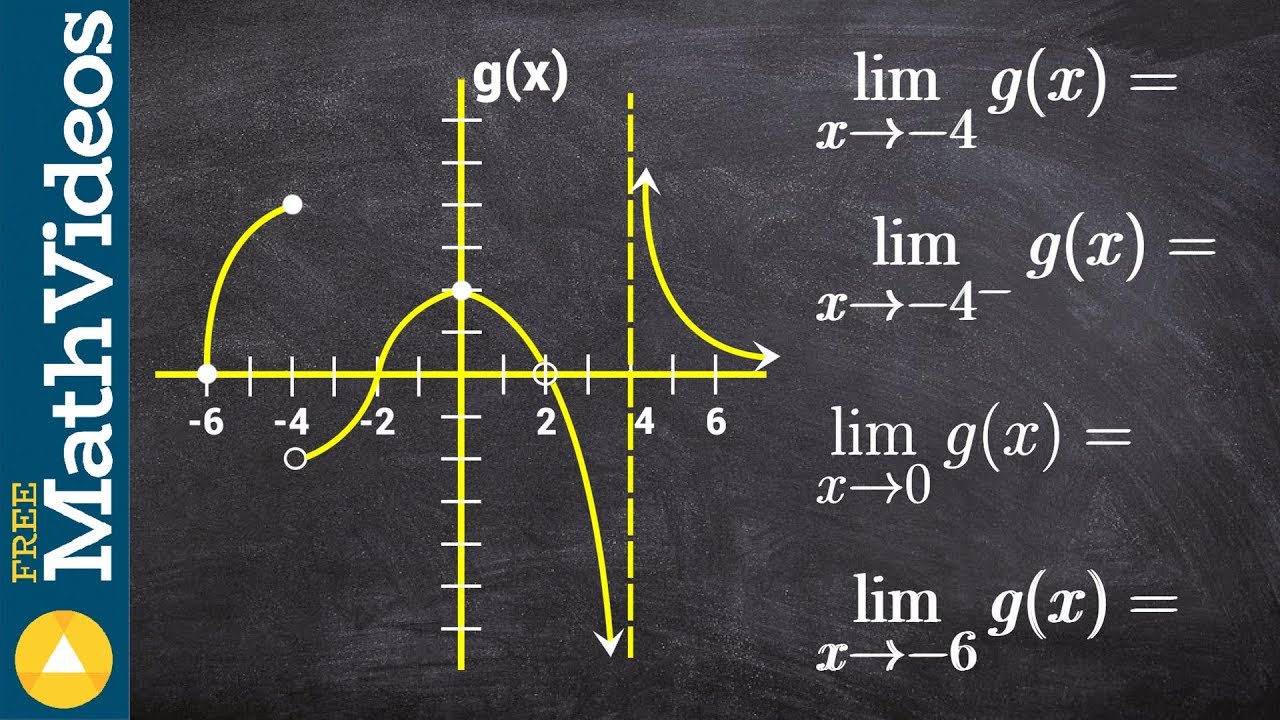
🔢 Estimating Limits from the Right
In this paragraph, the discussion continues with the concept of limits, but this time focusing on the behavior of the function F as X approaches a value from the right side. It highlights the importance of considering the direction from which X approaches the point of interest, as it can significantly affect the limit's estimation. The instructor uses the provided table to analyze the function's values as X gets closer to negative two from the right. Unlike the left approach, where the function values were unbounded and negative, the right approach shows a different behavior. The function F values become closer to negative four as X approaches negative two from the right, which is the same as the function's value at negative two. The paragraph concludes by noting that if the limit from the left and the right approaches are different, it indicates that the function does not have a limit at that point. This is a crucial concept in understanding the behavior of functions and their limits from different directions, as it helps in determining the function's continuity and differentiability properties.
Mindmap
Keywords
💡limit
💡approaching from the left
💡function
💡table of values
💡negative superscript
💡unbounded
💡multiple choice questions
💡reasonable estimate
💡sample points
💡value of the function at a point
💡one-sided limit
Highlights
The function F is defined over the real numbers, and a table provides select values of F(x) corresponding to given x values.
The concept of limits is introduced, specifically focusing on the limit of F(x) as x approaches 1 from the left.
Clarification on the notation for approaching a value from the left, dispelling common misconceptions related to the negative superscript.
The importance of considering values from the left side only when estimating the limit as x approaches 1.
The method of examining values of x and F(x) to determine the limit as x approaches a certain point from the left.
The observation that the limit does not necessarily equal the function's value at the approaching point.
An example is given where F(x) appears to approach 2 as x gets closer to 1 from the left.
The process of estimating limits is described as providing a reasonable estimate rather than an exact value.
A second example is introduced, focusing on the limit as x approaches negative two from the left.
The explanation of how to interpret and work with negative signs in the context of approaching negative values.
The observation that the function's values are getting unbounded and increasingly negative as x approaches negative two from the left.
The conclusion that the limit as x approaches negative two from the left does not exist due to the unbounded nature.
A discussion on how to approach limits from the right and the potential difference from limits approached from the left.
An example illustrating that the limit from the right approaches negative four, which is different from the left approach.
The general principle that if the limit from the left is different from the right, the function's limit at that point does not exist.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: