BusCalc 02 Limits and Continuity
TLDRThe video script delves into the concept of one-sided and two-sided limits in calculus, illustrating how these mathematical tools help understand the behavior of functions at points of discontinuity. It explains that a one-sided limit, either left or right, is the value a function approaches as the input gets arbitrarily close to a certain point from a specific direction. The script uses examples of point, jump, essential, and oscillating discontinuities to demonstrate how limits can exist even when the function is not defined at a point. It further clarifies that a two-sided limit exists when both the left and right one-sided limits are equal and exist, which is often simply referred to as 'the limit.' The video concludes with definitions of continuity, emphasizing that a function is continuous at a point if it is defined, the two-sided limit exists and equals the function's value at that point, and the function is continuous over an interval if it is continuous at every point within that interval. The summary aims to provide a clear and concise understanding of the complex topic, making it accessible to viewers.
Takeaways
- 📌 A two-sided limit is the most common reference for 'limit' and implies both left and right limits exist and are equal.
- 📐 When a function is continuous at a point, the limit at that point is equal to the function's value at that point.
- 🔍 Limits become particularly interesting at points of discontinuity, which is where they provide meaningful information about the function's behavior.
- ➡️ A right-sided limit is denoted with a '+' sign after 'c' and is found by approaching the point from values greater than 'c'.
- ⬅️ A left-sided limit is denoted with a '-' sign after 'c' and is found by approaching the point from values less than 'c'.
- 🔁 For a point of discontinuity, even if the function is not defined at that point, it's possible to find a right-sided or left-sided limit if the function approaches a certain value.
- 🕳 At essential discontinuities, such as when the function approaches infinity or negative infinity, the limit does not exist.
- 🔄 An oscillating discontinuity results in non-existent one-sided limits due to the function's values oscillating infinitely close to the point of discontinuity.
- ⚖️ A two-sided limit exists if both the right-sided and left-sided limits exist and are equal, indicating a point of continuity.
- ⛔️ If the right-sided and left-sided limits do not agree, the two-sided limit does not exist, indicating a discontinuity at that point.
- 📈 A function is considered continuous at a point 'c' if it is defined, its two-sided limit exists, and the function value at 'c' equals the two-sided limit.
Q & A
What are the two types of one-sided limits?
-The two types of one-sided limits are left-sided limits and right-sided limits.
What is the symbolic notation for a right-sided limit?
-The symbolic notation for a right-sided limit is written as 'lim (x -> c^+) f(x)', where the plus sign indicates the right-sided approach.
How is a function's limit at a point related to its continuity at that point?
-If a function is continuous at a point, the limit of the function as x approaches that point is equal to the function evaluated at that point.
What is a jump discontinuity?
-A jump discontinuity occurs when a function has a sudden 'jump' or break in its graph at a certain point, resulting in different left-sided and right-sided limits that are not equal.
What does it mean for a function to have an essential discontinuity?
-An essential discontinuity means that the function approaches infinity as x approaches the point of discontinuity from either side.
How is a left-sided limit different from a right-sided limit in terms of notation?
-A left-sided limit is denoted with a negative sign after the constant 'c' in the limit expression, written as 'lim (x -> c^-) f(x)', indicating an approach from the left side.
When does a two-sided limit exist?
-A two-sided limit exists when both the right-sided limit and the left-sided limit exist and are equal.
What is another term for a two-sided limit?
-A two-sided limit is often simply referred to as a 'limit' in many mathematical contexts.
What are the three conditions that must be true for a function to be considered continuous at a point?
-A function is continuous at a point if: 1) the function is defined at that point, 2) the two-sided limit exists as x approaches that point, and 3) the two-sided limit is equal to the function evaluated at that point.
What is the definition of a continuous function over an interval?
-A function is continuous over an interval if it is continuous at every point within that interval.
What is the intuitive way to understand continuity in a function?
-A function is intuitively continuous if you can draw its curve on the xy-plane without lifting your pen.
Why do mathematicians define continuity so specifically?
-Mathematicians define continuity specifically to establish a clear and precise understanding of the concept, which is fundamental to calculus and analysis.
Outlines
📚 Introduction to One-Sided and Two-Sided Limits
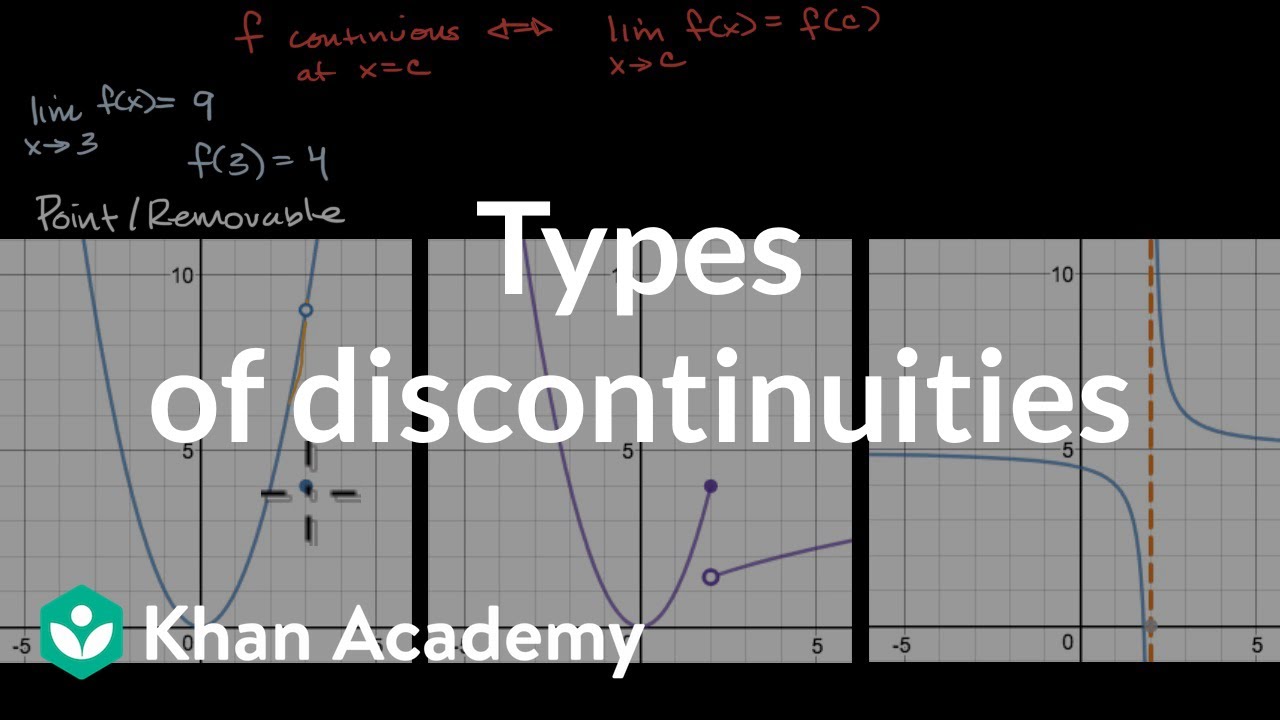
This paragraph introduces the concept of limits in calculus, differentiating between one-sided (left or right) and two-sided limits. It explains that when a function is continuous, the limit at a point is simply the value of the function at that point, using the example of a function f(x) being continuous at x=5 with f(5)=42. The paragraph also sets up the discussion for limits at points of discontinuity, which is where limits become particularly interesting. The symbolic notation for a right-sided limit is introduced, emphasizing the '+' sign following 'c' to denote approach from the right.
🔍 Evaluating Right-Sided Limits at Discontinuities
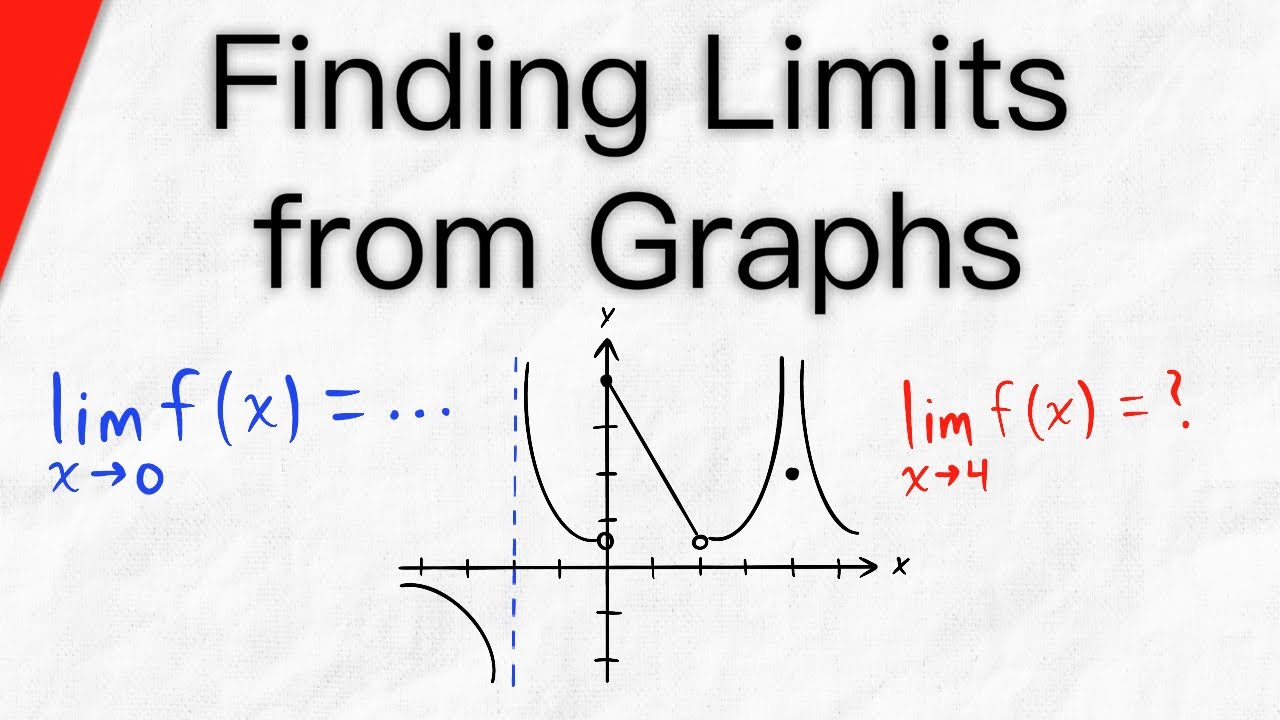
The paragraph delves into finding right-sided limits at points of discontinuity. It uses several examples, including a point discontinuity at x=-3, a jump discontinuity at x=-1, and an essential discontinuity at x=-2. In each case, the right-sided limit is found by approaching the discontinuity from values greater than the point of discontinuity. The outcomes vary: for the point discontinuity, the right-sided limit is -2; for the jump discontinuity, it's 1; and for the essential discontinuity, the function approaches positive infinity. An oscillating discontinuity at x=0 is also mentioned, where the right-sided limit does not exist due to the function's erratic behavior.
🔄 Examining Left-Sided Limits and Their Comparison
This section discusses left-sided limits, which are similar to right-sided limits but approached from the left side of the discontinuity. The notation for a left-sided limit is introduced, with a '-' sign following 'c'. The paragraph revisits the point, jump, and essential discontinuities to find their left-sided limits. For the point discontinuity, the left-sided limit is also -2, matching the right-sided limit. However, for the jump discontinuity, the left-sided limit is -1, differing from the right-sided limit. For the essential discontinuity, the left-sided limit is negative infinity, contrasting with the positive infinity of the right-sided limit. The oscillating discontinuity is noted to have a non-existent left-sided limit, similar to the right-sided limit.
🔗 Understanding Two-Sided Limits and Continuity
The concept of two-sided limits is explained as existing when both the right-sided and left-sided limits exist and are equal. The notation for a two-sided limit is presented without a '+' or '-' sign after 'c'. Examples are used to illustrate when two-sided limits exist or do not exist. For instance, at x=-3, the two-sided limit exists and is -2; at x=-1, it does not exist because the one-sided limits differ; at x=-2 for the essential discontinuity, the two-sided limit does not exist due to differing one-sided limits of positive and negative infinity; and for the oscillating discontinuity at x=0, the two-sided limit does not exist as neither one-sided limit exists. The paragraph concludes with a definition of continuity: a function is continuous at a point if it is defined, its two-sided limit exists and is equal to the function's value at that point, and this holds true for every point in the function's domain.
🌀 Continuity Over Intervals and the Entire Domain
The final paragraph expands on the concept of continuity, stating that a function is continuous over an interval if it is continuous at every point within that interval. It also defines a function as a continuous function if it is continuous over its entire domain. The paragraph reiterates the three definitions of continuity given in the course, emphasizing that they all convey the same concept. A practical way to remember continuity is by considering whether the function's curve can be drawn without lifting the pen from the paper, which would indicate a discontinuity if done so.
Mindmap
Keywords
💡One-sided limits
💡Two-sided limits
💡Continuity
💡Point discontinuity
💡Jump discontinuity
💡Essential discontinuity
💡Oscillating discontinuity
💡Left-sided limit
💡Right-sided limit
💡Domain
💡Interval
Highlights
One-sided limits can be either left-sided or right-sided, and are represented by a plus or minus sign following the approach value.
Two-sided limits are often simply referred to as 'limits' and assume both left and right sides are being considered.
For a function to be continuous at a point, the limit at that point must be equal to the function's value there.
Limits become particularly interesting when considering points of discontinuity in a function.
Discontinuities include jump, point, essential, and oscillating discontinuities, each with unique limit behaviors.
The right-sided limit is found by approaching the point from values greater than the discontinuity point.
A function with a point discontinuity may not be defined at the point, but a right-sided limit can still exist.
For jump discontinuities, the right-sided limit can be determined by approaching from the right and observing the function's approach value.
Essential discontinuities can lead to right-sided limits approaching infinity or negative infinity.
Oscillating discontinuities result in non-existent right-sided limits due to the function's unpredictable behavior near the point.
Left-sided limits are similar to right-sided limits but approach the point from values less than the discontinuity point.
For some functions, left-sided and right-sided limits at a point may be equal, indicating a two-sided limit exists.
A two-sided limit does not exist if the right-sided and left-sided limits are not equal or if one of them does not exist.
Continuity of a function at a point requires the function to be defined, the two-sided limit to exist, and the limit to equal the function's value.
A function is considered continuous over an interval if it is continuous at every point within that interval.
A function is termed a continuous function if it is continuous over its entire domain.
A practical way to remember continuity is to visualize if you can draw the function's curve without lifting your pen.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: