Newton, Leibniz, and Usain Bolt | Derivatives introduction | AP Calculus AB | Khan Academy
TLDRThe video script discusses the foundational concepts of differential calculus, emphasizing its relevance to understanding instantaneous rates of change. It draws a connection between the work of historical figures like Isaac Newton and Gottfried Leibniz and the contemporary example of Usain Bolt's sprinting speed. The script explains how traditional algebra can calculate average speed but introduces the concept of a derivative to determine instantaneous velocity, using Bolt's record-breaking sprint as a practical illustration.
Takeaways
- 🌟 Isaac Newton and Gottfried Leibniz are renowned for their independent contributions to the development of calculus.
- 🏃 Usain Bolt's achievement as a sprinter is used as an analogy to explain the concept of instantaneous rate of change in calculus.
- 📈 The fundamental question that connects Newton, Leibniz, and Bolt is understanding the instantaneous rate of change of a variable.
- 🎯 Differential calculus focuses on finding the instantaneous rates of change, which is crucial for understanding the behavior of functions at a specific point.
- 📊 The average speed of Bolt can be calculated using the traditional algebraic method of dividing the change in distance by the change in time.
- 🚀 Instantaneous speed differs from average speed as it represents the speed at a particular moment, not over a period.
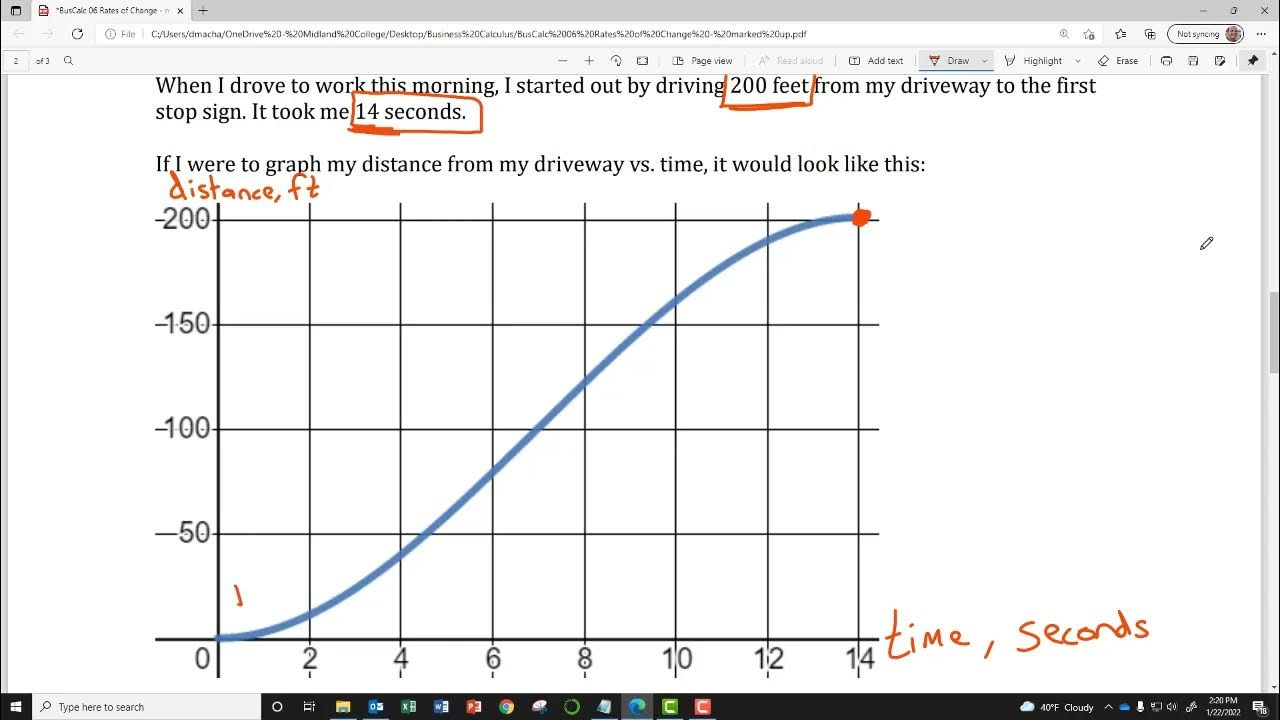
- 📉 The concept of a graph is introduced to visualize the distance traveled by Bolt against time, highlighting the difference between average and instantaneous speed.
- 🤔 The challenge of calculating instantaneous velocity lies in the continuously changing slope of the curve representing Bolt's motion.
- 🔢 The derivative, represented as dy/dx, is introduced as the mathematical term for the instantaneous slope or rate of change of a function.
- 🌐 The differential notation (dy and dx) signifies infinitesimally small changes in y and x, respectively, which are essential for determining instantaneous rates of change.
Q & A
Who are the two famous individuals mentioned at the beginning of the script and what are they known for?
-The two famous individuals mentioned at the beginning of the script are Isaac Newton, a British mathematician and physicist, and Gottfried Leibniz, a German philosopher and mathematician. They are both known as the founding fathers of calculus and did most of their major work in the late 1600s.
What is the fundamental question that both Newton and Leibniz were obsessed with, which is also addressed in differential calculus?
-The fundamental question that both Newton and Leibniz were obsessed with is 'what is the instantaneous rate of change of something?' This question is central to the study of differential calculus, which focuses on finding instantaneous rates of change.
How does the script use Usain Bolt to illustrate the concept of instantaneous rate of change?
-The script uses Usain Bolt, a Jamaican sprinter, to illustrate the concept of instantaneous rate of change by asking how fast he is going at any given moment during his run, rather than his average speed over a period of time. This highlights the difference between average speed and instantaneous speed, which is a key concept in differential calculus.
What is the method of fluxions and how is it related to differential calculus?
-The method of fluxions is the original term used by Isaac Newton for what we now call differential calculus. It refers to the study of rates of change and the calculation of instantaneous speeds or slopes at any point in a function, focusing on what is happening in an instant.
How does the script explain the difference between average speed and instantaneous speed?
-The script explains that average speed is calculated as the total change in distance divided by the total change in time, representing the overall rate of change over a period. In contrast, instantaneous speed is the speed at any specific moment, which can be found by taking the limit as the time interval approaches zero, essentially finding the slope of the tangent line at that point on the function.
What is the mathematical notation used in calculus to represent the derivative, and what does it signify?
-The mathematical notation used in calculus to represent the derivative is dy/dx. It signifies the rate of change of a function with respect to its variable, or in other words, the instantaneous slope of the function at any given point.
What is the role of differentials in the concept of instantaneous rate of change?
-Differentials, represented by dy for the infinitesimal change in y and dx for the infinitesimal change in x, are used to approximate the instantaneous rate of change. By considering infinitesimally small changes in x and the corresponding changes in y, we can better approximate the instantaneous slope or speed at a specific point.
How does the concept of limits come into play when calculating instantaneous speed?
-The concept of limits is crucial in calculating instantaneous speed as it involves taking the limit as the change in time (delta x) approaches zero. This limit gives us the instantaneous rate of change, which is the precise speed at any given moment, rather than an average over a period of time.
What is the peak instantaneous velocity of Usain Bolt mentioned in the script?
-The script mentions that Usain Bolt's peak instantaneous velocity is closer to 30 miles per hour, which is different from his average speed of approximately 23.5 miles per hour.
How does the script illustrate the concept of acceleration and deceleration in relation to instantaneous speed?
-The script illustrates the concept of acceleration and deceleration by describing Usain Bolt's speed during a race. It explains that his speed starts off slower, then accelerates, reaches a peak instantaneous velocity, and finally slows down towards the end of the race. This change in speed over time shows how the instantaneous rate of change can vary throughout a process.
What is the significance of the slope of the tangent line in the context of differential calculus?
-In the context of differential calculus, the slope of the tangent line at a particular point on a function represents the instantaneous rate of change or speed at that point. It is the derivative of the function, which gives the precise measure of change at that instant, rather than an average over a range of values.
Outlines
🌟 Introduction to Differential Calculus and Instantaneous Rate of Change
This paragraph introduces the audience to the concept of differential calculus, highlighting its historical roots with mathematicians Isaac Newton and Gottfried Leibniz. It emphasizes the importance of understanding the instantaneous rate of change, using the example of Usain Bolt's speed to illustrate the difference between average speed and instantaneous speed. The explanation progresses to discuss how traditional algebra can be limited in capturing this instantaneous change, leading to the need for calculus. The paragraph sets the stage for a deeper exploration of differential calculus, including the method of fluxions introduced by Newton, and the graphical representation of distance over time to demonstrate the concept of slope as rate of change.
🏃♂️ Usain Bolt's Speed and the Concept of Instantaneous Velocity
This paragraph delves into the specifics of calculating Usain Bolt's average speed and contrasts it with his instantaneous velocity. It explains how the average speed is calculated by dividing the total distance by the total time, and how this represents the average rate of change. The paragraph then introduces the idea of instantaneous velocity, which is the speed at any given moment, and how it differs from average speed. The discussion includes a hypothetical graphical representation of Bolt's distance relative to time, illustrating the varying slopes that represent his acceleration and deceleration. The paragraph concludes with the introduction of the concept of taking a limit as the change in time approaches zero to find the instantaneous rate of change, which is the derivative in calculus, represented as dy/dx.
Mindmap
Keywords
💡Isaac Newton
💡Gottfried Leibnitz
💡Calculus
💡Instantaneous Rate of Change
💡Usain Bolt
💡Average Speed
💡Slope
💡Derivative
💡Limit
💡Differential
💡Acceleration
Highlights
Isaac Newton and Gottfried Leibniz are recognized as the founding fathers of calculus, having done most of their major work in the late 1600s.
Both Newton and Leibniz were obsessed with understanding the instantaneous rate of change of something, a fundamental question in differential calculus.
Usain Bolt, a Jamaican sprinter, is used as an example to illustrate the concept of instantaneous rate of change in relation to his speed during a race.
The method of fluxions, originally coined by Newton, is an early term for differential calculus, focusing on what happens in a given instant.
To understand the challenge of calculating instantaneous rates of change, a graph is introduced with distance on the y-axis and time on the x-axis.
Usain Bolt's distance as a function of time is plotted, with his starting position at time zero and his capability to cover 100 meters in 9.58 seconds.
Average speed is calculated as the change in distance over the change in time, demonstrated using the slope between two points on the graph.
The concept of slope as rate of change is explained, with units of speed derived from this calculation.
Usain Bolt's average speed is calculated to be approximately 10.4 meters per second, based on his 100-meter dash time.
The difference between average speed and instantaneous speed is introduced, with an emphasis on understanding Bolt's speed at any given moment.
A potential plot of Bolt's distance relative to time is described as a curve, showing his acceleration and deceleration throughout the race.
The peak instantaneous velocity of Usain Bolt is mentioned to be closer to 30 miles per hour, different from his average speed.
The process of approximating the slope at different points on the curve is discussed to find the instantaneous rate of change.
The concept of taking the limit as the change in x approaches 0 to find the instantaneous rate of change is introduced.
The derivative is defined as the instantaneous slope at a point on the curve, represented by the calculus terminology 'dy/dx'.
The differential is explained as an infinitely small change in y over an infinitely small change in x, essential for calculating instantaneous slope.
The importance of not letting the change in x be zero is emphasized, as division by zero is undefined, and instead, the limit as it approaches 0 is taken.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: