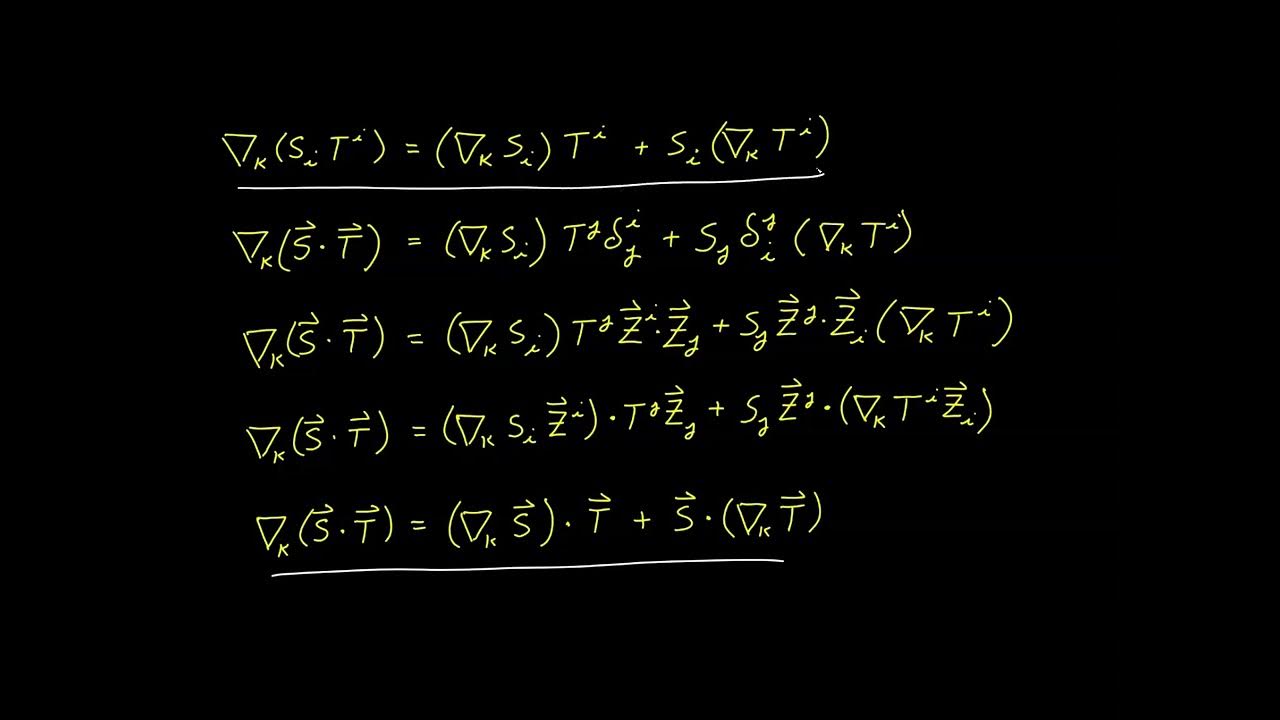What's a Tensor?
TLDRIn this informative video, Dan Fleisch introduces tensors as a broader class of objects beyond vectors, using everyday objects and simple explanations. He explains vectors as arrows with magnitude and direction, and further delves into tensor components and basis vectors within the Cartesian coordinate system. Fleisch creatively employs shadows and projections to illustrate how vector components are determined. The video progresses to describe higher-rank tensors, their representations, and applications, such as describing forces within a solid object. The key message is that tensors' power lies in their universality across different reference frames, a concept Lillian Lieber referred to as 'the facts of the universe'.
Takeaways
- 📚 Introduction to tensors is aimed to be understood without complex mathematical equations, using everyday objects.
- 🎯 Understanding of vectors is fundamental before diving into tensors, as vectors are part of a wider class of objects called tensors.
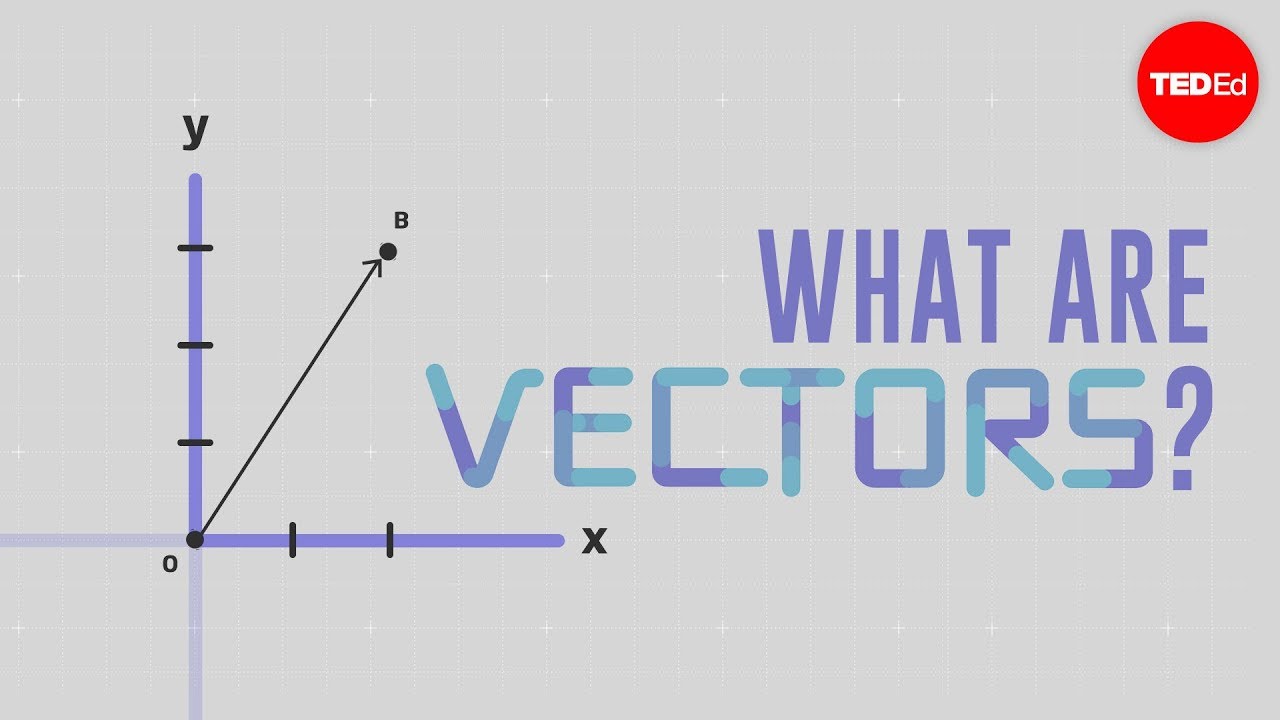
- 🔵 Vectors represent quantities with both magnitude and direction, like force, magnetic fields, or velocities.
- 📐 A vector can also represent an area, with the length proportional to the area and the direction perpendicular to the surface.
- 🌐 Coordinate systems and basis vectors (unit vectors) are essential for discussing vector components.
- 🔍 Vector components are found by projecting the vector onto the coordinate axes and can be visualized using shadows or by counting unit vectors.
- 🔢 Vector components are represented as an array or column vector with indices corresponding to the basis vectors.
- 📈 Scalars are considered tensors of rank zero because they have no directional indicators and thus require no indices.
- 🔗 Higher-rank tensors, like rank-two and rank-three tensors, involve more components and multiple indices to represent complex physical phenomena.
- 🤔 Tensors are powerful because they provide a consistent representation of physical quantities across different reference frames.
- 🌟 Lillian Lieber referred to tensors as 'the facts of the universe' due to their invariant nature under changes in reference frames.
Q & A
What is the main goal of the video?
-The main goal of the video is to explain the concept of tensors without using mathematical equations, but instead by using simple household objects and analogies.
How does the speaker suggest one should start to understand tensors?
-The speaker suggests that to understand tensors, one should first have a solid understanding of vectors, including vector components and basis vectors.
What does a vector represent?
-A vector represents a quantity that has both magnitude and direction. It can represent physical quantities like force, the Earth's magnetic field, or the velocity of a particle in a fluid, and it can also represent an area.
How are basis vectors different from other vectors?
-Basis vectors, or unit vectors, have a length of one and their direction is aligned with the coordinate axes. They are used as a reference in a coordinate system to express the components of other vectors.
How does the speaker demonstrate finding the x-component of a vector?
-The speaker demonstrates finding the x-component by projecting the vector onto the x-axis, using a lamp to cast a shadow of the vector on the axis, and measuring the shadow's length on the axis.
What is the significance of the components of a vector?
-The components of a vector are significant because they express the vector in terms of the basis vectors of a coordinate system. This allows for a more precise representation and manipulation of vectors in various applications.
Why are tensors considered powerful in physics?
-Tensors are considered powerful because they provide a framework that is invariant across different reference frames. The combination of components and basis vectors remains consistent for all observers, regardless of their reference frame.
What is a rank-two tensor and why is it used?
-A rank-two tensor is a mathematical object used to represent multi-dimensional data where each component is associated with two indices. It is used to describe more complex relationships, such as the forces acting on different surfaces within a solid object.
How does the transformation of basis vectors and components in different reference frames contribute to the consistency of tensors?
-The basis vectors transform in a specific way between reference frames, and the components transform in a manner that maintains the combination of components and basis vectors. This ensures that the tensor's representation remains consistent for all observers.
What did Lillian Lieber call tensors, and why?
-Lillian Lieber called tensors 'the facts of the universe' because of their ability to consistently represent physical quantities across different reference frames, making them fundamental to the understanding of the physical world.
How does the speaker visualize vector components?
-The speaker visualizes vector components by projecting the vector onto the coordinate axes and considering the shadows cast by the vector on these axes. Another way is by considering how many unit vectors in each direction are needed to reach from the base to the tip of the vector.
Outlines
📚 Introduction to Vectors and Tensors
The speaker, Dan Fleisch, introduces the topic of vectors and tensors, aiming to explain what a tensor is without using complex mathematical equations. He emphasizes the importance of understanding vectors first and uses everyday objects to illustrate concepts. The explanation begins with the basic definition of a vector as an arrow representing a quantity with magnitude and direction, and extends to how vectors can represent areas by making the arrow's direction perpendicular to the surface. The introduction of coordinate systems and basis vectors sets the foundation for understanding vector components and the transition to tensors.
🌟 Vector Components and Basis Vectors
This paragraph delves into the concept of vector components and basis vectors. The speaker explains how to find the x and y components of a vector by projecting it onto the respective axes, using shadows as a visual aid. He introduces the idea of representing vectors through their components in terms of basis vectors, which can be written as an array or stacked with parentheses, resembling column vectors. The explanation extends to higher-dimensional vectors, emphasizing the need for indices to denote the direction of each component. Scalars are introduced as tensors of rank zero, and the concept of rank-one tensors is established.
📈 Higher-Rank Tensors and Their Applications
The speaker discusses higher-rank tensors, specifically rank-two and rank-three tensors in three-dimensional space. He uses the example of forces inside a solid object to illustrate the need for a nine-component, two-index representation for rank-two tensors. The explanation progresses to rank-three tensors, which have 27 components and three indices, each corresponding to a different set of three basis vectors. The speaker highlights the power of tensors in maintaining their form across different reference frames, a characteristic that led to tensors being called 'the facts of the universe'.
Mindmap
Keywords
💡Tensors
💡Vectors
💡Magnitude
💡Direction
💡Basis Vectors
💡Components
💡Projection
💡Coordinate System
💡Rank
💡Transformation
💡Physical Interpretation
Highlights
Dan Fleisch introduces a new students guide on vectors and tensors.
The goal is to explain tensors without using complex mathematical equations.
Understanding tensors begins with a solid grasp of vectors.
Vectors represent quantities with both magnitude and direction.
Vectors can also represent areas, with length proportional to the area.
Vector components and basis vectors are key to understanding tensors.
The Cartesian coordinate system and its unit vectors are introduced.
Finding vector components involves projecting the vector onto axes.
Vector components can be visualized by counting unit vectors along axes.
Vectors can be represented by their components in an array or column vector.
Scalars are considered tensors of rank zero, with no directional indicators.
Rank-two tensors have nine components and nine sets of two basis vectors.
Rank-two tensors can represent forces on surfaces within a solid object.
Rank-three tensors consist of 27 components with three indices each.
Tensors' power lies in their consistency across different reference frames.
Lillian Lieber referred to tensors as 'the facts of the universe'.
The video aims to make understanding tensors accessible through simple household objects.
The explanation uses children's blocks, arrows, cardboard, and a pointed stick.
The video is designed to last about 12 minutes for a concise understanding.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: