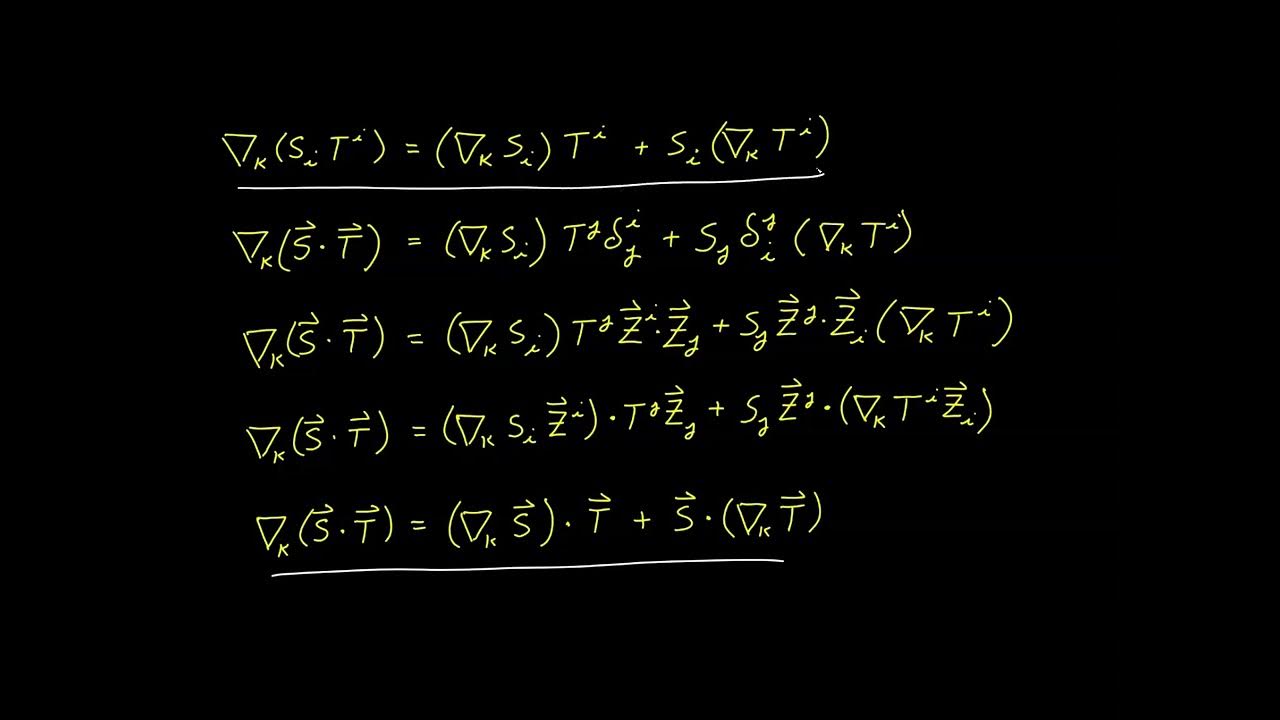Tensors for Beginners 14: Tensors are general vector/covector combinations
TLDRThe video delves into the concept of general tensors, explaining how they are constructed from combinations of vectors and covectors using the tensor product. The speaker introduces new types of tensors, explores transformation rules, multiplication formulas, and array shapes, and emphasizes the complexities involved as tensors become larger. The importance of Einstein notation for simplifying tensor operations is highlighted, particularly for high-rank tensors where array representation becomes cumbersome. Ultimately, tensors are defined as collections of vectors and covectors, with their properties and transformations determined by their basis.
Takeaways
- 📚 The video discusses generalizing the concept of the tensor product to create general tensors using combinations of vectors and covectors.
- 🔄 The script introduces a non-standard tensor product notation, different from the circle-times symbol typically found in textbooks.
- 🗺 Linear maps are explained as linear combinations of vector-covector pairs, which simplifies understanding transformation rules, multiplication formulas, and array shapes.
- 📈 Bilinear forms are also described as linear combinations of covector-covector pairs, following a similar pattern to linear maps for ease of understanding.
- 🆕 The video introduces new tensors, 'D' and 'Q', with 'D' being a (2,0)-tensor made of vector pairs and 'Q' a (1,2)-tensor with one vector and two covector parts.
- ❓ It's highlighted that there isn't a single way for tensor 'Q' to act on tensor 'D', emphasizing the complexity of higher-dimensional tensors.
- 🔧 The transformation rules for tensors are simplified by using linear combinations and the transformation rules for basis vectors and covectors.
- 🧩 The script explains that tensor components can be visualized as arrays, similar to the Kronecker product, which helps in understanding their shapes and multiplication.
- 📉 For high type tensors, the array representation becomes less useful due to the multiple possible multiplication rules, making Einstein notation more preferable.
- 📝 The importance of basis choice in tensor representation is emphasized, noting that different bases can yield different components for the same tensor.
- 🔑 The script concludes by defining tensors as collections of vectors and covectors combined using the tensor product, and the importance of understanding transformation rules and Einstein notation for complex tensors.
Q & A
What is the main topic of the video?
-The video discusses the generalization of tensor products to general tensors, which can be made using any combination of vectors and covectors.
What is the significance of the tensor product in the context of tensors?
-The tensor product is crucial for combining vectors and covectors to create tensors of various types, which are then used to define linear maps, bilinear forms, and more complex tensors.
How are linear maps related to tensors?
-Linear maps can be understood as linear combinations of vector-covector pairs, and this perspective helps in deriving transformation rules, multiplication formulas, and array shapes for tensors.
What is a (2,0)-tensor and how is it constructed?
-A (2,0)-tensor, like tensor D mentioned in the video, is constructed from pairs of vectors, indicating it has two contravariant parts and no covariant parts.
What are the transformation rules for tensors?
-Transformation rules for tensors involve applying the transformation rules for basis vectors and covectors. For example, a (2,0)-tensor would require applying the vector basis transformation twice.
Why is the multiplication of larger tensors, like Q and D, ambiguous?
-The multiplication of larger tensors is ambiguous because there are multiple ways to pass input vectors to covectors, leading to different possible results for the same tensor product.
What is the advantage of using Einstein notation for tensor multiplication?
-Einstein notation simplifies tensor multiplication by making the summation rules explicit, which is especially useful for high-type tensors where multiple multiplication paths exist.
How can tensor arrays be visualized, and what are the limitations of this visualization?
-Tensor arrays can be visualized as a Kronecker product of vectors and covectors, resulting in structures like 'columns of columns' or 'rows of rows of columns.' However, visualizing tensors this way can obscure important information about their covariant and contravariant parts.
Why might array notation be less useful for high-type tensors?
-Array notation might be less useful for high-type tensors because the multiple possible multiplication rules make it difficult to perform straightforward array multiplication without ambiguity.
What is the best definition of tensors according to the video?
-Tensors are best defined as collections of vectors and covectors combined using the tensor product, and their transformation rules can always be determined based on this combination.
Outlines
🔢 Generalizing Tensors and Transformation Rules
This paragraph introduces the concept of general tensors, building on the previous understanding of tensor products. It discusses the generalization to tensors that can be formed using various combinations of vectors and covectors. The explanation highlights the importance of understanding transformation rules, multiplication formulas, and array shapes for these tensors. The speaker introduces new tensors D (a (2,0)-tensor) and Q (a (1,2)-tensor) and emphasizes the ease of determining transformation rules by expressing tensors as linear combinations of basis vectors and covectors.
🧠 Understanding Tensor Multiplication Ambiguities
This section delves into the complexities of tensor multiplication, particularly when dealing with higher-order tensors like Q and D. Unlike simpler cases where the multiplication is straightforward, the speaker explains that multiple valid methods exist to apply one tensor to another. The example of linear maps versus the tensors Q and D highlights how the number of vectors and covectors introduces multiple possible summation rules, leading to different results. The discussion underscores the ambiguity and the need for careful notation, such as Einstein notation, to specify operations clearly.
📏 Exploring Array Shapes of Tensors
This paragraph examines the array shapes that result from tensor products, using specific examples to illustrate the point. The speaker compares tensor products to Kronecker products of vectors, showing how the shape of the resulting arrays can be visualized. The speaker demonstrates this with the tensors D and Q, noting that while some might prefer visualizing tensors as 3D cubes, it can obscure important information about the tensor's structure. Instead, they advocate for a row of rows of columns approach to maintain clarity on the tensor's type and its vector-covector parts.
🛠️ Practical Challenges of High-Order Tensors
This final paragraph addresses the practical difficulties of working with high-order tensors, especially when it comes to array representations and tensor multiplication. The speaker explains that while array notation is useful for low-order tensors, it becomes less effective for higher-order tensors like Q and D, where multiple valid multiplication rules exist. As a result, the speaker suggests using Einstein component notation to express multiplication rules more clearly. The discussion concludes by emphasizing the importance of remembering that tensor components depend on the chosen basis and can vary with different bases.
Mindmap
Keywords
💡Tensor
💡Covector
💡Transformation Rules
💡Bilinear Form
💡Kronecker Product
💡Einstein Notation
💡Linear Map
💡Array Shape
💡Contravariant and Covariant Parts
💡Tensor Multiplication
Highlights
Introduction to general tensors made from any combination of vectors and covectors.
Use of non-standard tensor product notation without the circle-times symbol.
Linear maps as linear combinations of vector-covector pairs for deriving transformation rules and multiplication formulas.
Bilinear forms as linear combinations of covector-covector pairs with easy derivation of properties.
Introduction of new tensors D (2,0) and Q (1,2) with unique combinations of vector and covector parts.
Exploration of coordinate transformation rules for tensors using basis vectors and covectors.
Multiplication formula for Q acting on D with multiple possible outcomes due to tensor complexity.
Discussion on the ambiguity of tensor action without specifying summation indices in Einstein notation.
Array shapes for tensors D and Q derived from Kronecker products of vectors and covectors.
Comparison of visualizing tensor arrays as 3D cubes versus rows of rows of columns for clarity.
Mechanical way of component multiplication using standard row-column multiplication rules for simpler tensors.
Limitations of array representation for high type tensors and the preference for Einstein notation.
Abstract notation for tensors as collections of vectors and covectors using tensor products.
Tensor components always come from a choice of basis and can vary with different basis representations.
Importance of understanding tensor transformation rules for both known and new tensors like D and Q.
Practical applications of Einstein component notation for clarity in tensor multiplication formulas.
Simplification of tensor representation focusing on components without basis vectors and covectors.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: