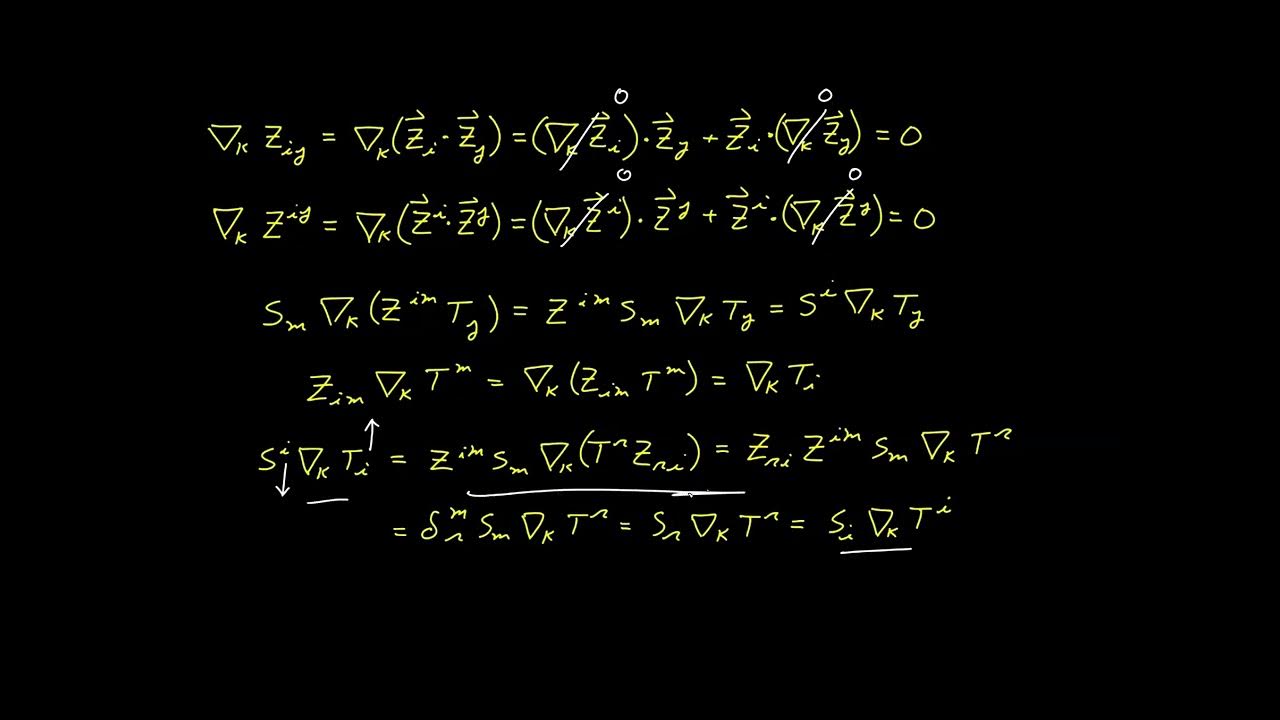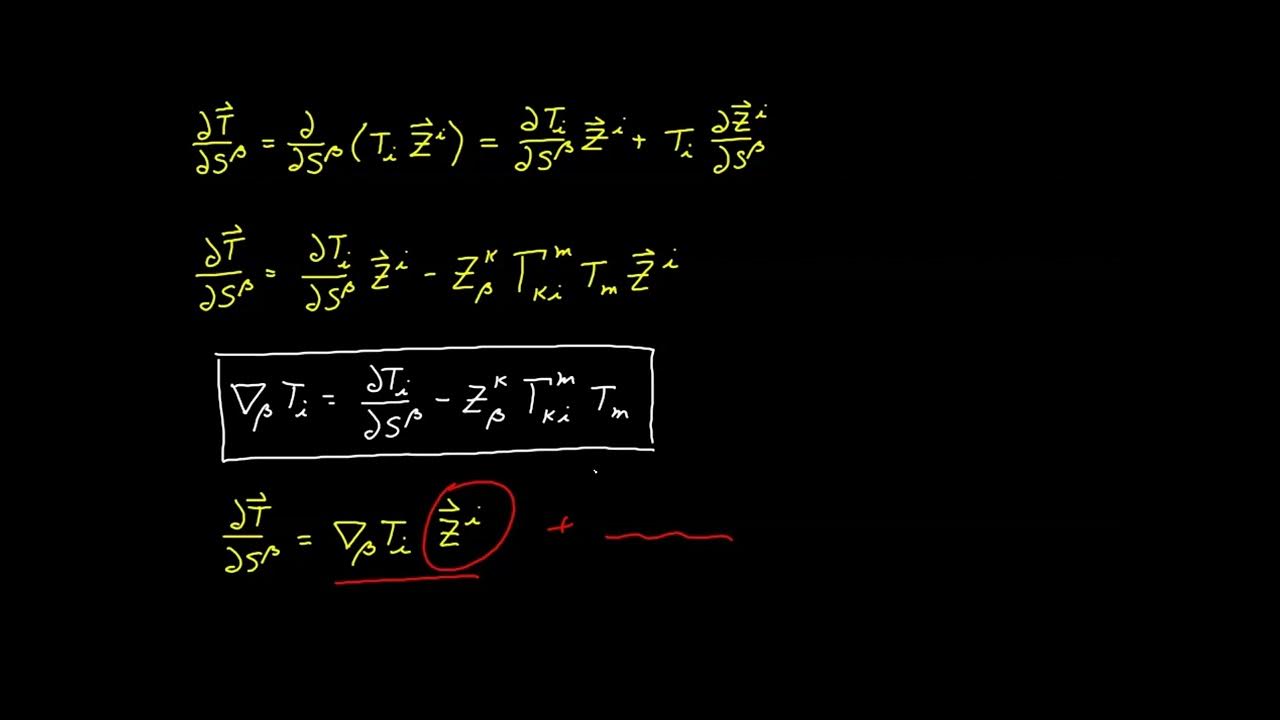Video 37 - Metrinilic Property - Part 1
TLDRThis video, part of a series on tensor calculus, delves into the covariant derivative's unique metric property. It introduces the concept of second-rank tensors represented with vector components and demonstrates how covariant derivatives operate on these tensors similarly to scalar components. The video highlights the metric property where the covariant derivative of basis vectors equals zero, simplifying the product rule in tensor calculus. Practical applications are shown, such as simplifying the covariant derivative of a dot product, making it analogous to Cartesian coordinates where basis vectors act as constants.
Takeaways
- 📚 The video is part of a series on tensor calculus, focusing on the covariant derivative and its unique properties.
- 🔍 The covariant derivative shares several properties with the partial derivative, but the video introduces the metric property, which is unique to it.
- 📈 The covariant derivative acts on scalar components of vectors, represented either in covariant or contravariant form.
- 📝 New objects with upper and lower indices are introduced, representing vectors and allowing for the representation of second-rank tensors in two different ways.
- 🧠 The concept of decomposing vectors into their individual components is extended to second-rank tensors, emphasizing the equivalence of different representations.
- 🔄 The covariant derivative can operate on tensors with vector components in the same way it operates on scalar components.
- 📚 A proof in a previous video (#33) demonstrates that the covariant derivative always produces a tensor, which applies to both scalar and vector components.
- 🎯 The basis vectors, which are second-rank tensors with vector components, have a covariant derivative equal to zero, a property known as the metric property.
- 🛠 The metric property simplifies calculations involving the covariant derivative of products, as the basis vector acts like a constant in these operations.
- 📉 The covariant derivative of a dot product can be expressed in different forms, with the metric property allowing for simplification similar to Cartesian coordinates.
- 🔗 The video concludes with a preview of further exploration of the metric property in the next video, indicating an ongoing series.
Q & A
What is the main focus of this video in the series on tensor calculus?
-The main focus of this video is to introduce the metric property, which is unique to the covariant derivative, and to explore its implications in tensor calculus.
What is the covariant derivative?
-The covariant derivative is an operation that acts directly upon the scalar component of a vector, represented either as a contravariant component or a covariant component, and it generalizes the concept of a derivative to curved spaces.
What is a second-rank tensor and how can it be represented?
-A second-rank tensor is a mathematical object that can be represented in two different ways using vector components: either as a set of three vectors with covariant indices or as a set of three vectors with contravariant indices.
What is the significance of the covariant basis vector Z in the context of this video?
-The covariant basis vector Z is significant because it is a vector with a free index and is actually a second-rank tensor with vector components, which is a concept that is further explored in the video.
What is the metric property of the covariant derivative?
-The metric property, also known as the metric compatibility, states that the covariant derivative of the metric tensor is zero, which means that the metric tensor is invariant under parallel transport.
Why is the covariant derivative of the basis vector equal to zero?
-The covariant derivative of the basis vector is equal to zero due to the metric property, which implies that the basis vectors do not change under covariant differentiation, essentially acting like constants in this context.
How does the metric property simplify the covariant derivative of a product of terms?
-The metric property simplifies the covariant derivative of a product of terms by eliminating the term that involves the covariant derivative of the basis vector, since it is zero, thus allowing the basis vector to be treated as a constant.
What is the practical application of the metric property in tensor calculus?
-The practical application of the metric property is evident when taking the covariant derivative of a dot product or a linear combination of terms, where the property allows for simplification of expressions and easier computation.
How does the covariant derivative of a dot product relate to the ordinary product rule?
-The covariant derivative of a dot product follows a similar rule to the ordinary product rule, where the covariant derivative can be distributed over the components of the dot product, thanks to the metric property.
What is the conclusion of the video regarding the covariant derivative and the metric property?
-The conclusion of the video is that the covariant derivative, due to the metric property, behaves as if the basis vectors are constants, simplifying calculations and allowing for easier manipulation of tensor expressions.
Outlines
📚 Introduction to the Metric Property in Tensor Calculus
This paragraph introduces the concept of the metric property, which is unique to the covariant derivative and is the focus of the current and next video. It revisits the expressions for the covariant derivative and explains how it acts on scalar components of vectors represented in both covariant and contravariant forms. The paragraph also introduces new objects with upper and lower indices, representing vectors and how they can be decomposed into their components using either covariant or contravariant basis vectors. The main point is that these components carry the same information as the original vectors, and different sets of scalar components can represent the same tensor.
🔍 Exploring Tensors with Vector Components and the Covariant Derivative
The second paragraph delves deeper into the concept of tensors with vector components, explaining how the covariant derivative can operate on these new objects in the same way it operates on scalar components. It references a previous video for a proof that the covariant derivative always produces a tensor and shows that basis vectors, which are second rank tensors with vector components, have been encountered before in the form of the covariant metric tensor. The covariant derivative of the basis vectors is calculated and found to be zero, which is a key part of the metric property.
📘 The Metric Property and Its Practical Applications
This paragraph discusses the practical applications of the metric property, which states that the covariant derivative of the basis vectors is zero. It illustrates how this property simplifies the calculation of the covariant derivative of a product involving basis vectors, effectively treating the basis vectors as constants in such operations. The paragraph also demonstrates the use of the metric property in the context of dot products, showing that the covariant derivative of a dot product can be calculated using a simplified form, similar to how partial derivatives are taken in Cartesian coordinates.
🔄 The Metronic Property and Its Implications for Dot Products
The final paragraph further explores the implications of the metric property for dot products. It shows how the covariant derivative of a fully contracted product can be simplified by using the dot product of basis vectors and the metric property to move the covariant basis vector inside the covariant derivative. The paragraph concludes by highlighting the equivalence of different forms for calculating the covariant derivative of a dot product, emphasizing the flexibility and utility of the metric property in tensor calculus.
Mindmap
Keywords
💡Covariant Derivative
💡Metric Property
💡Tensor
💡Contravariant and Covariant Components
💡Basis Vectors
💡Christoffel Symbols
💡Second-Rank Tensor
💡Free Index
💡Dot Product
💡Product Rule
Highlights
Introduction of the metronic property unique to the covariant derivative.
Explanation of how the covariant derivative acts on scalar components and vector components of tensors.
Introduction of new objects with upper and lower indices representing vectors to explore tensor calculus further.
Decomposition of vectors into their individual components using both covariant and contravariant basis vectors.
Representation of second-rank tensors in two different forms, emphasizing their equivalence in information content.
Demonstration that the covariant derivative operates on tensors with vector components in the same way as on scalar components.
Proof that the covariant derivative of basis vectors equals zero, known as the metronic property.
Practical application of the metronic property in simplifying the covariant derivative of a product of terms.
Illustration of how the covariant derivative 'kills the basis vector', simplifying operations as if the basis vector were constant.
Application of the metronic property to the covariant derivative of a dot product, showing its equivalence to other forms.
Discussion on the practical implications of the metronic property in tensor calculus operations.
Revisiting the product rule for dot products and its application to covariant derivatives.
Explanation of how the metronic property allows for the simplification of covariant derivatives in tensor calculus.
Connection between the metronic property and the behavior of basis vectors in covariant derivative operations.
Reinforcement of the metronic property's role in restoring constant-like behavior to basis vectors under covariant derivatives.
Preview of further exploration of the metronic property in the next video.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: