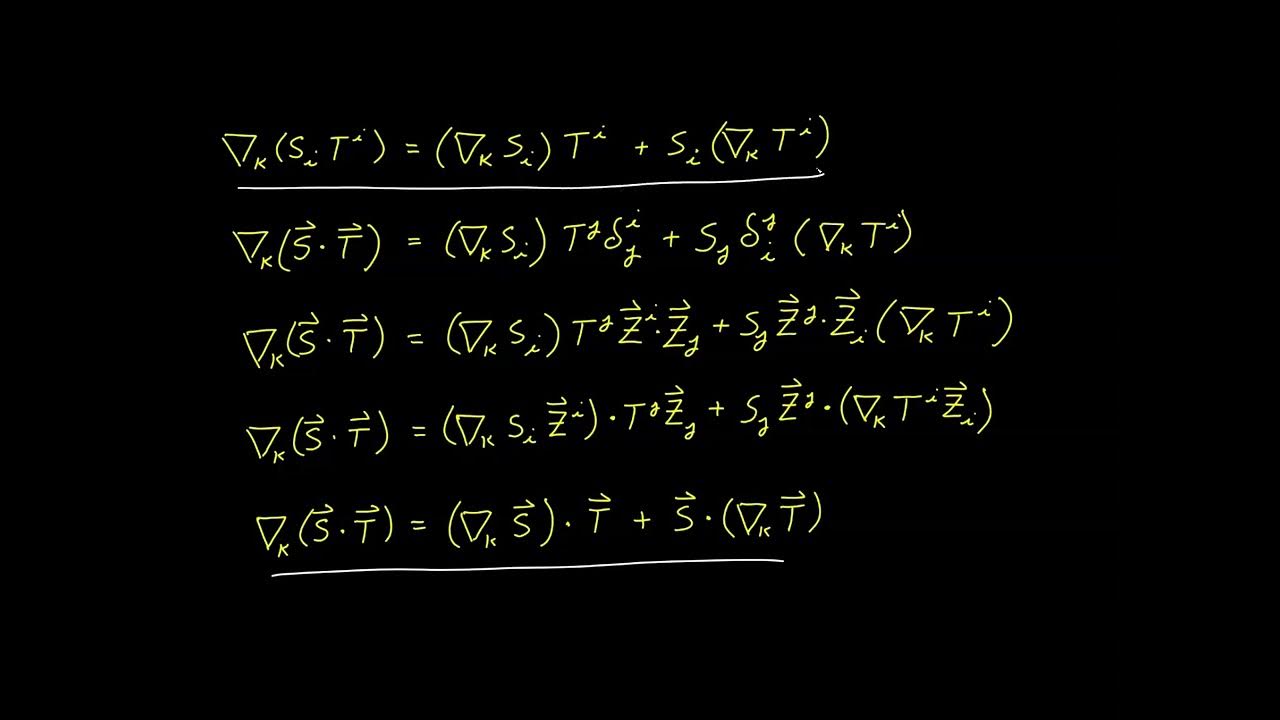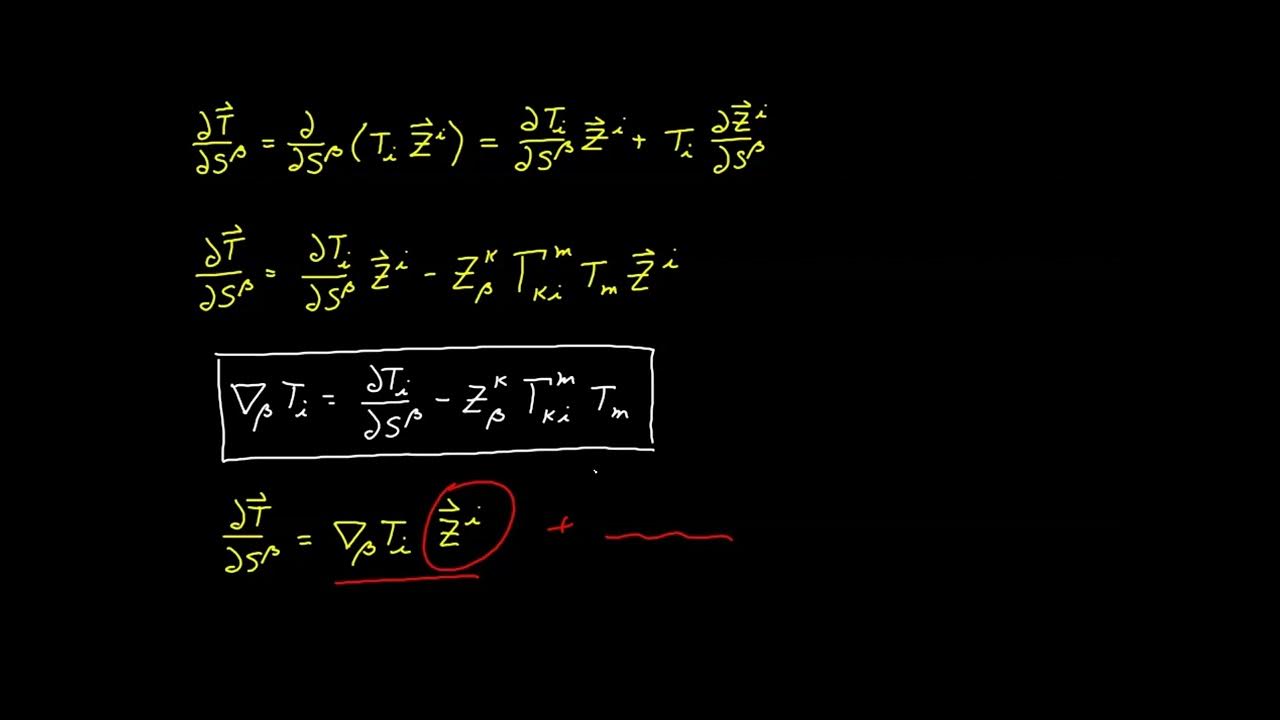Contravariant and Covariant Vectors | 1/2
TLDRThis video delves into the concepts of contravariant and covariant tensors, focusing on rank one tensors, specifically vectors. It emphasizes the invariance of tensors under coordinate transformations, contrasting with the varying components and basis vectors. Contravariant vectors are introduced as those whose components transform oppositely to the basis vectors, while covariant vectors are defined by parallel and perpendicular projections. The script uses illustrative examples to clarify these concepts, aiming to provide a foundational understanding before exploring higher rank tensors in subsequent videos.
Takeaways
- 📚 The video discusses the concepts of contravariant and covariant tensors, specifically focusing on rank one tensors, which are vectors.
- 🔗 It's recommended to review the second video in the series on tensor calculus for better understanding of the content presented in this video.
- 📍 The video uses the example of a displacement vector from JFK Airport to the Empire State Building to illustrate tensor invariance under coordinate transformations.
- 🧭 Despite changes in components and basis vectors when switching coordinate systems, the vector itself remains unchanged, which is the defining property of a tensor.
- 🔄 Vector components can change in two ways under a coordinate transformation: contravariantly or covariantly.
- 🔺 Contravariant vectors have components that change oppositely to the basis vectors under coordinate transformations.
- 🔻 Covariant vectors, on the other hand, have components that change in the same manner as the basis vectors under transformations.
- 📏 Contravariant components are specified with superscripts to indicate their opposite behavior compared to basis vectors.
- ✍️ Covariant components are denoted with subscripts, signifying their similar behavior to the basis vectors during transformations.
- 📉 The video provides an example of a 2D coordinate system with slanted axes to illustrate the meaning of contravariant components.
- 📈 It also explains covariant components by taking the dot product of a vector with basis vectors, emphasizing their transformation behavior.
- 🚫 The script mentions that covector representation and dual vectors are not the main focus of the series but are available upon request from the audience.
Q & A
What is the main topic of the video?
-The main topic of the video is contravariant and covariant tensors, specifically focusing on tensors of rank one, which are vectors.
What is recommended before watching this video?
-It is highly recommended to review the second video in the series on tensor calculus, as it provides essential understanding for the content presented in this video.
What is an example used in the video to explain the concept of a tensor?
-The video uses the displacement vector from JFK Airport in New York to the top of the Empire State Building as an example to explain the concept of a tensor.
How does the displacement vector change when switching between coordinate systems?
-The displacement vector itself does not change under a change of coordinate systems; however, its components and the basis vectors do change.
What are the two ways in which vector components can change under a coordinate transformation?
-Vector components can change either in a contravariant fashion or in a covariant fashion under a coordinate transformation.
What is the difference between a contravariant vector and a covariant vector?
-A contravariant vector has components that transform in a manner opposite to the basis vector, while a covariant vector's components transform in the same way as the basis vector.
Why are contravariant components specified with superscripts?
-Contravariant components are specified with superscripts to signify that they transform in an opposite manner to the basis vectors, which are generally specified with subscripts.
How are covariant components related to the basis vectors?
-Covariant components transform in the same way as the basis vectors under a change of coordinate systems, which is why they are specified with subscripts, similar to basis vectors.
What is the purpose of the example with the 2D coordinate system and the vector 'a' in the video?
-The example with the 2D coordinate system and the vector 'a' is used to illustrate the meaning of contravariant components and how they transform oppositely to the basis vectors.
What is the difference between a regular vector and a covector (Co-vector)?
-A regular vector is typically written as a column vector and uses contravariant components, while a covector is written as a row vector and is specified with covariant components, which are often thought of as functions rather than arrows in real space.
What are dual vectors and why are they not discussed in the video?
-Dual vectors are a concept related to covector components and are usually used as the basis for covector specification. They are not discussed in the video because they are not a high priority for tensor calculus, but the video creator is open to making videos on them if there is interest.
Outlines
📚 Introduction to Contravariant and Covariant Tensors
This paragraph introduces the topic of the video, which is the concept of contravariant and covariant tensors, specifically focusing on tensors of rank one, or vectors. The speaker emphasizes the importance of reviewing the second video in the series on tensor calculus for a foundational understanding. The paragraph uses the example of a displacement vector from JFK Airport to the Empire State Building to illustrate how vectors remain invariant under coordinate transformations, while their components and basis vectors change. The speaker clarifies the difference between contravariant and covariant vectors, explaining that these terms refer to how the components of a vector transform under a change of coordinates, not the vector itself.
🔍 Contravariant Components and Their Transformation
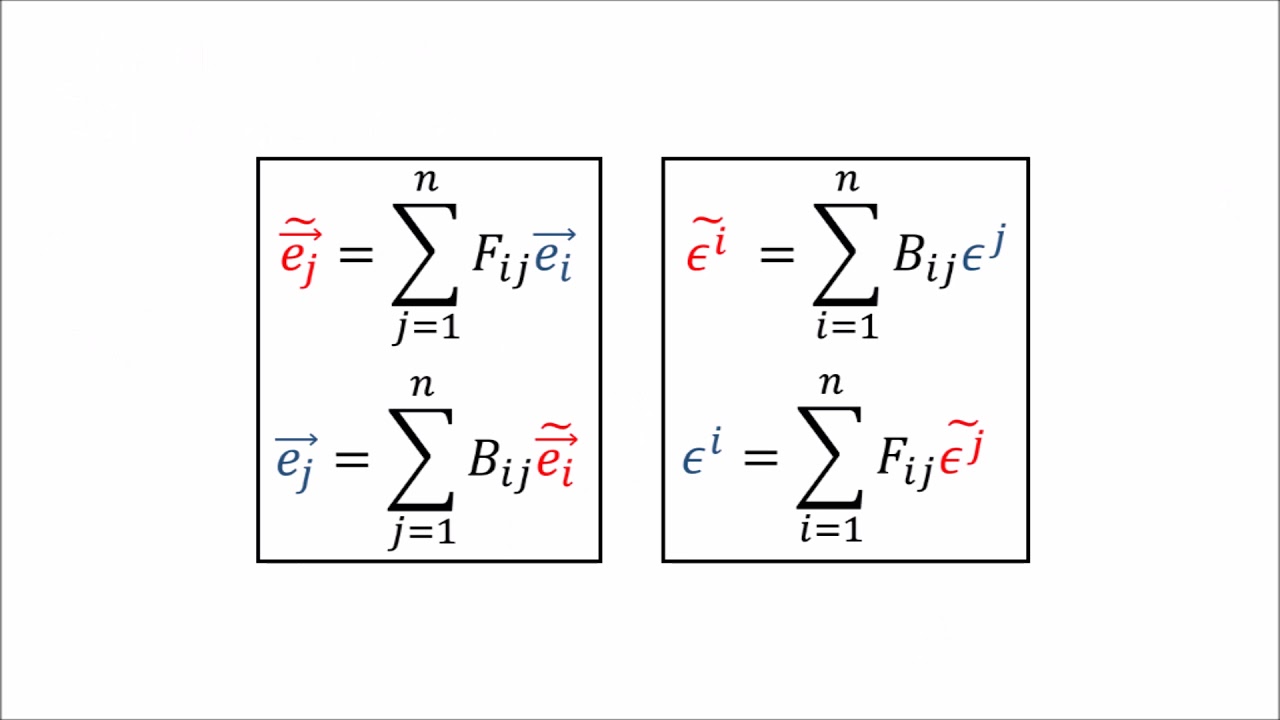
The second paragraph delves into the specifics of contravariant components, using a 2D coordinate system with slanted axes as an example. It explains how a vector can be specified by the number of basis vectors needed to construct it, and how these components change when the magnitude of the basis vectors changes. The paragraph illustrates that contravariant components transform in the opposite manner to the basis vectors, hence the use of superscripts. The example demonstrates that when the basis vector's magnitude is doubled, the corresponding contravariant component is halved, maintaining the vector's representation under the coordinate transformation.
📐 Covariant Components and Their Coordinate System Behavior
This paragraph explores covariant components, contrasting them with contravariant components by using perpendicular projections instead of parallel ones. It explains the process of defining a covariant vector through dot products with the basis vectors, resulting in scalar components that transform in the same way as the basis vectors under coordinate changes. The speaker provides an example of how covariant components behave when the coordinate system is transformed, showing that the covariant components scale with the basis vectors, hence the use of subscripts. The paragraph also addresses some caveats regarding covariant vectors, such as their representation as row vectors and their conceptualization as functions rather than arrows in space, and the use of dual vectors as the basis for covariant vectors.
🎬 Conclusion and Acknowledgment
The final paragraph wraps up the lecture by acknowledging the support of patrons and inviting viewers to engage with the content through likes and subscriptions. The speaker, Faculty of Khan, signs off, indicating the end of the video. This paragraph serves as a closing note, summarizing the video's content and encouraging viewer interaction, while also hinting at the possibility of future videos on dual vectors or covector calculus if there is sufficient interest from the audience.
Mindmap
Keywords
💡Contravariant Tensors
💡Covariant Tensors
💡Tensor
💡Vector
💡Coordinate Transformation
💡Basis Vectors
💡Displacement Vector
💡Contravariant Vector
💡Covariant Vector
💡Dot Product
💡Superscripts and Subscripts
Highlights
The video discusses the concept of contravariant and covariant tensors, specifically focusing on rank one tensors, which are vectors.
It is recommended to review the second video in the tensor calculus series for better understanding of the content presented.
The video uses a displacement vector example from JFK Airport to the Empire State Building to illustrate tensor transformation.
Tensors are invariant under a change of coordinate systems, meaning their magnitude and direction remain the same despite changes in components and basis vectors.
Vector components can change in two ways under coordinate transformation: contravariant or covariant fashion.
A contravariant vector's components transform oppositely to the basis vectors, and it is denoted with superscripts.
A covariant vector's components transform in the same manner as the basis vectors, using subscripts for representation.
The video explains the transformation of contravariant components using a 2D slanted coordinate system example.
Doubling the magnitude of a basis vector results in halving the corresponding contravariant component.
Covariant components are defined as perpendicular projections of a vector onto the coordinate axes, calculated using dot products.
The transformation of covariant components is illustrated by showing how they double when the basis vector's magnitude is doubled.
Caveats are discussed regarding the use of contravariant and covariant representations, highlighting the differences between regular vectors and covector representations.
Covector components are usually thought of as functions and specified with dual vectors, which is not the focus of this video.
The video clarifies that covector components and basis vectors behave similarly under coordinate transformations.
The upcoming video will cover more rigorous definitions of contravariant and covariant components.
The video concludes with acknowledgments to patrons and an invitation for viewers to like, subscribe, and support the channel.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: