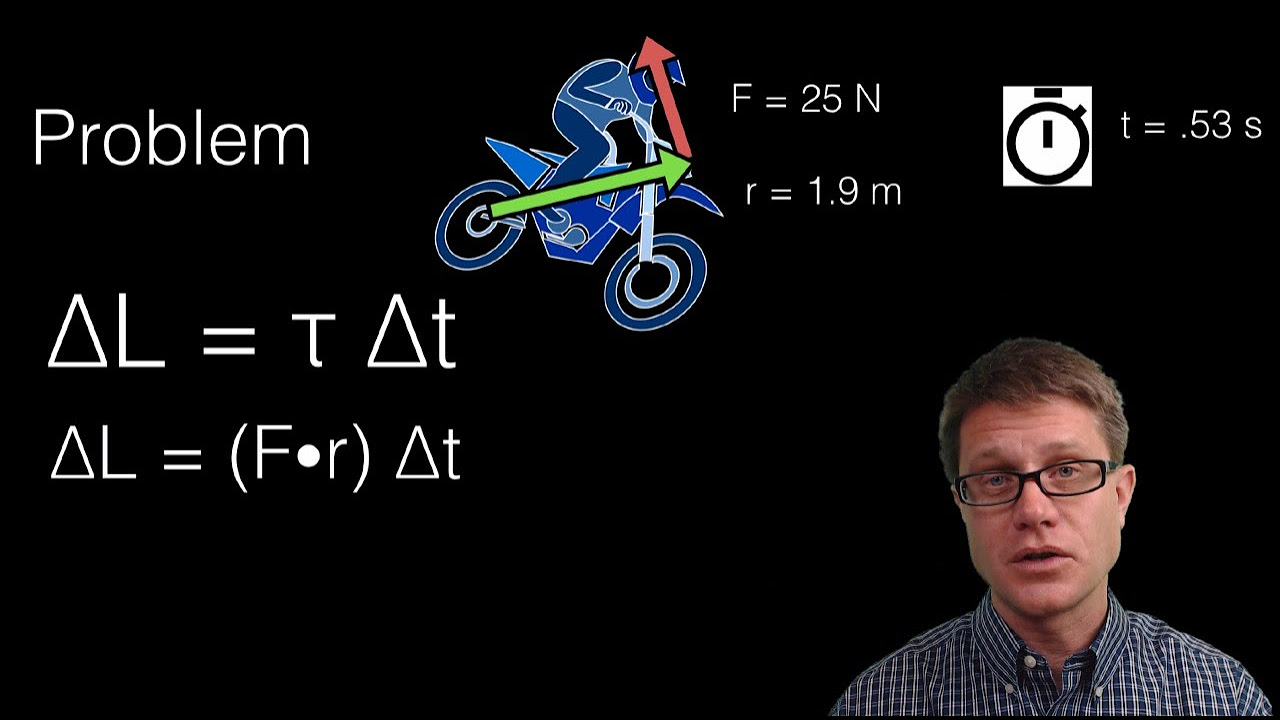The Vector Properties of Angular Quantities
TLDRIn this AP Physics essentials video, Mr. Andersen explores the vector properties of angular quantities in rotating systems, using the North Star as an analogy to explain concepts like torque, angular velocity, acceleration, and momentum. He demonstrates how these vectors can be determined using the right-hand rule and applies these principles to the behavior of a gyroscope, showing how it resists changes due to gravity and eventually precesses. The video encourages hands-on inquiry with rotating systems to better understand these physical concepts.
Takeaways
- 🌟 Understanding rotating systems and their vector properties is crucial for grasping the behavior of devices like gyroscopes.
- 📍 Angular quantities in rotating systems act as vectors, and their directions can be determined using the right-hand rule.
- 🌌 The North Star (Polaris) serves as a useful analogy for fixed points in a rotating system, as it remains constant while other stars appear to move around it.
- 🔄 All parts of a rotating system move except for the central axis, which remains stationary and is key for analyzing vector forces and accelerations.
- 💫 Torque, angular velocity, angular acceleration, and angular momentum are all vector quantities associated with rotating systems.
- 👆 The right-hand rule helps in determining the direction of these vectors: curl fingers in the direction of rotation, and the thumb points in the direction of the vector.
- 🛸 A non-rotating gyroscope will fall over due to the torque exerted by gravity, as there is no angular momentum to resist it.
- 🎯 When a gyroscope is spinning, its angular momentum resists changes due to gravity, allowing it to maintain an upright position even on a small surface like a cup.
- 🌀 Precession occurs when the gyroscope experiences a torque due to gravity, causing it to turn in a direction perpendicular to the applied torque.
- 🚴 Experimenting with larger rotating systems like bicycle wheels can provide a more tangible experience of the forces and torques involved in rotation.
- 📈 Collecting data on torque, angular velocity, angular acceleration, and momentum can be a valuable educational exercise to further understand rotating systems.
Q & A
What are the main vector properties of angular quantities discussed in the video?
-The main vector properties of angular quantities discussed are torque, angular velocity, angular acceleration, and angular momentum.
How does the analogy of the North Star help in understanding rotating systems?
-The North Star is used as an analogy to explain that in a rotating system, all parts are moving except for the central axis, similar to how the North Star appears stationary because it aligns with Earth's axis of rotation.
What is the significance of the right-hand rule in determining the direction of vector properties in rotating systems?
-The right-hand rule is significant as it provides a simple method to determine the direction of vector properties such as torque, angular velocity, angular acceleration, and angular momentum in rotating systems.
What happens to a gyroscope when it is not spinning and released?
-When a gyroscope is not spinning and released, it will simply fall over due to the torque or force exerted by gravity.
How does a spinning gyroscope resist the torque due to gravity?
-A spinning gyroscope resists the torque due to gravity because of its angular momentum, which provides resistance to changes in its state of motion.
What is the relationship between torque and the axis of rotation in a rotating system?
-Torque is the application of a force that is perpendicular to the radius of the axis of rotation, causing the object to rotate around that axis.
How does angular velocity relate to the direction of rotation?
-Angular velocity is the rate at which an object rotates around an axis, and its direction is perpendicular to the plane of rotation, pointing in the direction of the right-hand rule when applied correctly.
What is the effect of increasing angular velocity on angular acceleration?
-Increasing angular velocity results in angular acceleration, which is the rate of change of angular velocity, indicating that the object is speeding up in its rotation.
How does the force of gravity influence the precession of a gyroscope?
-The force of gravity creates a torque that is perpendicular to the axis of the gyroscope, causing it to precess or turn in a direction opposite to the force, as a result of the combined vectors of angular momentum and gravitational torque.
What can be observed when a gyroscope slows down?
-As a gyroscope slows down, it loses angular momentum, and the force of gravity becomes more dominant, eventually causing the gyroscope to fall or topple over.
What practical applications or experiments can be done to study rotating systems?
-Practical applications include using a spinning bicycle wheel or a gyroscope to observe and feel the effects of torque, angular velocity, and angular momentum. Collecting data on these quantities can help in understanding the physics of rotating systems.
Outlines
🌟 Introduction to Vector Properties of Angular Quantities
This paragraph introduces the concept of vector properties in angular quantities, focusing on rotating systems like gyroscopes. Mr. Andersen explains the importance of understanding these properties to grasp how gyroscopes maintain their orientation. The analogy of the North Star and its stationary position amidst the rotating Earth is used to illustrate the concept of a fixed axis in a rotating system. The paragraph outlines the vector nature of torque, angular velocity, angular acceleration, and angular momentum, and how they can be determined using the right-hand rule. It also touches on the behavior of a gyroscope when spinning and how it resists the torque due to gravity due to its angular momentum.
💫 Exploring Gyroscope Dynamics and Precession
In this paragraph, Mr. Andersen delves deeper into the dynamics of a spinning gyroscope, discussing the location of torque and angular momentum when the gyroscope is spinning. He explains the phenomenon of precession, which occurs due to the interplay between the gyroscope's angular momentum and the gravitational force acting perpendicular to the axis of rotation. The right-hand rule is again used to determine the direction of these vectors. The paragraph also discusses the eventual loss of angular momentum and the gyroscope's eventual fall due to the increasing torque from gravity. Practical suggestions for exploring these concepts through experiments with a gyroscope or a bicycle wheel are provided, along with a prompt for the viewer to consider how to represent and analyze the forces on a rotating system and to collect data on torque, angular velocity, acceleration, and momentum.
Mindmap
Keywords
💡Vector properties
💡Angular quantities
💡Rotating systems
💡Gyroscope
💡Torque
💡Angular velocity
💡Angular acceleration
💡Rotational inertia
💡Angular momentum
💡Precession
💡Right-hand rule
Highlights
Understanding the properties of rotating systems and their vector behavior is crucial for grasping the functioning of devices like gyroscopes.
Rotating systems, such as gyroscopes, exhibit properties that act as vectors in different directions, which can be confusing.
The North Star serves as a useful analogy for understanding rotating systems, as it remains stationary while other stars appear to move around it due to Earth's rotation.
In a rotating system, all parts are in motion except for the central axis, which remains fixed and is key to determining vector forces and accelerations.
The right-hand rule is a simple method to determine the direction of vectors in rotating systems, such as torque, angular velocity, angular acceleration, and angular momentum.
A gyroscope will fall over if it is not spinning due to the lack of angular momentum to resist gravity.
When a gyroscope is spinning, it has angular momentum that resists changes due to gravity, allowing it to maintain an upright position even on a small surface like a cup.
As a gyroscope slows down, it loses angular momentum, and gravity's torque becomes stronger, eventually causing it to topple.
Torque is the application of a force perpendicular to the radius of a rotating system, and its direction can be determined using the right-hand rule.
Angular velocity is the rate of spin of a rotating system, and its vector direction is perpendicular to the plane of rotation.
Angular acceleration is the increase in angular velocity, and like angular velocity, its vector direction is also perpendicular to the plane of rotation.
Angular momentum is a vector quantity that represents the rotational motion of an object, and its direction is determined by the right-hand rule based on the direction of rotation.
A gyroscope's resistance to changes in orientation is due to its angular momentum, which can be observed when it maintains balance on a small surface despite gravity.
The precession of a gyroscope is a result of the combined vectors of its angular momentum and the torque due to gravity.
As a gyroscope spins and precesses, it demonstrates the principles of torque, angular velocity, angular acceleration, and angular momentum in a practical and observable way.
The principles discussed can be explored through hands-on experiments with gyroscopes or larger rotating systems like bicycle wheels, providing a tangible understanding of rotational physics.
Studying rotating systems allows for the analysis of various forces and the collection of data on torque, angular velocity, angular acceleration, and momentum, enhancing comprehension of rotational dynamics.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: