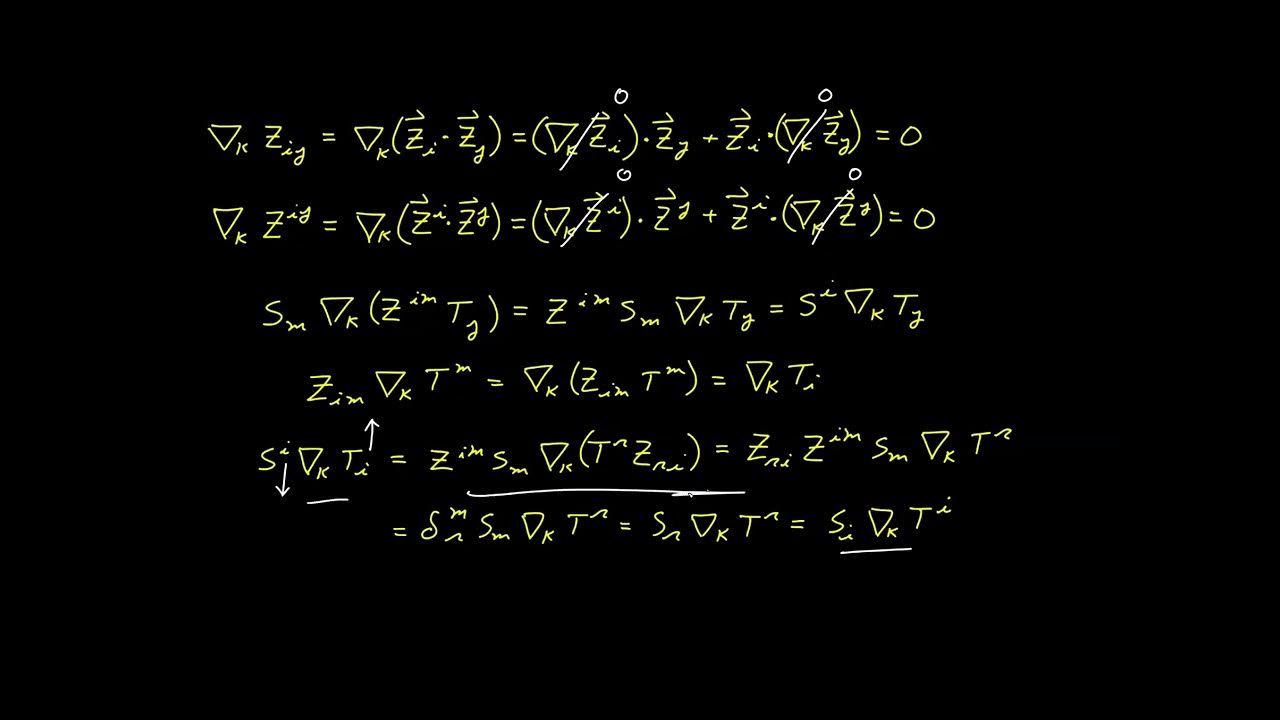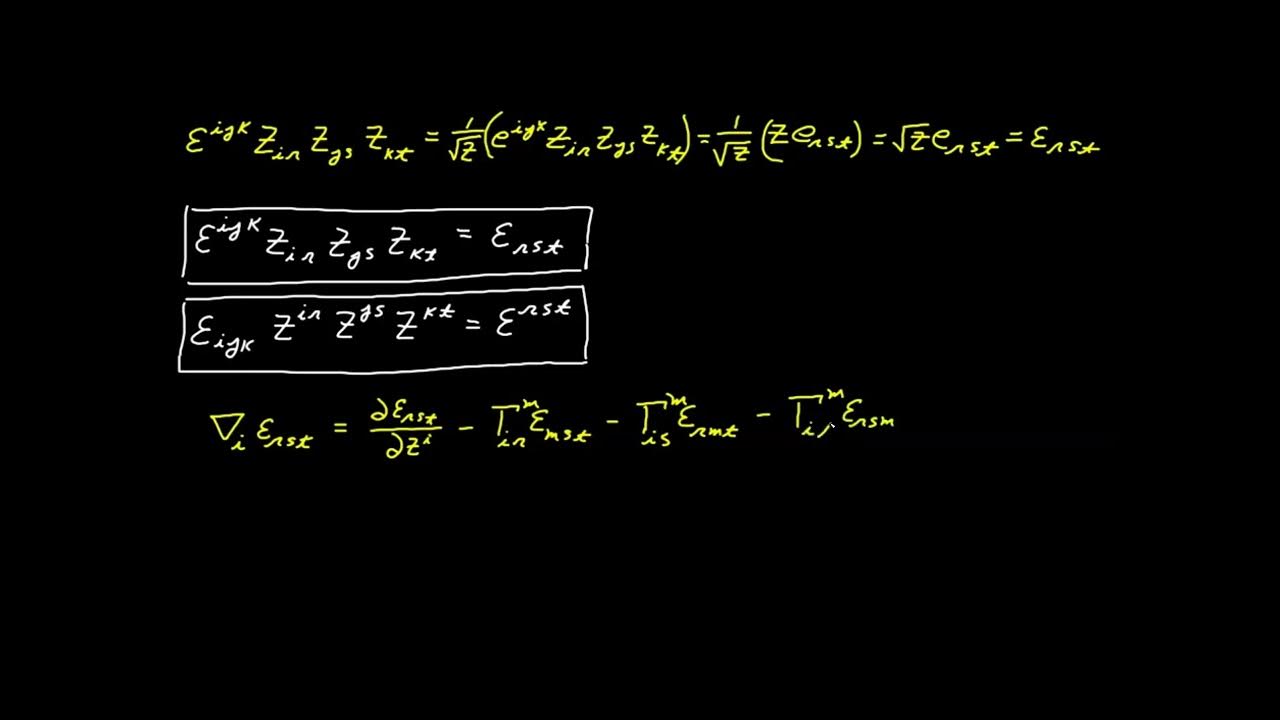Video 45 - Delta System
TLDRThis video introduces the delta system in tensor calculus, a determinant tool used to evaluate expressions involving Kronecker deltas. It explains how to determine non-zero values based on index permutations, identifies tensor properties and metronomic behavior, and demonstrates evaluation rules for different delta expressions. The script also derives important identities and shows the equivalence of the delta system to permutation symbols, offering a comprehensive understanding of its applications in tensor calculus.
Takeaways
- 📚 The script introduces the delta system, a determinant tool in tensor calculus.
- 🔍 It defines the delta expression as the determinant of a matrix with Kronecker delta terms.
- 📉 The expansion of the determinant reveals that terms are non-zero only when all three indices match.
- 🔄 Duplicate indices in the delta expression result in terms that cancel each other out, leading to a zero value.
- 🔢 The delta expression evaluates to either +1 or -1 depending on whether the index permutations are even or odd.
- 🧩 The script shows that the delta system can be applied to both two and three indices, with similar principles.
- 📉 Kronecker deltas are tensors and possess the metronomic property, meaning their covariant derivative is zero.
- 🔑 Important identities are derived, such as the contraction of indices leading to simpler delta expressions.
- 🔄 The script explains that the value of the delta system is determined by the permutation of indices being even or odd.
- 🔗 The delta system can also be defined using permutation symbols, which is equivalent to the determinant-based definition.
- 🔚 The script concludes with a summary of the properties and behaviors of the delta system in tensor calculus.
Q & A
What is the delta system introduced in the video?
-The delta system is a determinant tool used in tensor calculus, defined as the determinant of a matrix composed of Kronecker delta terms.
How is the determinant of the delta system expanded?
-The determinant is expanded by taking three factors at a time to form terms, following the pattern of taking three for the first negative term, three for the next, and so on.
What condition must be met for any term in the delta system expansion to be non-zero?
-For any term to be non-zero, all three factors (indexes) in a Kronecker delta must be equal, and the combination of index values for i, j, and k must be the same as for r, s, and t.
What happens if there are duplicate values among the indexes in the delta system?
-If there are duplicate values among the indexes, the terms will cancel each other out in pairs, resulting in the expression being zero.
What must be true for the indexes i, j, and k in a three-dimensional space when using the delta system?
-In a three-dimensional space, the indexes i, j, and k must be a unique permutation of the numbers one, two, and three.
How does the value of the delta system expression change with permutations of the indexes?
-The value of the expression is positive one if the permutations are even and negative one if they are odd, assuming the indexes are distinct and identical in the upper and lower positions.
What property do the delta expressions possess according to the video?
-The delta expressions possess the metronomic property, meaning their covariant derivative with respect to any index is zero.
What is the relationship between the delta system and the permutation symbol?
-The delta system can be defined as the product of two permutation symbols, where the behavior described for the delta system matches that of the permutation symbols.
What happens when an index in the delta system is contracted?
-When an index is contracted, the resulting expression simplifies to a delta element with fewer indexes, following a pattern from 1 to 2 to 3.
What is the significance of the Kronecker delta in the delta system?
-The Kronecker delta is a fundamental component of the delta system, used to form the determinant and determine the non-zero values of the system.
How can the delta system be used to evaluate expressions with tensor indices?
-The delta system provides a method to evaluate expressions by ensuring that the tensor indices are distinct and identical in their respective positions, and by considering the permutation of these indices.
Outlines
📚 Introduction to the Delta System in Tensor Calculus
The video introduces a fundamental concept in tensor calculus known as the delta system. It begins by defining the delta expression as the determinant of a matrix composed of Kronecker delta terms. The video explains how to expand this determinant and emphasizes that non-zero values occur only when all three factors of the Kronecker delta are equal, which means the index values must match perfectly. The importance of having distinct index values is highlighted, and the concept is illustrated with examples where duplicates lead to cancellation, reinforcing the rule that only unique permutations of index values can yield non-zero results.
🔍 Evaluating Delta Expressions with Unique Index Permutations
This paragraph delves deeper into how to evaluate the delta expressions by considering the permutations of the index values. It explains that the expression evaluates to either +1 or -1 depending on whether the permutations of the index values are even or odd, respectively. Several examples are provided to illustrate this rule, showing how different permutations affect the outcome. The video also touches on the concept of flipping operations and how they relate to even or odd numbers of such operations, which in turn affect the sign of the delta expression.
📘 Tensor Properties and Metronymic Behavior of Delta Expressions
The paragraph discusses the properties of the delta expressions, establishing that they are tensors due to their construction from tensorial Kronecker deltas. It also covers the metronymic property, which states that the covariant derivative of the delta expressions with respect to any index is zero. This is demonstrated through the application of the product rule in taking covariant derivatives, showing that each term in the expansion contains a factor of zero, hence the entire expression's derivative is zero.
🔗 Deriving Key Identities for Delta Expressions
The focus shifts to deriving important identities involving the delta expressions. By performing contractions on the indices, the video shows how the three-index delta expression simplifies to the two-index delta expression, and how further contraction leads to the single Kronecker delta. The pattern observed in these contractions is from 1 to 2 to 3, relating each delta symbol to the next in a clear progression.
📌 Equivalence of Delta System to Permutation Symbols
The video concludes with a discussion on the equivalence of the delta system to permutation symbols. It demonstrates that the delta expressions with their defined behavior can be represented as products of permutation symbols, and vice versa. This equivalence is used to further validate the properties and behaviors discussed earlier in the video, showing that either definition can be used as a basis for understanding the delta system.
📝 Recap and Conclusion of Delta System Properties
In the final paragraph, the video provides a recap of the delta system's properties and behaviors. It reiterates the rules for evaluating delta expressions, the conditions for obtaining non-zero values, and the significance of index permutations. The video also summarizes the derived identities and the equivalence to permutation symbols, reinforcing the comprehensive understanding of the delta system established throughout the video.
Mindmap
Keywords
💡Tensor Calculus
💡Determinant
💡Kronecker Delta
💡Permutation Symbol
💡Delta System
💡Tensor
💡Metric Property
💡Covariant Derivative
💡Permutation
💡Contraction
💡Identity
Highlights
Introduction of the delta system, a useful determinant tool in tensor calculus.
Definition of the delta expression as the determinant of individual Kronecker delta terms.
Expansion of the determinant to understand the evaluation of the new expression.
Explanation of the condition for non-zero terms: matching index values on Kronecker delta factors.
Illustration of term cancellation when duplicate index values occur.
Requirement for unique and identical index value sets for non-zero expression evaluation.
Demonstration of how permutations of index values affect the delta expression's outcome.
Examples showing how the delta expression evaluates to either +1 or -1 based on index permutations.
Clarification that the delta system can be applied to two-index expressions as well.
Analysis of the metronomic property of the delta expressions, showing their covariant derivatives are zero.
Derivation of important identities involving contractions of the delta expressions.
Property that the contraction of a delta with three indexes results in a two-index delta expression.
Pattern observed in contractions, relating to the number of indexes in the delta system.
Equivalence of the delta system to the product of permutation symbols, and its implications.
Recap summarizing the properties, definitions, and evaluation rules of the delta system.
Final relationship between the delta system and permutation symbols, as a basis for further derivation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: