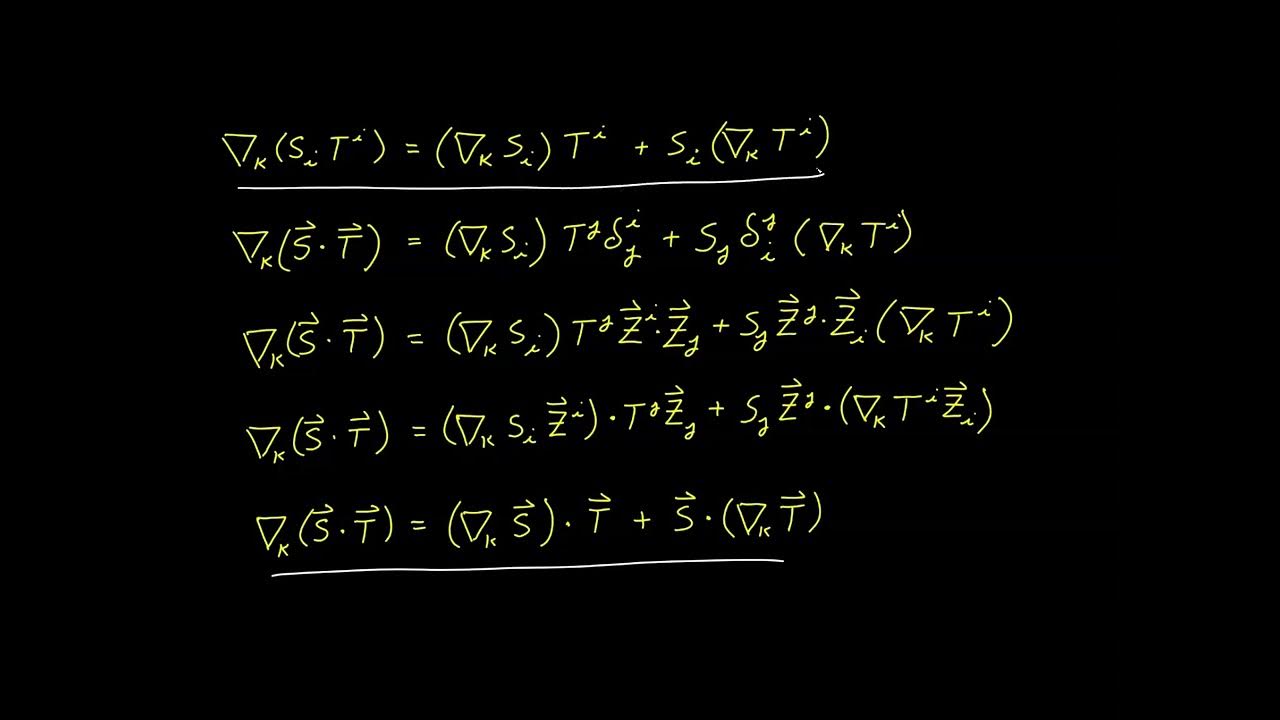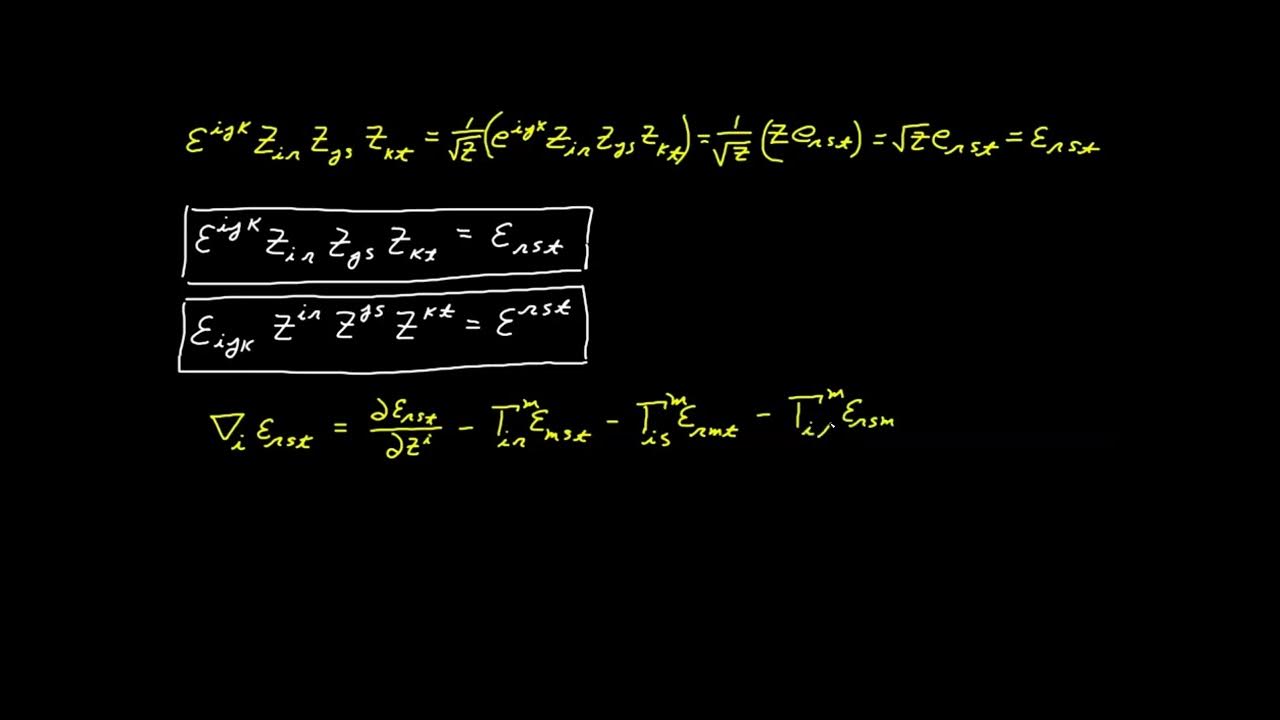Video 38 - Metrinilic Property - Part 2
TLDRIn this video on tensor calculus, the presenter explores the metronic property, demonstrating that the covariant derivative of the Kronecker Delta and metric tensors equals zero, allowing them to move in and out of derivative operations like constants. Practical applications are discussed, such as simplifying expressions involving tensor products and covariant derivatives. The concept of contravariant derivative is introduced, extending the divergence definition and enabling index flipping between operations and operands. Finally, the mixed metric tensor is derived, proving its equivalence to the Kronecker Delta and solidifying its place within the metronic family of tensors.
Takeaways
- 📚 The script discusses the metronic property in tensor calculus, specifically focusing on the covariant derivative of the Kronecker Delta and metric tensors.
- 🔍 It explains that the covariant derivative of the Kronecker Delta function results in zero, indicating it possesses the metronic property, allowing it to move in and out of covariant derivative operations as if it were a constant.
- 📘 The script demonstrates the practical application of the metronic property in simplifying expressions involving the covariant derivative and Kronecker Delta or metric tensors.
- 📐 The covariant and contravariant metric tensors are both shown to have the metronic property, meaning their covariant derivatives equal zero, simplifying operations involving index raising and lowering.
- 👉 The video introduces a new operation, the contravariant derivative, which complements the covariant derivative and allows for the formation of contractions with covariant vector components.
- 🆕 The contravariant derivative is defined as a means to produce a contravariant index from a covariant derivative operation, extending the concept of divergence to include covariant vector components.
- 🔄 The script illustrates how the metronic property enables the flipping of dummy indices, which is a familiar operation in tensor calculus, even when the factors are on opposite sides of the covariant derivative.
- 🔗 The metronic property is highlighted as a key relationship connecting various tensor calculus objects, such as the Kronecker Delta, metric tensors, and the newly introduced mixed metric tensor.
- 📈 The mixed metric tensor is derived and shown to be identical to the Kronecker Delta, reinforcing its connection to the metric tensors and the metronic property.
- 📝 The script concludes with a recap of the metronic property's significance in tensor calculus, emphasizing its role in simplifying operations and the relationships between different tensor objects.
- 🔑 The final observation points out that all objects with the metronic property are related to the metric tensors, either directly or indirectly, highlighting the fundamental role of metric tensors in tensor calculus.
Q & A
What property of the Kronecker Delta function is discussed in the video?
-The video discusses the metronic property of the Kronecker Delta function, which allows it to be moved in and out of covariant derivative operations as if it were a constant.
What is the covariant derivative of the Kronecker Delta function?
-The covariant derivative of the Kronecker Delta function is zero, which means it possesses the metronic property.
Why is the covariant derivative of the basis vectors equal to zero?
-The covariant derivative of the basis vectors is equal to zero due to the metronic property, which implies that the basis vectors are not changing in the coordinate system being used.
What is the practical application of the metronic property when dealing with the covariant derivative of a product involving the Kronecker Delta?
-The metronic property allows the Kronecker Delta factor to be moved outside the covariant derivative operation, simplifying the expression without the need for intermediate steps.
How does the metronic property affect the covariant derivative of metric tensors?
-The metronic property ensures that the covariant derivative of both the covariant and contravariant metric tensors is zero, allowing them to be treated as constants within the covariant derivative operation.
What is the contravariant derivative, and how is it related to the covariant derivative?
-The contravariant derivative is a new operation defined to produce a contravariant index instead of a covariant one. It is related to the covariant derivative by allowing for similar contractions using covariant vector components.
What is the significance of the mixed metric tensor in the context of the metronic property?
-The mixed metric tensor, which has one contravariant and one covariant index, is identical to the Kronecker Delta and is part of the metronic family because it possesses the metronic property.
How does the metronic property simplify the process of flipping dummy indices in tensor calculus?
-The metronic property allows for the direct flipping of dummy indices, even when the factors are on opposite sides of the covariant derivative operation, without the need for intermediate steps.
What is the relationship between the metric tensors and the basis vectors in terms of information content?
-The information content of the metric tensors is roughly equivalent to that of the basis vectors, as the metric tensors are defined in terms of all possible dot products between the basis vectors.
Why is the Kronecker Delta considered part of the metric tensor family?
-The Kronecker Delta is considered part of the metric tensor family because it is identical to the mixed metric tensor, which is directly related to the metric tensors through contractions.
Outlines
🔍 Covariant Derivative of Kronecker Delta and Metric Tensors
In this segment, the video discusses the covariant derivative of the Kronecker Delta function, which is shown to be zero due to the metric property. The covariant derivative is applied to the product of basis vectors, and it's demonstrated that the result is zero because the covariant derivative of each basis vector is zero. This property is then used to simplify expressions involving the covariant derivative of products involving the Kronecker Delta. Practical applications are also explored, such as simplifying expressions with the covariant derivative of a product of Delta and a tensor, where the Delta factor can be moved outside the derivative due to its metric property.
📚 Practical Applications of the Metric Property in Tensor Calculus
This paragraph delves into the practical applications of the metric property in tensor calculus, specifically how it simplifies the process of raising and lowering indices. The video provides examples of how the covariant derivative can eliminate symmetric tensor factors, allowing for the direct manipulation of indices without intermediate steps. The contravariant metric tensor is also discussed, showing that it possesses the same metric property as the covariant metric tensor, and this property is used to simplify expressions involving the covariant derivative of metric tensors.
🆕 Introduction of Contravariant Derivative and Divergence
The video introduces a new operation called the contravariant derivative, which allows for the formation of contractions using covariant vector components. This is contrasted with the covariant derivative, which requires a contravariant vector component. The contravariant derivative is defined in terms of the covariant derivative and the metric tensor, and it is shown to be equivalent to the covariant derivative when contracted with a covariant vector component. The concept of divergence is also extended to include this new operation, allowing for the flipping of indices between the derivative operation and the operand.
🔗 Relationship Between Kronecker Delta, Metric Tensors, and Basis Vectors
This section discusses the relationship between the Kronecker Delta, metric tensors, and basis vectors. It explains how the Kronecker Delta can be related to the metric tensors by considering it as a tensor and performing index raising and lowering operations. The video demonstrates that the Kronecker Delta is identical to a mixed metric tensor, which has both contravariant and covariant indices. This connection reinforces the idea that the Kronecker Delta is part of the metric family of tensors and highlights the fundamental role of metric tensors in tensor calculus.
🔄 The Metronic Property and Its Implications for Tensor Operations
The video concludes by summarizing the metronic property and its implications for tensor operations. It emphasizes that the covariant derivative of the Kronecker Delta and both the covariant and contravariant metric tensors is zero, allowing these tensors to be treated as constants within the covariant derivative operation. This property simplifies the process of flipping indices and performing tensor operations. The video also introduces the concept of the mixed metric tensor and shows its equivalence to the Kronecker Delta, further illustrating the interconnectedness of these tensor calculus objects.
📘 Recap and Understanding of the Metronic Property
In the final paragraph, the video provides a recap of the main points covered regarding the metronic property. It reiterates how the covariant derivative of the Kronecker Delta and metric tensors is zero, and how this property allows for the simplification of tensor expressions. The contravariant derivative is also discussed as a means to extend the definition of divergence and to work with covariant objects more conveniently. The video ends with a clear explanation of why the Kronecker Delta is considered part of the metronic family, tying it back to the fundamental role of metric tensors in tensor calculus.
Mindmap
Keywords
💡Covariant Derivative
💡Kronecker Delta
💡Metronic Property
💡Basis Vectors
💡Product Rule
💡Covariant Basis Vector
💡Contravariant Basis Vector
💡Metric Tensor
💡Divergence
💡Mixed Metric Tensor
Highlights
Introduction of the covariant derivative of the Kronecker Delta function and its metronic property.
Explanation of the product rule for covariant derivatives and its application to basis vectors.
Demonstration that the covariant derivative of basis vectors equals zero, simplifying expressions.
Practical application of the metronic property in simplifying covariant derivatives involving the Kronecker Delta.
Illustration of how the metronic property allows for the movement of the Delta factor in and out of covariant derivatives.
Introduction of the covariant derivative of the covariant metric tensor and its metronic property.
Application of the metronic property to metric tensors in raising and lowering indices.
Explanation of how the metronic property simplifies the process of flipping indexes in tensor calculus.
Introduction of the contravariant derivative, a new operation for handling covariant vector components.
Definition and application of the contravariant derivative in forming contractions.
Extension of the divergence definition to include the contravariant derivative.
Observation that the covariant derivative of metric tensors is zero, indicating their metronic property.
Discussion on the relationship between metric tensors and basis vectors, emphasizing their informational equivalence.
Introduction of the mixed metric tensor and its equivalence to the Kronecker Delta.
Explanation of how the mixed metric tensor is derived and its role in tensor calculus.
Final observation on the metronic property's applicability to various tensor calculus objects and their relation to metric tensors.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: