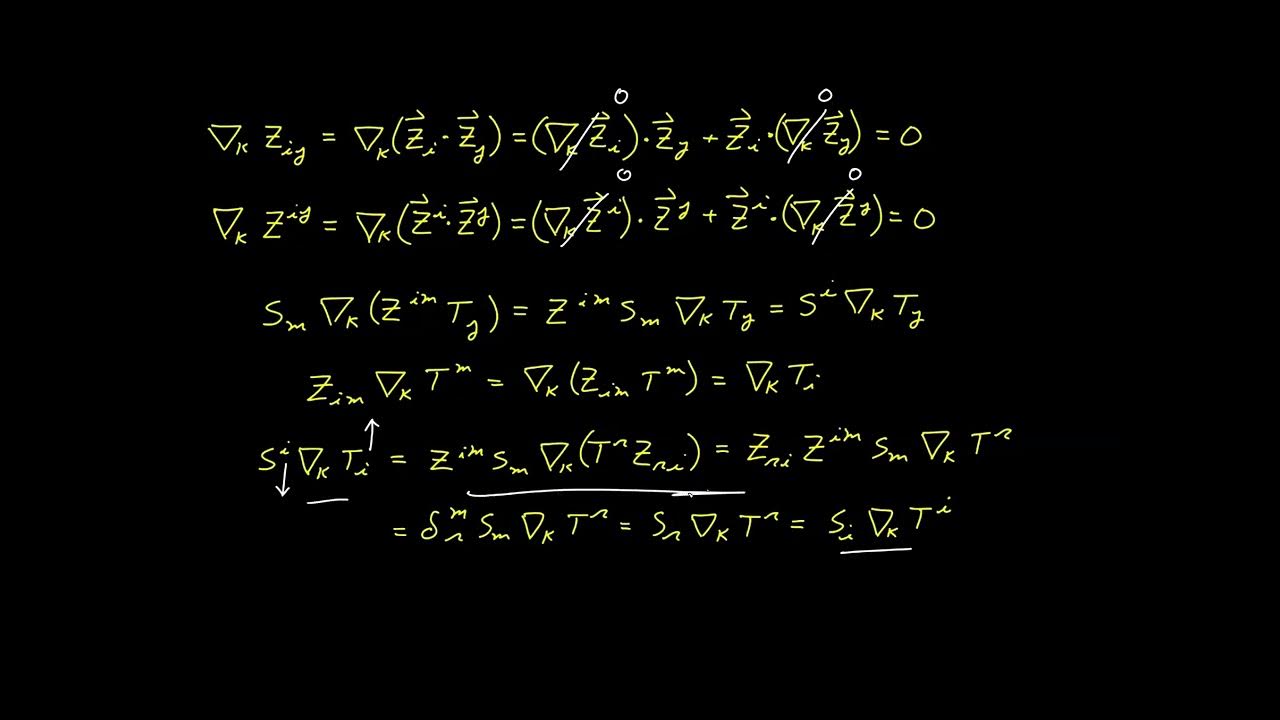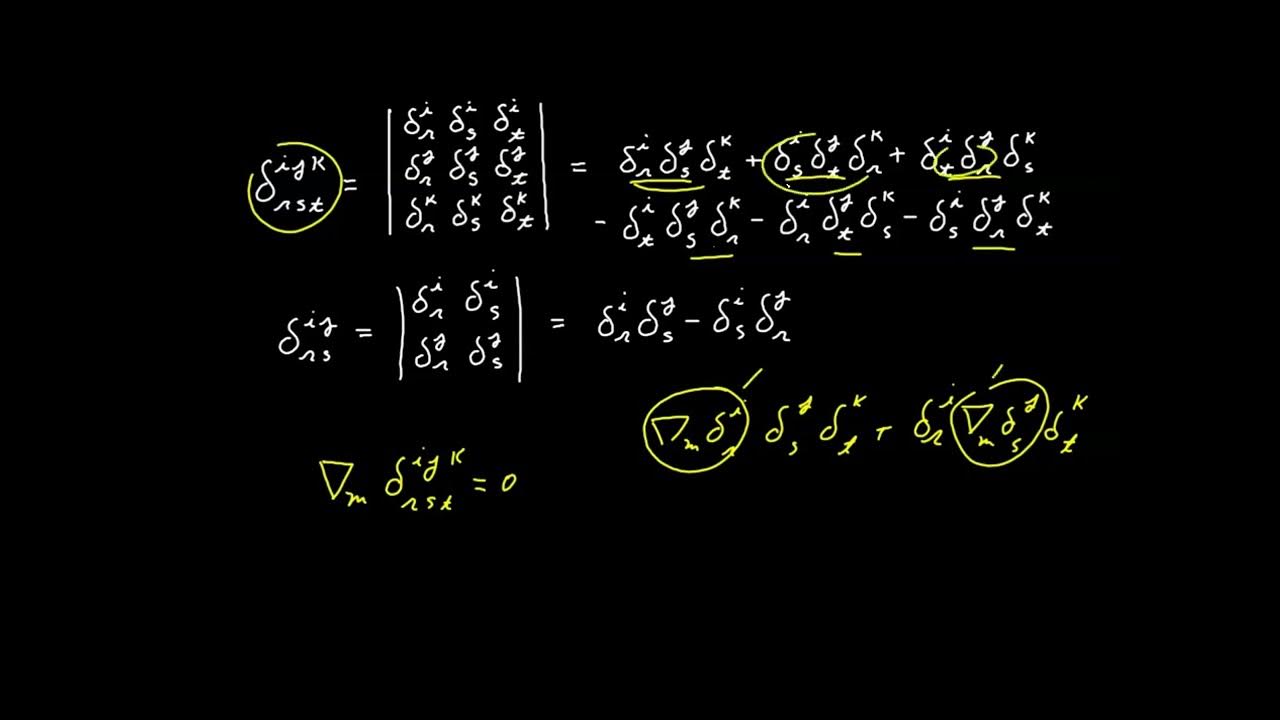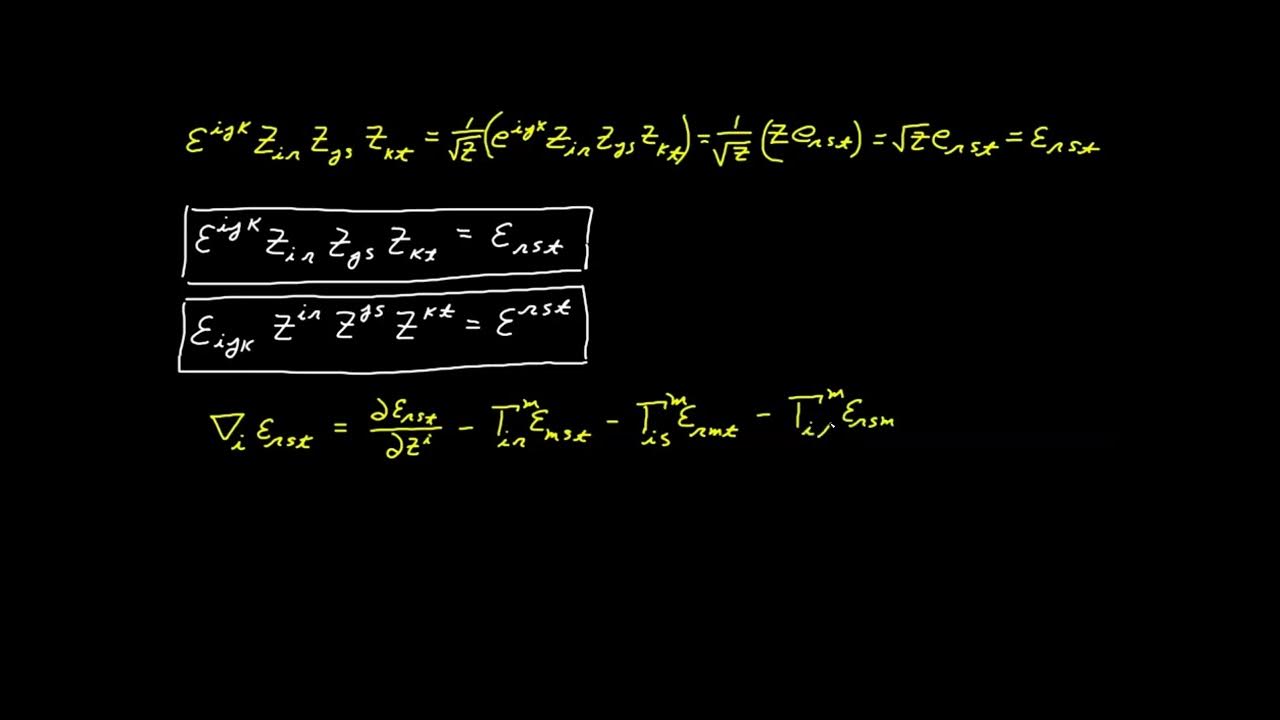Video 13 - Kronecker Delta
TLDRIn this 13th installment of the tensor calculus series, the presenter introduces the Kronecker delta function, a fundamental tool in tensor calculus. The video demonstrates the creation of a composite function involving z as a function of itself and explores the partial derivatives that arise. The Kronecker delta is defined as a function that equals one if its indices match and zero otherwise. The presenter illustrates how the product of a Jacobian matrix and its inverse results in the Kronecker delta, emphasizing its role in simplifying tensor expressions. The video concludes with examples of how the Kronecker delta absorbs indices, facilitating transformations between coordinate systems.
Takeaways
- 📚 The video introduces the Kronecker delta function, a fundamental component in tensor calculus.
- 🔄 The Kronecker delta is defined as a function equal to 1 when the upper and lower indices are the same, and 0 when they differ.
- 🤔 The script explores the concept of a composite function where a variable is considered a function of itself, leading to a complex expression with multiple free indices.
- 🧩 The partial derivatives of the composite function are calculated, resulting in expressions involving the Jacobian and its inverse.
- 📉 The Jacobian matrix and its inverse are shown to be multiplicative inverses of each other, a key property in tensor calculus.
- 🎛 The Kronecker delta is likened to the identity matrix in linear algebra, playing a similar role in simplifying tensor expressions.
- 📝 The script demonstrates the Kronecker delta's ability to 'absorb' an index, simplifying expressions by eliminating terms where the indices do not match.
- 🌐 The video uses the example of converting between Cartesian and polar coordinates to illustrate the application of the Kronecker delta in transforming tensors.
- ↔️ It is shown that the Kronecker delta can be used to invert the perspective of a covariant transformation from unprimed to primed coordinates and vice versa.
- 🔢 The Kronecker delta is a second-rank tensor, with one covariant and one contravariant index, which is crucial for its role in tensor calculus.
- 📚 The video concludes by emphasizing the importance of the Kronecker delta in tensor calculus and its correct representation in various disciplines.
Q & A
What is the Kronecker delta function?
-The Kronecker delta function, denoted as δ_ij, is a mathematical function that equals 1 when the indices i and j are the same and 0 when they are different. It is used in tensor calculus and has properties similar to the identity matrix in linear algebra.
How is the Kronecker delta function related to the Jacobian matrix?
-The Kronecker delta function can be obtained by multiplying a Jacobian matrix by its inverse. This results in a matrix where all off-diagonal elements are zero and the diagonal elements are one, which is the definition of the Kronecker delta.
What does it mean for the Kronecker delta to absorb an index?
-When the Kronecker delta is used in an expression with a dummy index, it effectively 'absorbs' that index, reducing the expression to a single term where the dummy index is replaced by the free index. This simplifies the expression by eliminating terms that would otherwise be zero.
Why is the order of indices in the Kronecker delta function important?
-The order of indices in the Kronecker delta is important because it determines which index is absorbed when used in expressions involving summation. The index that is to be absorbed must be opposite the one that is being summed over.
How does the Kronecker delta function simplify tensor transformations?
-The Kronecker delta function simplifies tensor transformations by reducing expressions involving sums over dummy indices. It allows for the direct substitution of the free index in place of the dummy index, simplifying the transformation equations.
What is the significance of the Kronecker delta being a second-rank tensor?
-The Kronecker delta being a second-rank tensor means it has one covariant and one contravariant index. This property is crucial for tensor calculus as it allows the Kronecker delta to be used in various tensor operations, including raising and lowering indices.
Can the Kronecker delta be represented differently in other disciplines?
-Yes, in some disciplines such as engineering and physics, the Kronecker delta may be represented without the distinction of upper and lower indices. However, this representation is not suitable for tensor calculus, which requires the specific index positions to function correctly.
What is the identity matrix and how is it related to the Kronecker delta?
-The identity matrix is a square matrix in which all the elements of the principal (main) diagonal are ones and all other elements are zeros. It is related to the Kronecker delta in that the Kronecker delta can be represented as an identity matrix, and it plays a similar role in tensor calculus as the identity matrix does in linear algebra.
How does the Kronecker delta function simplify the computation of partial derivatives in tensor calculus?
-The Kronecker delta function simplifies the computation of partial derivatives by allowing for the direct substitution of indices in expressions where the derivative of a variable with respect to itself is 1, and with respect to another variable is 0, thus reducing the complexity of the calculations.
What are the implications of the Kronecker delta being used in covariant and contravariant transformations?
-The use of the Kronecker delta in both covariant and contravariant transformations allows for the inversion of these transformations. It provides a consistent way to switch between coordinate systems in tensor calculus, maintaining the integrity of the transformations regardless of the direction (from unprimed to primed or vice versa).
Outlines
📚 Introduction to the Kronecker Delta Function
In this segment, the video introduces the Kronecker Delta function, a fundamental concept in tensor calculus. The explanation begins with the creation of a composite function involving 'z' as a function of itself, leading to a complex expression with multiple free indices. The focus then shifts to calculating partial derivatives and the importance of the Jacobian in understanding transformations between coordinate systems. The Kronecker Delta function is defined as a function that equals one if its indices are identical and zero otherwise, simplifying the expression of partial derivatives and establishing its role as an identity element in tensor calculus.
🔍 Exploring the Kronecker Delta as a Matrix
This paragraph delves into the representation of the Kronecker Delta as a matrix, specifically the identity matrix, in the context of tensor calculus. The discussion highlights how the Kronecker Delta simplifies expressions involving Jacobians and their inverses, demonstrating that their product results in the identity matrix. The video provides a step-by-step guide to constructing the Kronecker Delta matrix and illustrates its properties with examples from linear algebra, emphasizing its role as an identity element in matrix multiplication.
📈 Matrix Multiplication and Inverse Jacobians
The video script continues with an exploration of matrix multiplication involving Jacobians and their inverses. It explains how the Kronecker Delta emerges from the product of a Jacobian and its inverse, regardless of the order of multiplication due to their inverse relationship. The script includes a practical example using plane polar coordinates to demonstrate the calculation and the resulting identity matrix. This section reinforces the concept that the Kronecker Delta can absorb indices, simplifying covariant transformations between coordinate systems.
🔄 Covariant Transformations and Index Absorption
This paragraph discusses the application of the Kronecker Delta in covariant transformations, illustrating how it can absorb indices to simplify expressions. The video provides examples of how the Kronecker Delta functions in both primed and unprimed coordinate systems, showing that it can be used to transform between these systems. The concept of index absorption is further clarified with examples, demonstrating how the Kronecker Delta simplifies tensor expressions by eliminating terms where the indices do not match.
🎓 Tensor Properties and Kronecker Delta Index Positions
The final paragraph of the script addresses the tensor properties of the Kronecker Delta, explaining why its indices must be positioned in either upper or lower cases to function correctly within tensor calculus. It clarifies that the Kronecker Delta is a second-rank tensor, being covariant in one index and contravariant in the other, which is essential for its role in various tensor operations. The video also warns against the misuse of alternative notations of the Kronecker Delta in tensor calculus and concludes with a review of key takeaways from the lesson.
Mindmap
Keywords
💡Tensor Calculus
💡Kronecker Delta Function
💡Composite Function
💡Partial Derivative
💡Jacobian
💡Transformation Relationship
💡Dummy Index
💡Identity Matrix
💡Covariant Transformation
💡Matrix Multiplication
💡Absorption of Index
Highlights
Introduction to the Kronecker delta function, a fundamental addition to tensor calculus.
Creation of a composite function where a variable is expressed as a function of itself, leading to a unique tensor calculus setup.
Differentiation of the composite function to explore partial derivatives with multiple free indices.
Identification of the Jacobian matrix within the expressions derived from the composite function.
Explanation of the Kronecker delta function as a binary function with values of 0 or 1 based on index equality.
Demonstration of the Kronecker delta function's role as an identity matrix in tensor calculus.
Matrix representation of the Kronecker delta, highlighting its properties in a 3x3 matrix form.
Illustration of the Kronecker delta's ability to absorb indices in tensor expressions.
Application of the Kronecker delta in transforming between coordinate systems using the Jacobian and its inverse.
Example calculation using plane polar coordinates to demonstrate the Kronecker delta's utility in matrix multiplication.
Discussion on the commutative property of matrix multiplication involving the Jacobian and its inverse.
Insight into the Kronecker delta's behavior in different coordinate dimensions and its generalizability.
Explanation of how the Kronecker delta simplifies covariant transformations between coordinate systems.
Illustration of the Kronecker delta's contravariant properties in tensor expressions.
Clarification on the positioning of indices in the Kronecker delta for proper tensor calculus operations.
Differentiation between tensor calculus and other disciplines where the Kronecker delta may appear differently.
Review of key takeaways, emphasizing the Kronecker delta's definition, properties, and applications in tensor calculus.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: