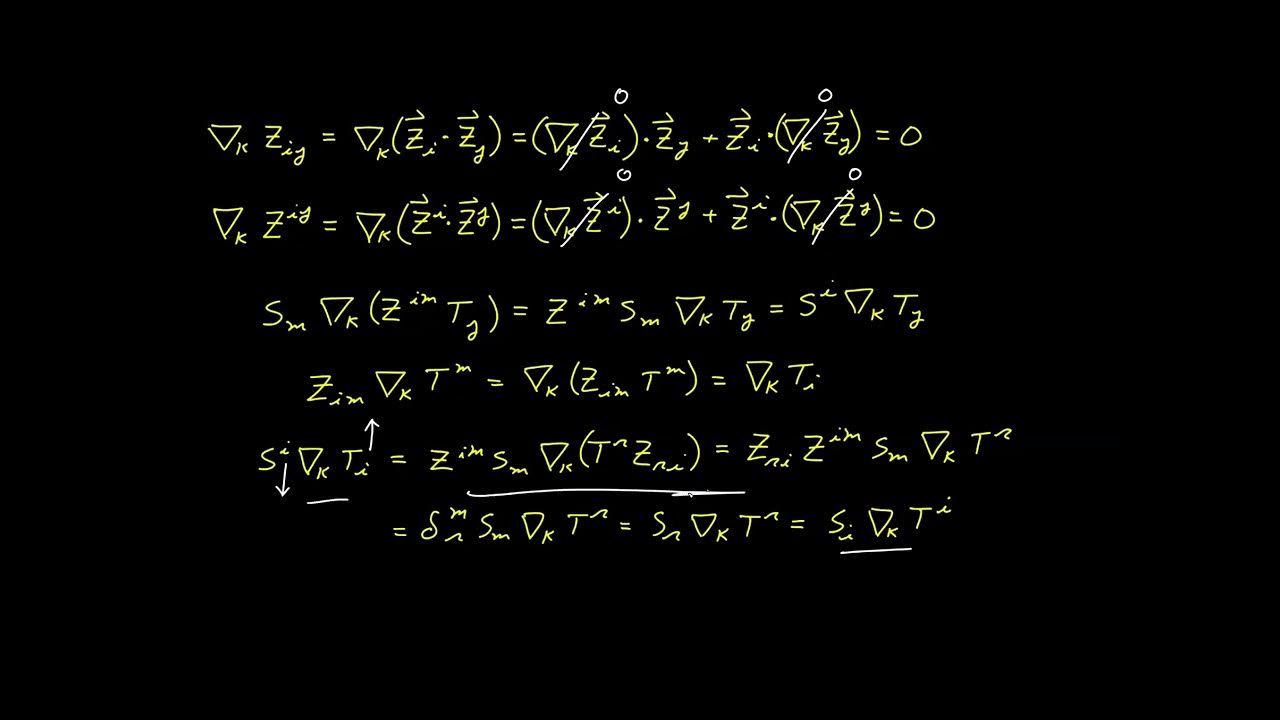Tensor Calculus 4c: A Few Tensor Notation Exercises
TLDRThis educational video script introduces the concept of tensors, a fundamental tool in physics and engineering, with a focus on tensor notation and manipulation. The instructor guides viewers through exercises to practice tensor operations, explains the role of dummy and live indices, and clarifies the use of Kronecker Delta in tensor expressions. The script also touches on the relationship between covariant and contravariant bases, and the representation of vectors. The discussion aims to solidify understanding of tensor notation before delving into more complex topics such as tensor calculus.
Takeaways
- 📚 The session is focused on learning about tensors and manipulating tensor notation.
- 🔍 Exercises are provided to practice tensor notation, emphasizing the importance of understanding summation and index notation.
- 📉 The concept of dummy and live indices is introduced, with live indices needing to match on both sides of an equation for tensor contraction.
- 🎯 Kronecker Delta (\(\delta_{ij}\)) is explained, serving as an index renamer and being absorbed into the terms it contracts with.
- 🧠 The importance of evaluating and analyzing tensor expressions to understand their meaning and implications is stressed.
- 📈 The script covers how to interpret tensor expressions in different scenarios, such as when indices are contracted or when they represent vectors.
- 📚 It is clarified that tensor notation can be abstract, and understanding the underlying algebraic operations is crucial.
- 🧬 The relationship between tensor notation and matrix multiplication is explored, with the script highlighting the differences and similarities.
- 🔄 The script discusses the manipulation of tensor expressions to isolate variables, such as finding \( X_j \) in a given tensor equation.
- 📐 The concept of metric tensors and their properties, such as being inverses of each other, is briefly introduced.
- 🤔 The session ends with a reminder of the importance of understanding tensor notation for further studies in more advanced topics.
Q & A
What is the significance of the Kronecker Delta in tensor notation?
-The Kronecker Delta, denoted as Delta_ij, is a tensor that is used to rename indices in tensor expressions. It is equal to 1 when its indices are the same and 0 otherwise. It is often used to simplify expressions by absorbing indices during contractions.
What does the expression T_j represent after simplification using the Kronecker Delta?
-The expression T_j represents a sum over a tensor T_i with the Kronecker Delta, which simplifies to T_1 when j=1, T_2 when j=2, and T_3 when j=3. Essentially, it captures the component of the tensor T corresponding to the index j.
Why is the Kronecker Delta often not seen with an explicit Delta when manipulating indices?
-The Kronecker Delta is almost never seen with an explicit Delta because it is typically contracted with another tensor, and in such cases, it gets absorbed into the tensor it is contracted with, effectively renaming the indices.
What does it mean for a tensor to have a covariant basis with subscripts?
-A tensor with a covariant basis having subscripts implies that the components of the tensor are expressed with respect to the covariant basis. These components would appear with an upper index, indicating the contravariant basis.
How does the placement of an index affect the interpretation of a tensor?
-The placement of an index, whether it is a subscript or a superscript, determines the type of tensor and its transformation properties under coordinate changes. Upper indices typically represent contravariant vectors, while lower indices represent covariant vectors.
What is the relationship between the Kronecker Delta and the summation notation in tensor expressions?
-The Kronecker Delta is used to implicitly perform a summation over an index. When the same index appears both as a subscript and a superscript, it implies a summation over that index, according to the Einstein summation convention.
Why might the script suggest that matrix notation can be clearer than tensor notation for certain operations?
-Matrix notation can be clearer for certain operations because it allows for a more straightforward visualization of the algebraic manipulations involved, especially when dealing with concepts from linear algebra such as matrix multiplication and inversion.
What is the purpose of the tensor expression a_i_j * b^j_k = Delta^i_k?
-This tensor expression represents the condition where two second-order tensors (matrices) are inverses of each other. The contraction of the tensors on the indices j results in the Kronecker Delta, indicating that the matrices are inverses.
How can one manipulate the expression a_i_j * x^j to isolate x^j?
-To isolate x^j, one can multiply both sides of the expression by the inverse of the matrix represented by a_i_j, effectively using the property that a_i_j * a^(-1)^j_k = Delta^i_k to absorb the Delta and leave x^j.
What is the difference between tensor notation and matrix notation when it comes to the order of multiplication?
-In tensor notation, the order of multiplication does not matter due to the commutative property of scalar multiplication. However, in matrix notation, the order is crucial because matrix multiplication is not commutative, and the dimensions of the matrices must be compatible.
Why is it valid to rename an index in a tensor expression?
-Renaming an index in a tensor expression is valid as long as the new index represents the same set of values and relationships as the original index. It is a way to simplify expressions or to match indices for contraction without changing the underlying meaning of the expression.
Outlines
📚 Introduction to Tensors and Notation Exercises
The script begins with an introduction to the concept of tensors, setting the stage for a series of exercises designed to familiarize the audience with tensor notation. The first exercise involves evaluating an expression with a summation over indices, emphasizing the importance of understanding dummy and live indices in tensor operations. The explanation clarifies that the Kronecker Delta function, represented by 'Delta', is used to simplify expressions by absorbing indices, effectively reducing the complexity of tensor relationships. The summary also touches on the representation of vectors with indices, highlighting the difference between covariant and contravariant bases and how they are denoted with upper and lower indices, respectively.
🔍 Deep Dive into Tensor Index Manipulation
This paragraph delves deeper into the manipulation of tensor indices, using the Kronecker Delta to illustrate how indices can be renamed through contraction. It explains the concept of summation over repeated indices and how it leads to the simplification of tensor expressions. The script uses the Delta function to show how tensor expressions can be simplified to reveal underlying relationships, such as the trace of a matrix or a list of numbers. The summary also addresses common misconceptions about tensor notation and emphasizes the importance of understanding the rules of index summation and contraction, which are fundamental to tensor calculus.
🧩 Exploring Second-Order Tensor Systems and Matrix Inversion
The script introduces second-order tensor systems, which can be visualized as matrices, and discusses the concept of inverse matrices in the context of tensor notation. It presents an exercise where two matrices are inverses of each other and demonstrates how to manipulate these systems using the Kronecker Delta to isolate a vector component. The explanation clarifies that certain tensor operations are more effectively performed using matrix notation due to its algebraic clarity. The summary also touches on the algebraic manipulation of tensor expressions and how they can be simplified to reveal the underlying relationships between matrices and vectors.
📘 Understanding Tensor Notation vs. Matrix Notation
The final paragraph contrasts tensor notation with matrix notation, highlighting the advantages and disadvantages of each in the context of algebraic manipulation. It discusses the process of isolating a variable in a tensor expression and how the order of operations can affect the outcome in matrix notation but not in tensor notation. The script emphasizes the importance of maintaining the integrity of the expression's meaning when renaming indices. The summary reinforces the idea that while tensor notation is powerful, matrix notation can sometimes provide a clearer understanding of the algebraic relationships at play.
Mindmap
Keywords
💡Tensor
💡Gradient
💡Dummy Index
💡Live Index
💡Chroner Delta
💡Covariant Basis
💡Contravariant Basis
💡Matrix
💡Tensor Notation
💡Linear Algebra
Highlights
Introduction to tensor notation and its importance in understanding tensor operations.
Explanation of dummy and live indices in tensor expressions and their role in summation.
Demonstration of how to evaluate and simplify tensor expressions using Kronecker Delta properties.
Clarification on the use of tensor notation for vectors and the distinction between covariant and contravariant bases.
Discussion on the placement of indices in tensor notation and its implications for vector representation.
Exercise to practice tensor notation with Kronecker Delta and its role in tensor contraction.
Exploration of the concept of summation in tensor notation and how it relates to matrix operations.
Illustration of how to manipulate tensor expressions to isolate variables, using Delta notation as an example.
Introduction of second-order tensor systems and their relationship to matrices and matrix inverses.
Exercise involving the manipulation of tensor expressions to find the components of a vector.
Comparison between tensor notation and matrix notation, highlighting the advantages of each in different contexts.
Discussion on the algebraic manipulation of tensor expressions and its relation to linear algebra principles.
Explanation of tensor contraction using Kronecker Delta and its equivalence to matrix multiplication.
Clarification on the renaming of indices in tensor notation and its validity in maintaining the expression's meaning.
Introduction to the concept of tensors and their significance in advanced mathematical and physical theories.
Summary of the key points covered in the session on tensor notation and their practical applications.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: