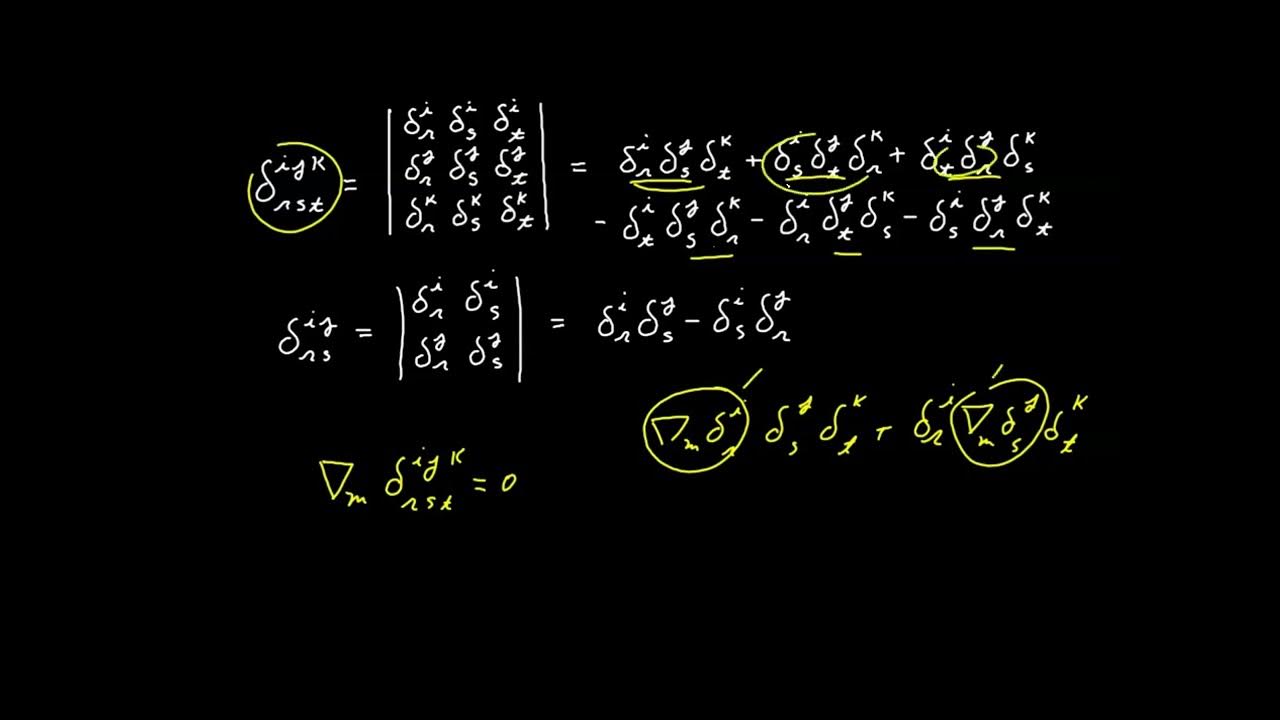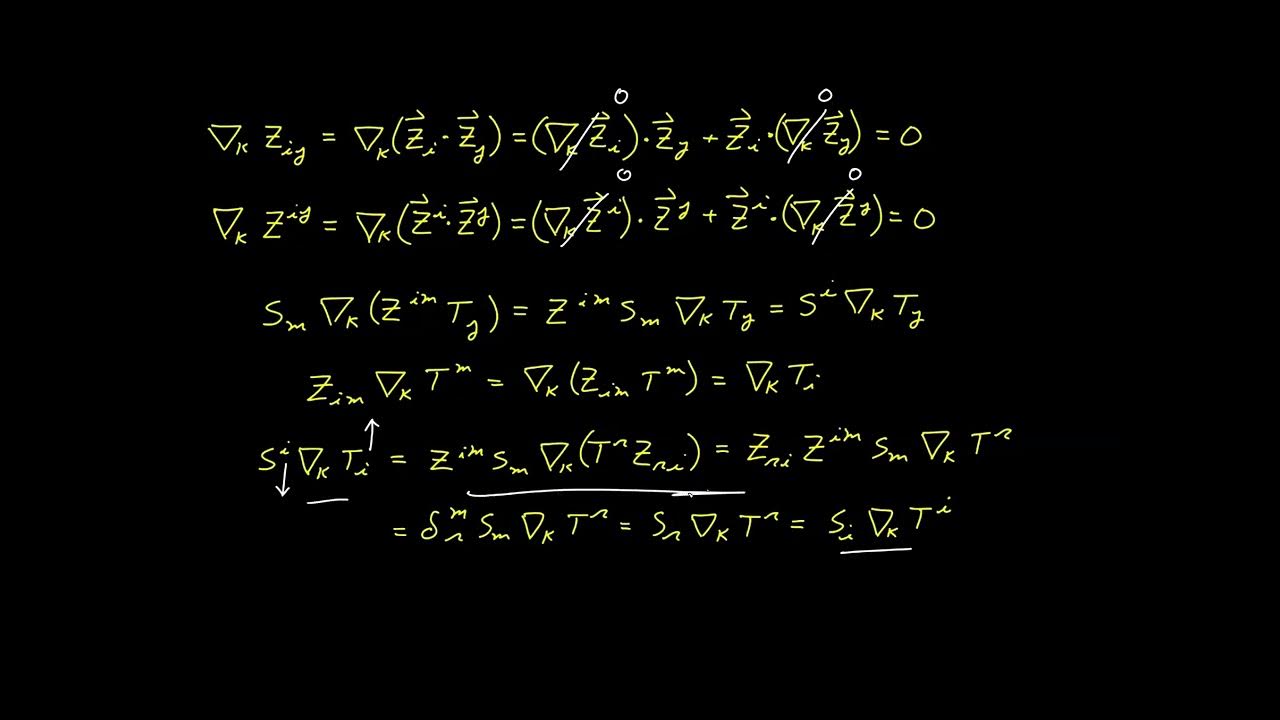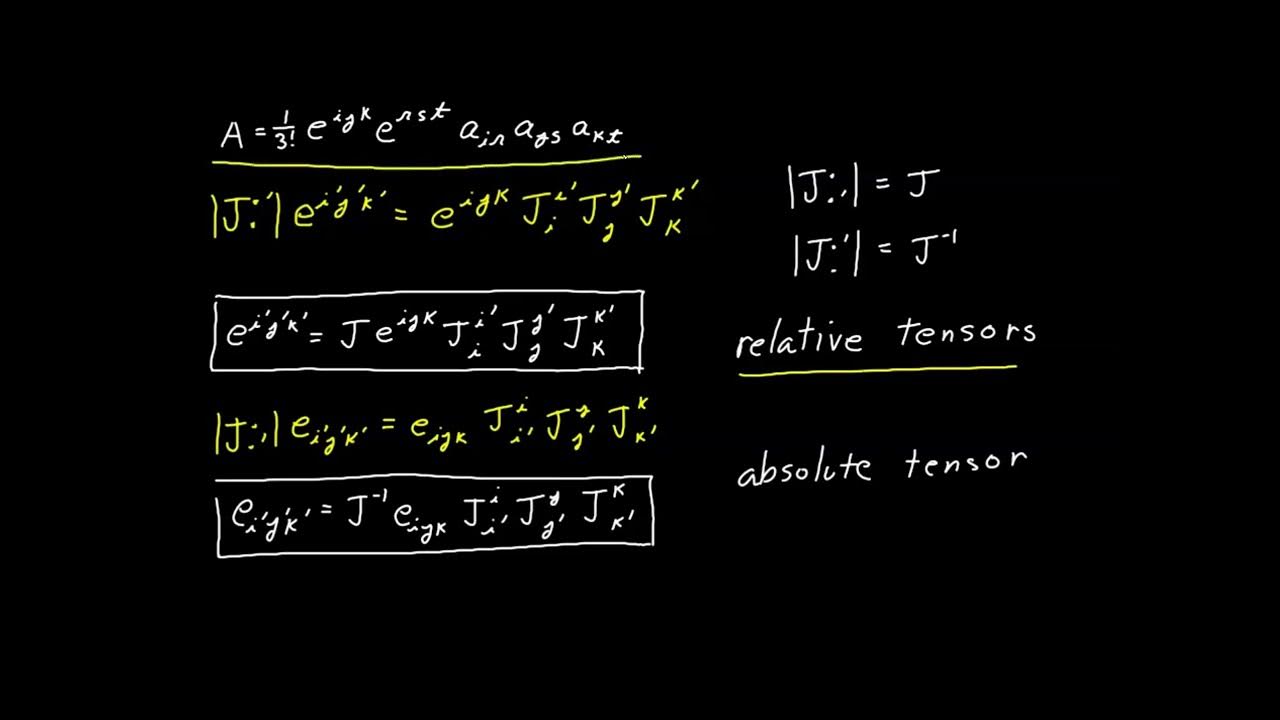Video 51 - Levi Civita Symbols
TLDRIn this 51st video of the tensor calculus series, the concept of Levi-Civita symbols is introduced as absolute tensors, distinct from permutation symbols. The video explains how these symbols, when used with orientation preserving transformations, eliminate the need for weighted factors, thus simplifying tensor operations. It also explores the properties of Levi-Civita symbols, including their skew symmetry, ability to represent the delta function, and their metronomic property, where their covariant derivative equals zero. The video concludes by emphasizing the utility of these symbols in advanced tensor calculus operations.
Takeaways
- 📚 The video introduces Levi-Civita symbols as new tensor calculus objects, which are defined differently from permutation symbols by the inclusion of specific factors.
- 🔍 Levi-Civita symbols are absolute tensors with respect to orientation preserving transformations, meaning they behave consistently when the coordinate systems involved have the same orientation (either both right-handed or both left-handed).
- 🔄 If the coordinate systems have different orientations, a negative sign is inserted in transformations involving Levi-Civita symbols.
- 📉 The script explains how to derive the Levi-Civita symbols from the combination of permutation symbols and volume elements, considering the Jacobian factors.
- 📝 The properties of Levi-Civita symbols are explored, including their skew symmetry with respect to their indices, similar to permutation symbols.
- 🧩 The script demonstrates that the product of two Levi-Civita symbols can represent the Kronecker delta function, providing further confirmation of the tensorial nature of the delta function.
- ⤴️ The video shows how to raise and lower indices of Levi-Civita symbols using covariant and contravariant metric tensors, just as with any other tensor.
- 🔎 The covariant derivative of the Levi-Civita symbols with lower indices is calculated, leading to the definition of a new object, t-i-r-s-t, which is shown to be anti-symmetric with respect to certain index permutations.
- 📌 The anti-symmetry of t-i-r-s-t is proven for all permutations of indices, highlighting that it is a fully anti-symmetric tensor.
- 🎯 The final result for t-i-r-s-t is derived, showing its relationship with the Christoffel symbols and the permutation symbol for specific index values.
- 📚 The video concludes by demonstrating that Levi-Civita symbols possess the metronomic property, meaning their covariant derivatives are zero, which is a characteristic of tensors in curved spaces.
Q & A
What are Levi-Civita symbols?
-Levi-Civita symbols, also known as permutation symbols, are tensor calculus objects that are defined as a product of the volume element and the permutation symbols, adjusted for the orientation of coordinate systems. They are absolute tensors with respect to orientation preserving transformations.
Why are permutation symbols not absolute tensors?
-Permutation symbols are not absolute tensors because they have weights of one and negative one, which makes them relative tensors due to the presence of factors that affect their transformation properties under changes of coordinates.
What is the significance of the volume element in the context of relative tensors?
-The volume element is a relative tensor due to the presence of a Jacobian factor. Its transformation properties are not absolute, which is why it is considered a relative tensor.
How do Levi-Civita symbols relate to the concept of orientation preserving transformations?
-Levi-Civita symbols are absolute tensors with respect to orientation preserving transformations, meaning they maintain their tensorial properties when the coordinate transformations between two systems have the same orientation (both right-handed or both left-handed).
What happens to Levi-Civita symbols when coordinate systems have different orientations?
-If the coordinate systems have different orientations (one is right-handed and the other is left-handed), a negative sign must be inserted in the transformation equations involving Levi-Civita symbols to maintain their tensorial properties.
What property do Levi-Civita symbols possess that permutation symbols do not?
-Levi-Civita symbols possess the metronomic property, meaning their covariant derivatives are zero. This property is not generally true for permutation symbols.
How can the Levi-Civita symbols be used to express the Kronecker delta function?
-The Kronecker delta function can be expressed as the product of two Levi-Civita symbols, demonstrating that it is a tensor due to the tensorial nature of the Levi-Civita symbols.
What is the relationship between the Levi-Civita symbols and the metric tensor when raising and lowering indices?
-Levi-Civita symbols can have their indices raised or lowered using the metric tensor factors, similar to how it is done for other tensors, which further confirms their tensorial properties.
What is the significance of the metronomic property for Levi-Civita symbols?
-The metronomic property, where the covariant derivative of Levi-Civita symbols is zero, indicates that these symbols are invariant under coordinate transformations, which is a key characteristic of tensors.
How do the properties of Levi-Civita symbols contribute to tensor calculus operations?
-The properties of Levi-Civita symbols, such as being absolute tensors under orientation preserving transformations and possessing the metronomic property, make them essential tools in tensor calculus for performing operations like raising and lowering indices and proving tensorial identities.
Outlines
📚 Introduction to Levi-Civita Symbols
This paragraph introduces the concept of Levi-Civita symbols in the context of tensor calculus. It explains that these symbols are absolute tensors, unlike permutation symbols, which are relative. The Levi-Civita symbols are defined in relation to the orientation of coordinate systems, with a plus or minus sign to account for different orientations. The paragraph also discusses how these symbols can be derived by combining permutation symbols with Jacobian factors, leading to a cancellation of orientation-dependent factors and resulting in absolute tensors under orientation-preserving transformations.
🔍 Properties and Tensorial Nature of Levi-Civita Symbols
The second paragraph delves into the properties of Levi-Civita symbols, highlighting their absolute tensorial nature and skew symmetry similar to permutation symbols. It also demonstrates how the Levi-Civita symbols can be used to express the Kronecker delta function in a new way, confirming the tensorial property of the delta function. The paragraph further explores the ability to raise and lower indices using the covariant and contravariant metric tensors, a process that is unique to tensors, thus reinforcing the tensorial nature of the Levi-Civita symbols.
📘 Covariant Derivative of Levi-Civita Symbols
This section investigates the covariant derivative of the Levi-Civita symbols with lower indexes. It applies the rules of covariant differentiation, introduces a new object 't-i-r-s-t' for convenience, and demonstrates that the covariant derivative of the Levi-Civita symbol results in a cancellation, leading to a zero outcome. The paragraph also discusses the anti-symmetry properties of the newly defined object with respect to different index pairs, which is a key characteristic of the Levi-Civita symbols.
🔄 Anti-Symmetry and Index Permutation
The fourth paragraph continues the exploration of the anti-symmetry of the Levi-Civita symbols, specifically focusing on the permutation of the second and third indexes, and then the last two indexes. It shows that the Levi-Civita symbols are completely anti-symmetric with respect to these index pairs, which implies that the expression becomes zero if any of the indexes are duplicates. The paragraph also discusses the implications of this anti-symmetry on the evaluation of the symbols, concluding that there is only one degree of freedom for the indexes r, s, and t.
📐 Generalization and Metronic Property
The fifth paragraph generalizes the result for the anti-symmetric expression 't i r s t' and demonstrates that the covariant derivative of the Levi-Civita symbols with lower indexes is zero, indicating the metronic property. It also shows that the covariant derivative of the delta function, expressed as a product of two Levi-Civita symbols, is zero, confirming the metronic property for symbols with upper indexes as well. This paragraph concludes that the Levi-Civita symbols, both with upper and lower indexes, are indeed metronomic objects.
🚀 Conclusion and Future Applications
In the final paragraph, the video script summarizes the findings of the video, reiterating the definition of the Levi-Civita symbols and their properties as absolute tensors under orientation-preserving transformations. It also highlights the key properties derived, such as the expression of the delta function, the ability to raise and lower indices, and the metronic property of the symbols. The paragraph concludes by setting the stage for future videos where these symbols will be used to define additional tensor calculus operations.
Mindmap
Keywords
💡Tensor Calculus
💡Levi-Civita Symbols
💡Permutation Symbols
💡Volume Element
💡Jacobian Factor
💡Absolute Tensors
💡Skew Symmetry
💡Covariant Derivative
💡Metronomic Property
💡Delta Function
Highlights
Introduction of Levi-Civita symbols as new tensor calculus objects.
Explanation of why permutation symbols are relative tensors due to orientation-dependent factors.
Combining forms to create absolute tensors, eliminating orientation-dependent factors.
Definition of Levi-Civita symbols as factors in tensor equations representing absolute tensors under orientation preserving transformations.
Demonstration of the skew symmetry of Levi-Civita symbols with respect to their indices.
Expression of the Kronecker delta function using the product of two Levi-Civita symbols.
Proof that the product of Levi-Civita symbols results in a tensor, confirming the tensorial nature of the delta function.
Capability to raise and lower indices of Levi-Civita symbols using the covariant metric tensor.
Derivation of the covariant derivative of Levi-Civita symbols with lower indexes.
Introduction of a new object t-i-r-s-t to simplify the expression of covariant derivatives.
Analysis of the anti-symmetry properties of t-i-r-s-t with respect to its indices.
General result for t-i-r-s-t, showing its dependence on the permutation of indices and the Christoffel symbols.
Metronomic property of Levi-Civita symbols with lower indexes, where their covariant derivative equals zero.
Application of the covariant derivative to the product of two Levi-Civita symbols, leading to the conclusion of their metronomic property.
Confirmation that both upper and lower indexed Levi-Civita symbols are metronomic objects.
Summary of the properties and significance of Levi-Civita symbols in tensor calculus.
Anticipation of future applications of Levi-Civita symbols in defining additional tensor calculus operations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: