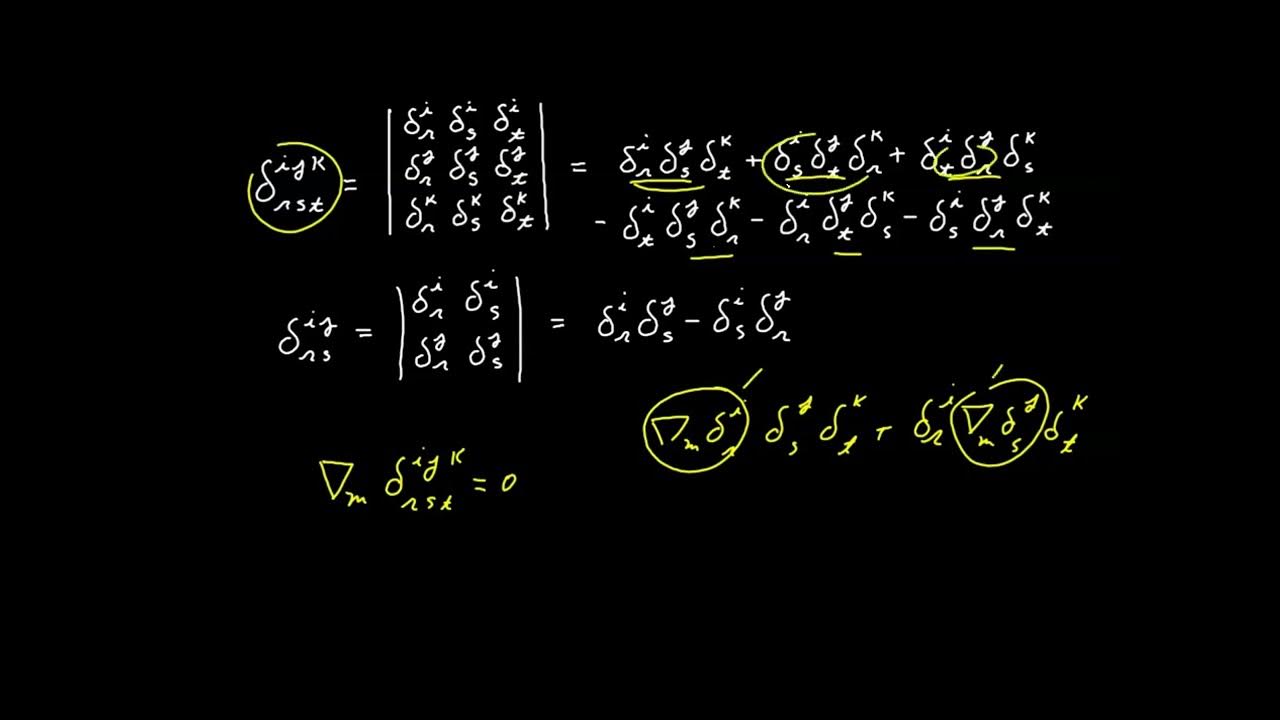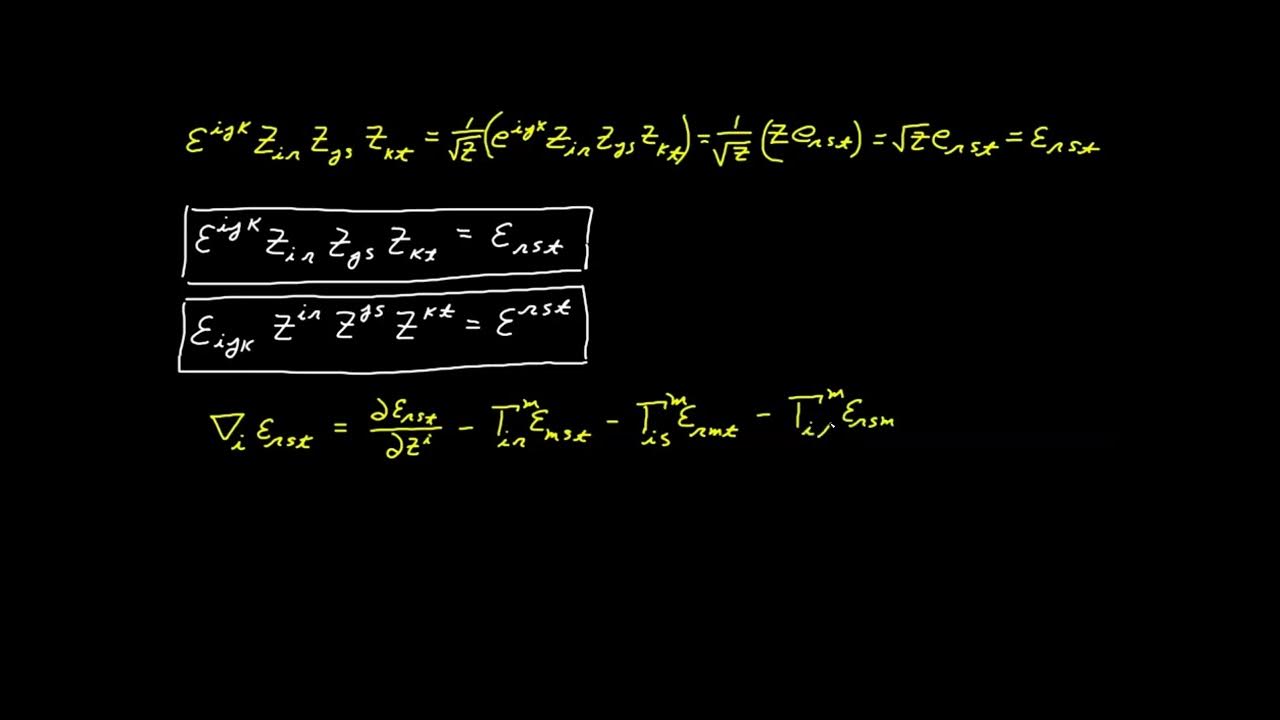Video 55 - Generalization to Other Dimensions
TLDRThis video explores the generalization of tensor calculus concepts beyond three-dimensional space, highlighting the adaptability of expressions to any number of dimensions. It revisits determinants, permutation symbols, and the Delta system, showing modifications for 2D and 4D systems. The script also delves into the extension of the cross product to other dimensions, emphasizing its anti-symmetry and orthogonality properties. The video concludes with the application of physical integrals across dimensions, maintaining the essence of tensor calculus for a broader mathematical understanding.
Takeaways
- 📚 Tensor calculus concepts are generalizable to any number of dimensions, not just three.
- 🔍 When dealing with determinants in dimensions other than three, expressions need to be modified to accommodate the different number of indices.
- 🔄 The concept of total symmetry and anti-symmetry in tensor components applies across all dimensions, affecting the degrees of freedom.
- 📏 The permutation symbol and its rules remain consistent in all dimensions, with the only change being the number of indices used.
- 📉 The determinant expressions for two, three, and four dimensions illustrate the need to adjust the number of factors and the factorial in the denominator.
- 🔢 The Delta function and its properties, including its determinant-based definition, extend naturally to two and four dimensions.
- 📐 The properties of the Jacobian and its determinant do not change with dimensionality, maintaining consistent weights across different systems.
- 📝 Cofactor expressions vary with the number of factors and indices, always matching the number of dimensions, but the inverse relationships remain the same.
- 📦 The volume element expressions are universal across different dimensions, with adjustments needed only for elements involving permutation symbols or the Delta system.
- 🌀 The concept of the cross product can be extended to other dimensions, although it is traditionally associated with three dimensions.
- 🤔 The magnitude of the cross product in two dimensions is equal to the magnitude of the original vector, a unique property not seen in three or four dimensions.
Q & A
What is the main strength of tensor calculus mentioned in the video?
-The main strength of tensor calculus is its generalizability. The expressions developed in tensor calculus are usually applicable to systems of any number of dimensions.
Why do expressions involving determinants need to be modified when working with systems other than three dimensions?
-Expressions involving determinants need to be modified for systems other than three dimensions because they involve a different number of factors and indexes, which must align with the dimensionality of the system being worked with.
How does the number of degrees of freedom change with different dimensions in the context of totally symmetric and anti-symmetric systems?
-In totally symmetric systems, the number of degrees of freedom is reduced due to the symmetry, while in totally anti-symmetric systems, there is always only one degree of freedom, regardless of the number of dimensions.
What are the rules for using permutation symbols in any number of dimensions?
-The rules for using permutation symbols are the same in any number of dimensions: if there are duplicates in the index values, the permutation symbol is zero; if it's an even permutation of unique values, it's positive one; if it's an odd permutation, it's negative one.
How does the expression for a determinant change when moving from a three-dimensional system to a two or four-dimensional system?
-The expression for a determinant changes by adjusting the number of factors and the number of indexes in the permutation symbol to match the dimensionality of the system, i.e., using two factors for a 2x2 determinant and four factors for a 4x4 determinant.
What is the significance of the Delta system in extending determinant expressions to different dimensions?
-The Delta system is significant because it allows for the expression of determinant values in a way that can be easily extended to different dimensions by using matrices of the corresponding dimension (2x2 for two dimensions, 4x4 for four dimensions, etc.).
How does the concept of the Jacobian matrix and its determinant change when moving between different dimensions?
-The concept of the Jacobian matrix and its determinant changes by adjusting the number of factors and indexes to match the dimensionality of the system. The weights associated with the determinant remain the same, but the number of factors and indexes changes accordingly.
What is the relationship between the number of terms in the contraction of a determinant and the dimensionality of the system?
-The number of terms in the contraction of a determinant is equal to the factorial of the number of unique indexes, which corresponds to the dimensionality of the system (e.g., 2! for two dimensions, 3! for three dimensions, etc.).
Why are the expressions for the volume element consistent across different dimensions?
-The expressions for the volume element are consistent across different dimensions because they do not involve the permutation symbol or the Delta system, which are the elements that require modification based on dimensionality.
How does the concept of the cross product extend to dimensions other than three?
-The concept of the cross product extends to other dimensions by combining vectors with the Levi-Civita symbol to create a new vector orthogonal to the original vectors. In two dimensions, it involves one vector and the Levi-Civita symbol, while in four dimensions, it involves three vectors and the four-dimensional Levi-Civita symbol.
What is unique about the magnitude of the cross product in two dimensions?
-In two dimensions, the magnitude of the cross product of a vector with itself is equal to the magnitude of the original vector, which is a unique property not seen in three or four dimensions.
Why is the curl operation defined only in three dimensions?
-The curl operation is defined only in three dimensions because it has no practical correspondence or application in two or four dimensions, where attempts to define it result in convoluted expressions without practical use.
How does the concept of a physical integral extend to different dimensions?
-The concept of a physical integral extends to different dimensions by modifying the number of factors in the volume differential, using either a double, triple, or quadruple integration combined with the volume element to ensure an invariant expression for the evaluation of the integral.
Outlines
📚 Generalizing Tensor Calculus to Higher Dimensions
This paragraph introduces the concept of extending the principles of tensor calculus, previously discussed in a three-dimensional context, to spaces with varying dimensions. The video script explains that while tensor calculus expressions are generally applicable to any number of dimensions, certain expressions involving determinants require modification when applied to systems beyond three dimensions. The speaker organizes the content to compare expressions for determinants in two, three, and four dimensions, highlighting the degrees of freedom and the symmetry properties of tensors. The importance of the permutation symbol and its rules in any number of dimensions is also emphasized.
🔍 Delving into Determinants and Delta Systems Across Dimensions
The second paragraph delves deeper into the specifics of determinants, discussing how to express and calculate them in two, three, and four dimensions. It explains the significance of factorials in the explicit definition of determinants and how the Delta system, introduced in a 3x3 matrix context, can be extended to 2x2 and 4x4 matrices. The paragraph also covers the identities involving the Delta system and how they simplify to the value of N when contracted in various dimensions. The concept of relative tensors and Jacobians is touched upon, highlighting the consistency of weights across different dimensional systems.
🔢 Cofactors, Volume Elements, and Tensor Expressions
This paragraph focuses on the concept of cofactors and their relationship with determinants, showing how the formula for cofactors varies with the number of dimensions. It discusses the universality of certain expressions involving determinants and how they remain consistent even when the number of dimensions changes. The discussion then moves to volume elements, explaining how they are represented in different dimensions and the importance of the volume element in integral calculus. The paragraph also mentions the Voss vial formula and its invariant nature across dimensions.
📐 The Versatility of the Cross Product in Various Dimensions
The fourth paragraph challenges the notion that the cross product is exclusive to three dimensions, arguing that the concept can be extended to other dimensions as well. It explains how the cross product is essentially an operation involving one less vector than the dimensionality of the system, creating a new vector orthogonal to the original ones. The paragraph also discusses the anti-symmetry property of the cross product and its implications for orthogonality. Additionally, it touches on the magnitude of the cross product in different dimensions, providing a specific example for two dimensions and suggesting an exercise for four dimensions.
🚫 The Uniqueness of the Curl and Physical Integrals Across Dimensions
The final paragraph addresses the limitations of the curl operation, which is unique to three dimensions and does not have a practical application in other dimensions. It then discusses the concept of physical integrals and how they can be extended to higher dimensions by adjusting the volume differential and using multiple integrations. The paragraph emphasizes the importance of using the volume element to ensure the invariance of the physical integral expression. The video script concludes with a summary of the information covered and a preview of the next video's content.
Mindmap
Keywords
💡Tensor Calculus
💡Determinants
💡Dimensions
💡Symmetry
💡Degrees of Freedom
💡Permutation Symbol
💡Delta System
💡Jacobian
💡Cofactor
💡Volume Element
💡Voss vial Formula
💡Levi-Civita Symbol
💡Cross Product
💡Curl
💡Physical Integral
Highlights
Tensor calculus concepts can be generalized to any number of dimensions.
Expressions developed in tensor calculus are usually applicable to systems of any dimensions.
Determinants require modification when working with systems other than three dimensions.
Totally symmetric systems have 10 degrees of freedom, while totally anti-symmetric systems have only one.
Permutation symbols can be used in any number of dimensions with modified index counts.
The rules for using permutation symbols remain consistent across different dimensions.
Determinant expressions need to be adjusted based on the number of factors and indexes.
The Delta system can be extended to two and four dimensions using 2x2 and 4x4 matrices, respectively.
The contraction of the Delta system yields the value of N, which steps downward with increased dimensions.
Jacobian determinants require a change in the number of factors when moving between dimensions.
The weights in relative tensors do not change between different dimensional systems.
Cofactors formula varies with the number of factors and indexes, matching the dimensions of the system.
The inverse relationships for determinants remain the same across different systems.
Volume elements expressions are universal and do not require modification between dimensions.
The Voss vial formula maintains the same form in all systems, with the only change being the number of terms due to contraction.
The Levi-Civita symbol is defined similarly in all dimensions, with the number of indexes matching the system's dimensionality.
Cross product concepts can be extended to other dimensions, despite not being expressible as a dyadic form outside three dimensions.
The cross product is not commutative, and the order of vector factors affects the sign of the result.
The magnitude of the cross product in two dimensions is equal to the magnitude of one of the original vectors.
Curl is defined only in three dimensions and remains undefined in other spaces.
Physical integrals can be extended to other dimensions by modifying the volume differential and using appropriate integration methods.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: