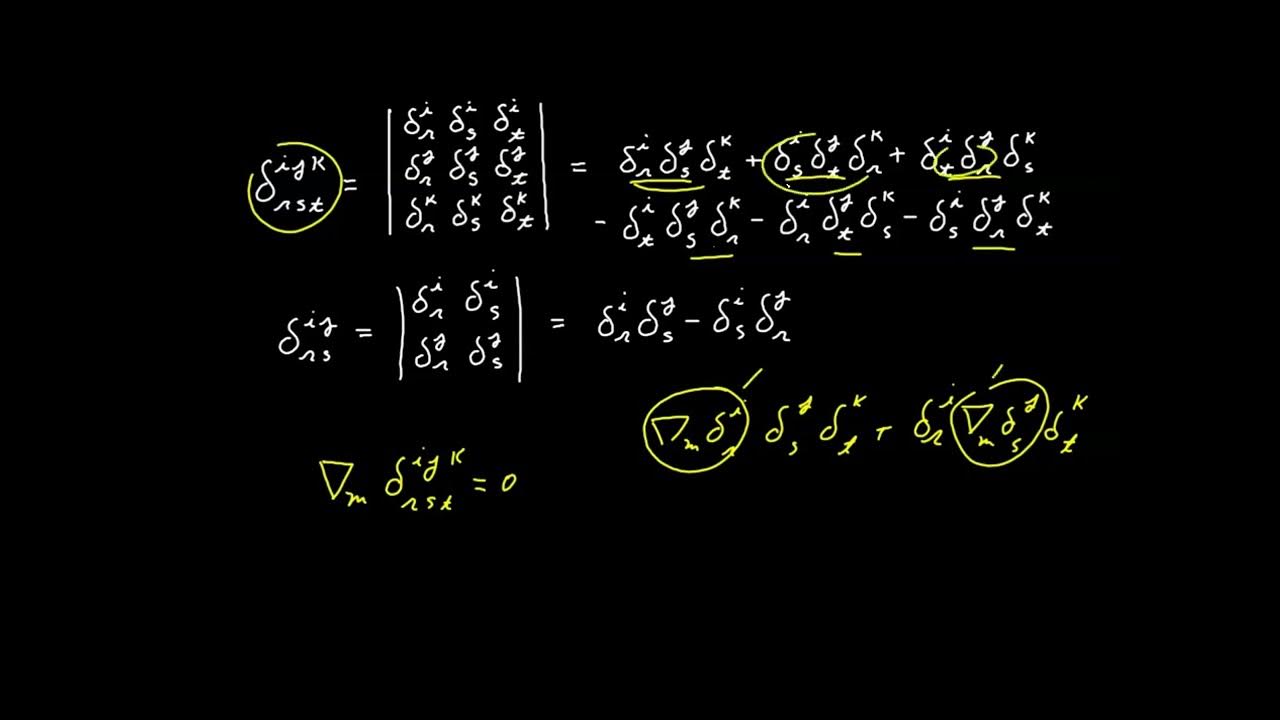Einstein Notation: Proofs, Examples, and Kronecker Delta
TLDRThis video script delves into Einstein notation, explaining how to identify free and dummy indices using bracket operations. It clarifies the process with step-by-step examples and distinguishes between non-identities and identities in tensor expressions. The script also introduces the Kronecker Delta symbol, demonstrating its role in simplifying tensor calculus by eliminating off-diagonal terms. The explanation is aimed at solidifying understanding through practice and proofs, making complex concepts more accessible.
Takeaways
- 📚 Einstein notation uses indices to represent quantities in tensor calculus, with brackets indicating summation over repeated indices.
- 🔍 To determine free and dummy indices, combine terms inside and outside brackets separately to understand index occurrences, then identify the largest count of each index.
- 🔑 Free indices occur only once in the entire expression, while dummy indices occur more than once and are summed over.
- 📈 The video explains three major non-identities in Einstein notation, highlighting inconsistencies in index occurrences and summation properties.
- 📉 The first non-identity shows inconsistency between the left and right sides of an equation due to different index occurrences.
- 📊 The second non-identity points out that swapping indices can lead to different coefficients, indicating the sides of an equation are not necessarily equal.
- 📝 The third non-identity emphasizes that terms with different indices cannot be combined under the summation convention without proper justification.
- 🔄 The video also covers five identities in Einstein notation, explaining why they hold true based on consistent index occurrences and commutative properties of multiplication.
- 📐 The fourth identity is proven by summing over dummy indices and showing that it simplifies to twice the product of the tensor and its components.
- 📈 The fifth identity demonstrates that adding tensors with swapped indices and subtracting the original tensor results in zero, proving tensor equality.
- 🎯 The Kronecker Delta symbol is introduced as a tool to eliminate off-diagonal terms in tensor expressions, defined as 1 when indices are equal and 0 otherwise.
Q & A
What is Einstein notation and how does it relate to indices in mathematical expressions?
-Einstein notation, also known as Einstein summation convention, is a notational convention used in mathematics and physics, particularly in tensor calculus, where an implied summation is assumed over any index variable that appears twice in a single term, once as a subscript and once as a superscript.
How do you determine the free and dummy indices in an expression with Einstein notation?
-To determine free and dummy indices, first combine the terms inside the parentheses with the term outside for the purpose of index analysis, not for multiplication. Then, identify the largest count of each index from the breakdown. An index is considered dummy if it occurs the largest number of times in any combination, while a free index occurs less frequently.
What are the three major non-identities mentioned in the script, and why are they non-identities?
-The three major non-identities are expressions that do not hold true due to inconsistencies in index summation or ordering. They are: 1) a_ik * x_j + a_jk * x_i ≠ a_jk * x_i + a_ik * x_j, 2) a_ij * a_ji ≠ a_ji * a_ij, and 3) a_ij * x_i * y_j + a_ji * x_j * y_i ≠ 2 * a_ij * x_i * y_j. These are non-identities because the indices do not consistently sum over the same range or the terms are not necessarily equal due to the commutative property not applying in all cases.
Can you provide an example of how to apply Einstein notation to simplify an expression with brackets?
-Certainly. Consider the expression a_ij * (b_i * c_j + d_k). First, combine a_ij with each term inside the parentheses to determine the indices' roles. Then, count the occurrences of each index to determine if they are free or dummy. In this case, both i and j would likely be dummy indices if they occur more than once in the combinations, while k would be a free index if it occurs only once.
What is the significance of the Kronecker Delta symbol in tensor calculus?
-The Kronecker Delta symbol, denoted as δ_ij, is a useful tool in tensor calculus that equals 1 when the indices i and j are equal and 0 otherwise. It effectively eliminates off-diagonal terms in matrices or tensors, simplifying expressions where only diagonal elements are considered.
How does the Kronecker Delta symbol simplify expressions involving tensors?
-When the Kronecker Delta is multiplied by tensor components, it effectively picks out the diagonal components of the tensor. For example, δ_ij * x_i * x_j simplifies to x_i^2 when i and j are equal, and 0 otherwise, because the Kronecker Delta is zero when i ≠ j.
What are the five identities mentioned in the script, and how do they relate to Einstein notation?
-The five identities are expressions that hold true under Einstein notation due to the properties of index summation and the commutative property of multiplication. They are: 1) a_ik * x_j + a_jk * x_i = a_jk * x_i + a_ik * x_j, 2) a_ij * x_i * y_j = a_ji * x_j * y_i, 3) a_ij * x_j * x_i = a_ji * x_i * x_j, 4) a_ij * x_i * x_j + a_ji * x_j * x_i = 2 * a_ij * x_i * x_j, and 5) a_ij * x_i * x_j - a_ji * x_j * x_i = 0.
Can you explain why the first identity holds true under Einstein notation?
-The first identity holds true because the indices on both sides of the equation are consistent. On the left side, i is a free index and j is a dummy index, and the same is true for each term on the right side. Since the indices are summed over the same range, the two sides are equivalent.
How does the commutative property of multiplication relate to the second identity in Einstein notation?
-The second identity, a_ij * x_i * y_j = a_ji * x_j * y_i, holds true due to the commutative property of multiplication, which states that the order of multiplication does not affect the result. Since i and j are dummy indices, their order can be switched without changing the outcome.
What is the proof for the fourth identity in Einstein notation, and why does it hold true?
-The fourth identity, a_ij * x_i * x_j + a_ji * x_j * x_i = 2 * a_ij * x_i * x_j, holds true because when you expand the left side using the Einstein summation convention, the diagonal terms (where i = j) are counted twice, and the non-diagonal terms cancel out due to the commutative property, leaving you with twice the sum of the diagonal terms, which is the right side of the identity.
What is the proof for the fifth identity in Einstein notation, and why does it result in zero?
-The fifth identity, a_ij * x_i * x_j - a_ji * x_j * x_i = 0, results in zero because when you expand the left side, the diagonal terms cancel out (since they are the same), and the non-diagonal terms also cancel out due to the subtraction and the commutative property, leading to a sum of zero.
Outlines
📚 Understanding Einstein Notation and Indices
This paragraph delves into the intricacies of Einstein notation, particularly the concept of free and dummy indices within bracketed expressions. The explanation begins with a step-by-step guide on how to identify these indices, emphasizing the importance of not assuming distributive properties. It then illustrates the process with a specific example, highlighting how to combine terms to determine index counts. The paragraph further clarifies the distinction between free and dummy indices by analyzing the largest index counts. The speaker also introduces three major non-identities in Einstein notation, providing explanations rather than rigorous proofs, to demonstrate why certain expressions do not hold true due to index inconsistencies. The summary encourages practice and proofs to solidify understanding.
🔍 Exploring Non-Identities and Kronecker Delta in Einstein Notation
The second paragraph continues the discussion on Einstein notation, focusing on non-identities and the Kronecker Delta symbol. It starts by examining why certain expressions are non-identities, using index analysis to show inconsistency between equation sides. The speaker then presents five identities in Einstein notation, explaining their validity without full proofs. A detailed proof is provided for the fourth identity, demonstrating how it simplifies to the right-hand side using summation and the properties of dummy indices. The fifth identity is briefly mentioned, with a note on its proof method being similar to the fourth. The paragraph concludes with an introduction to the Kronecker Delta symbol, defining its use in eliminating off-diagonal terms in tensor calculus and showing its application in simplifying expressions. An example is given to illustrate the simplification process using the Kronecker Delta.
Mindmap
Keywords
💡Einstein Notation
💡Free Index
💡Dummy Index
💡Tensor
💡Non-Identity
💡Identity
💡Kronecker Delta
💡Commutative Property
💡Summation Convention
💡Distributive Property
💡Coefficient
Highlights
Explanation of how to determine free and dummy indices in Einstein notation when dealing with terms in brackets.
Process of combining terms outside and inside parentheses separately to determine index meanings in Einstein notation.
Importance of not assuming distributive properties in Einstein notation during index analysis.
Method to combine the largest count of each index to determine if an index is free or dummy.
Clarification on the difference between free and dummy indices in the context of Einstein notation.
Introduction to three major non-identities in Einstein's notation with explanations.
Analysis of why certain combinations of indices result in non-identities due to inconsistency.
Demonstration of how to prove non-identities by expanding terms and comparing coefficients.
Discussion on the commutative property of multiplication and its relation to Einstein notation identities.
Explanation of how to use the Kronecker Delta symbol to eliminate off-diagonal terms in tensor calculus.
Definition and properties of the Kronecker Delta symbol in the context of Einstein notation.
Example of simplifying expressions using the Kronecker Delta symbol to isolate diagonal terms.
Introduction to five identities in Einstein notation and their significance in tensor calculus.
Explanation of why certain identities hold true based on the consistency of indices on both sides of an equation.
Proof of the fourth identity in Einstein notation using summation and simplification techniques.
Proof of the fifth identity demonstrating the cancellation of terms leading to an outcome of zero.
Application of Einstein notation in practice with examples and proofs to solidify understanding.
Acknowledgment of patrons supporting the educational content on Einstein notation and tensor calculus.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: