What happens if we DON'T ignore Air Resistance

ZPhysics

27 Jun 202327:31

EducationalLearning

32 Likes 10 Comments

TLDRIn this complex physics exploration, the video delves into the challenging problem of calculating the range of a projectile with air resistance. The script starts with a simplified approach, then transitions to a detailed analysis involving differential equations and integration techniques. It introduces concepts like resistive force proportional to velocity, and the impact of air resistance on the motion. The presenter guides through solving differential equations for both the x and y components of the projectile's motion, ultimately revealing the limitations on range due to air resistance, making it a stimulating journey for those interested in advanced physics.

Takeaways

📚 The script discusses the complexity of calculating the range of a projectile when air resistance is taken into account.
🔍 Initially, the range of a projectile is calculated without considering air resistance, assuming horizontal speed is constant.
🌪️ The introduction of air resistance significantly complicates the problem, as it requires considering a resistive force proportional to the speed.
📉 The script explains that air resistance is often simplified to be proportional to the velocity (V), but in reality, it can be more complex, often proportional to V^2.
🧩 The problem is broken down into horizontal and vertical components, each requiring a separate differential equation to solve.
🔄 The horizontal motion is modeled by a second-order differential equation considering the drag force, leading to an integration involving exponential functions.
📉 For the vertical motion, the script derives a differential equation that includes both the drag force and gravitational force, resulting in a more complex integration.
✍️ The script uses integrating factors to solve the differential equations, which is a technique for solving first-order linear differential equations.
🔢 Boundary conditions, such as initial velocity and starting position, are applied to determine the constants of integration in the derived equations.
📈 The final expressions for the x and y coordinates of the projectile are obtained, which are dependent on time and incorporate the effects of air resistance.
🚫 The script concludes that the x-coordinate of the projectile cannot exceed a certain value due to the limitations imposed by the natural logarithm function in the equations.
🎓 The video script is described as a university-level problem, indicating the advanced nature of the physics concepts discussed.

Q & A

What is the main topic discussed in the video script?
-The main topic discussed in the video script is the calculation of the range of a projectile motion with air resistance included.
Why is the calculation of projectile motion with air resistance more complicated than without it?
-The calculation is more complicated because air resistance introduces a resistive force that is proportional to the speed of the projectile, which requires solving a set of differential equations with non-constant coefficients.
What is the role of the horizontal speed in the projectile motion without air resistance?
-In the absence of air resistance, the horizontal speed is constant because there are no forces acting in the horizontal direction, and it is used to calculate the range of the projectile.
What is the differential equation for the x-direction in the presence of air resistance?
-The differential equation for the x-direction with air resistance is \( x'' + \gamma x' = 0 \), where \( x'' \) is the second derivative of x with respect to time, \( x' \) is the first derivative, and \( \gamma \) is a constant related to air resistance.
What technique is used to solve the differential equation for the x-direction?
-The technique used to solve the differential equation for the x-direction is multiplying by an integrating factor, which is \( e^{\gamma t} \), and then integrating both sides of the equation.
What boundary conditions are used to determine the constants in the solution for the x-coordinate?
-The boundary conditions used are that the initial speed is U in the x-direction and the initial starting position is at the origin (0,0).
How does the differential equation for the y-direction differ from the x-direction?
-The differential equation for the y-direction includes both the resistive force proportional to the speed and the gravitational force, resulting in \( y'' + \gamma y' = -g \), where \( g \) is the acceleration due to gravity.
What is the significance of the natural log function in the equation for the y-coordinate?
-The natural log function is used to eliminate time from the equation and express the y-coordinate in terms of the x-coordinate, which helps in understanding the relationship between the horizontal and vertical displacements.
What limitation is revealed by the analysis of the natural log function in the context of the projectile motion?
-The analysis reveals that the x-coordinate cannot reach a value greater than \( \frac{U^2}{\gamma} \), because beyond this point, the natural log function would become negative, leading to an undefined situation.
What conclusion can be drawn from the script about the effect of air resistance on the range of a projectile?
-The conclusion is that air resistance significantly reduces the range of a projectile compared to the case without air resistance, as it causes the projectile to lose horizontal speed and fall more quickly.

Outlines

00:00

🚀 Introduction to Projectile Motion and Air Resistance

In this segment, the discussion begins with an introduction to projectile motion, focusing on finding the range of a projectile. The speaker highlights the difference between ideal conditions without air resistance and real-world scenarios where air resistance plays a crucial role. The complexity of incorporating air resistance into the calculations is emphasized, setting the stage for a deeper dive into the physics involved.

05:01

📐 Differential Equations and Air Resistance in X Direction

Here, the speaker explains the differential equation governing the motion in the X direction under the influence of air resistance. The equation is simplified using the concept of integrating factors, and the speaker walks through the steps of solving the equation, highlighting the application of the product rule. The importance of boundary conditions is also mentioned, as they are used to determine constants within the equation.

10:03

🔄 Solving for Constants in the X Direction Equation

This part focuses on solving for the constants in the X direction motion equation using initial conditions, such as the initial speed and position. The speaker systematically differentiates and substitutes the values, leading to the final expression for the X coordinate. This solution paves the way for a similar approach to the more complex Y direction.

15:04

🌍 Tackling the Y Direction: Gravity and Air Resistance

The discussion now shifts to the Y direction, where both gravity and air resistance are considered. The speaker derives the differential equation for Y, which is more complex due to the gravitational component. The same method of integrating factors is applied, and the process of solving the equation is described in detail, including the handling of tricky integrals using integration by parts.

20:06

📊 Finalizing the Y Direction Equation with Boundary Conditions

In this segment, the speaker determines the constants in the Y direction equation using boundary conditions, such as the initial velocity and position. After integrating and simplifying, the final expression for the Y coordinate is obtained. The speaker carefully cancels out terms and explains how the constants are related to the physical parameters of the problem.

25:10

🔗 Combining X and Y Equations to Analyze Projectile Motion

The final part of the discussion involves combining the X and Y equations to eliminate time and analyze the overall projectile motion. The speaker explains the implications of the derived equations, particularly how the X coordinate cannot exceed a certain value due to air resistance. The video concludes with an invitation to explore simpler projectile motion problems, encouraging viewers to apply what they have learned.

Mindmap

Keywords

💡Projectile Motion

Projectile motion refers to the motion of an object that is thrown or projected into the air and is subject to the force of gravity. In the video, the speaker discusses finding the range of a projectile, emphasizing how the horizontal speed remains constant in the absence of air resistance and how the vertical motion is influenced by gravity.

💡Air Resistance

Air resistance is a force that opposes the motion of an object through the air. It is a critical factor in real-world projectile motion, complicating the calculations compared to a vacuum. The video script highlights the difference between theoretical calculations without air resistance and the more complex reality where air resistance must be considered.

💡Differential Equation

A differential equation is a mathematical equation that relates a function with its derivatives, describing how the function changes. The video discusses solving differential equations to model the motion of a projectile with air resistance, explaining the process of integrating and applying boundary conditions to find the solution.

💡Horizontal Speed

Horizontal speed refers to the constant velocity component of a projectile's motion in the absence of forces like air resistance. In the script, the speaker mentions that the horizontal speed is unaffected by gravity and remains constant, which simplifies the calculation of the projectile's range.

💡Gravitational Force

Gravitational force is the force that attracts any object with mass towards the center of the Earth. This force affects the vertical motion of a projectile, pulling it downward. The script explains how gravity is accounted for in the differential equations used to model the projectile's vertical motion.

💡Boundary Conditions

Boundary conditions are specific values or constraints used to solve differential equations, often related to the initial or final state of the system. In the video, boundary conditions such as the initial speed and starting position of the projectile are used to determine the constants in the equations for both horizontal and vertical motion.

💡Integration by Parts

Integration by parts is a mathematical technique used to integrate products of functions. The video demonstrates the use of this technique to solve an integral that arises in the process of finding the range of the projectile, particularly in the context of air resistance affecting the motion.

💡Natural Logarithm (ln)

The natural logarithm is a mathematical function that is the inverse of the exponential function. In the script, the natural logarithm is used to solve an equation involving time, which is then substituted back into the equation for the projectile's vertical motion to eliminate time from the final expression.

💡Exponential Function

An exponential function is a mathematical function of the form e^x, where e is a constant approximately equal to 2.71828. In the video, the exponential function is used in the context of air resistance, where the speed of the projectile is described by an equation involving an exponential decay factor due to air resistance.

💡Product Rule

The product rule is a rule in calculus used to differentiate the product of two functions. The script explains how the product rule is used to solve the differential equations for projectile motion by recognizing a pattern in the form of the equation and applying it to simplify the integration process.

Highlights

Introduction to the complex problem of calculating projectile range with air resistance.

Explanation of why horizontal speed remains constant without air resistance.

Discussion on the complications introduced by air resistance in projectile motion calculations.

Introduction of resistive force proportional to speed in the equation of motion.

Assumption of air resistance being proportional to velocity for simplification.

Derivation of differential equations for projectile motion with air resistance.

Use of integrating factors to solve differential equations in projectile motion.

Explanation of the product rule and its application in solving differential equations.

Integration of differential equations to find expressions for x and y coordinates.

Determination of constants using boundary conditions for the projectile's initial state.

Derivation of the x-coordinate expression with air resistance.

Derivation of the y-coordinate expression with air resistance and its complexity.

Application of integration by parts to solve a complex integral in the y-coordinate equation.

Simplification of the y-coordinate expression to find a general solution.

Analysis of the limitations of the x-coordinate due to the natural log function.

Final expression for the y-coordinate as a function of time with air resistance.

Discussion on the implications of the derived equations for real-world projectile motion.

Encouragement for viewers to explore further physics problems for a deeper understanding.

Transcripts

Browse More Related Video

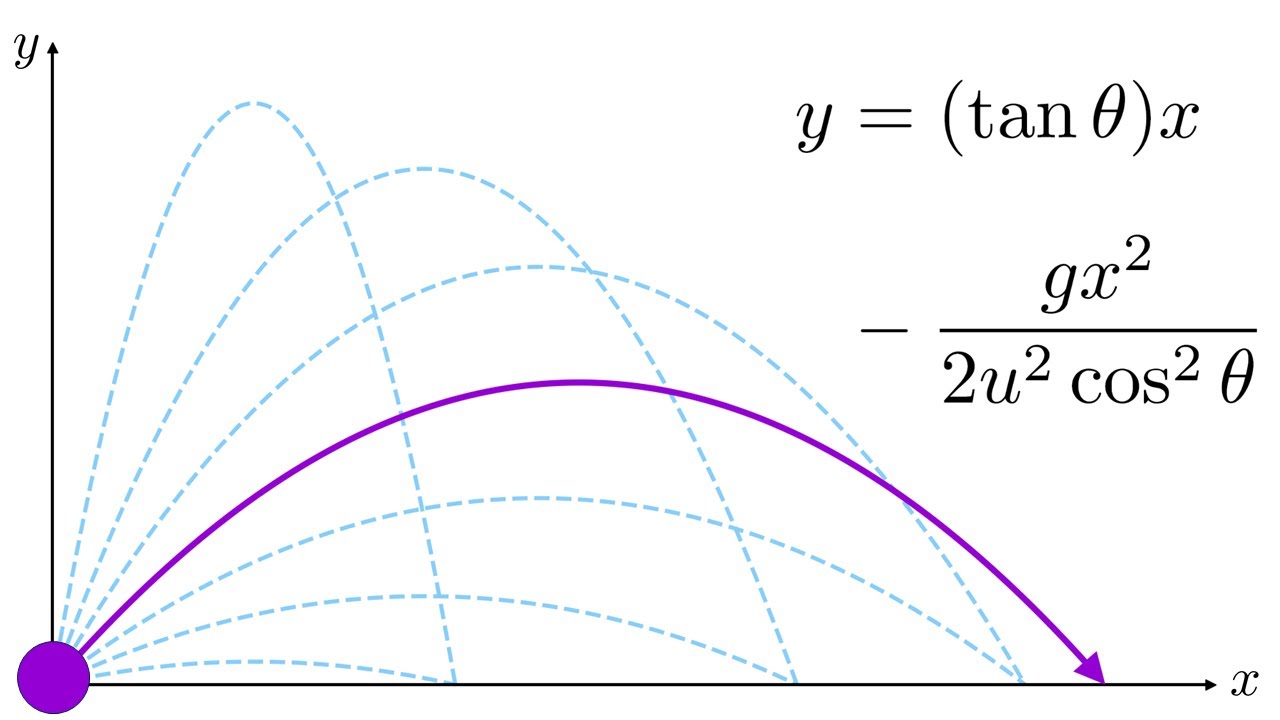
Trajectory of a projectile without drag

Projectile at an angle | Two-dimensional motion | Physics | Khan Academy

2021 Live Review 8 | AP Physics C: Mechanics | Understanding Resistive Forces

Physics 3.5.4h - Projectile Practice Problem 8

Projectile Motion (of an Object Fired at an Angle) - A Level Physics

Introduction to Projectile Motion

Related Tags

Projectile Motion Air Resistance Physics Problem Differential Equations Integration Techniques Motion Analysis Educational Content Advanced Physics Mathematical Modeling Science Education