Introduction to Projectile Motion
TLDRIn this educational video, Mr. P introduces the concept of projectile motion, explaining that it involves an object moving in two dimensions without air resistance. The class learns that in projectile motion, the object is in free-fall in the y-direction with an acceleration of -9.81 m/s^2, while in the x-direction, it moves at a constant velocity since there's no acceleration. The key to solving projectile motion problems is understanding the separate equations of motion for x and y and recognizing that the change in time is a scalar, which can be solved first and applied to both directions.
Takeaways
- 📚 The lesson introduces the concept of projectile motion, which involves an object moving in two dimensions (x and y) without air resistance.
- 🚀 Projectile motion is analyzed by separating the motion into horizontal (x) and vertical (y) components due to different equations of motion in each direction.
- 🎯 In the vertical (y) direction, an object in projectile motion experiences free-fall with an acceleration of -9.81 m/s², which is the acceleration due to gravity on Earth.
- 🌟 The horizontal (x) direction involves constant velocity motion since there is no acceleration; the ball moves at a constant speed in this direction.
- 🔢 To solve projectile motion problems, one must identify known variables in both the x and y directions separately and apply the appropriate equations of motion.
- 🔍 For the y direction, the uniformly accelerated motion (UAM) equations are used, requiring knowledge of three variables to solve the problem.
- 🌐 In the x direction, only two variables are needed to solve the problem, as the motion is at a constant velocity.
- 🕒 The change in time is a scalar quantity, which means it is independent of direction and can be solved for and applied to both the x and y directions.
- 📈 Stop motion photography is mentioned as a technique used to graph the position of a dropped ball as a function of time, illustrating linear motion examples.
- 🤔 The strategy for solving projectile motion problems involves understanding the different motions in each direction and the variables involved in each case.
- 🎓 The lesson emphasizes the importance of knowing the right variables and equations to solve problems involving projectile motion effectively.
Q & A
What is projectile motion?
-Projectile motion refers to the motion of an object that is flying through a vacuum, moving in at least two dimensions, typically the horizontal (x) and vertical (y) directions.
Why is the motion in the x direction considered to be at a constant velocity?
-In projectile motion, there is no acceleration to the left or right because there is no force acting in those directions. Thus, the object moves at a constant velocity in the x direction, which is usually zero if the object is dropped.
What is the acceleration of an object in free-fall?
-An object in free-fall has an acceleration equal to the gravitational acceleration, which is -9.81 meters per second squared (negative because it acts downward).
How many UAM (Uniformly Accelerated Motion) variables are there in total?
-There are five UAM variables: final velocity, initial velocity, acceleration, change in time, and displacement.
How many UAM equations are available for solving problems?
-There are four UAM equations that can be used to solve physics problems involving uniformly accelerated motion.
How many variables do you need to know to solve for the remaining ones in projectile motion?
-You need to know three variables to solve for the remaining two in the y direction and two variables in the x direction to solve for the third one in projectile motion.
Which UAM variable is a scalar?
-The change in time is the scalar variable among the UAM variables. It is independent of direction and can be applied to both the x and y directions.
Why is solving for the change in time important in projectile motion problems?
-The change in time is important because it is a scalar and can be used to solve for other variables in both the x and y directions, making it a crucial factor in analyzing projectile motion.
What is the basic strategy for solving a projectile motion problem?
-The basic strategy for solving a projectile motion problem is to split the known variables into the x and y directions because the equations of motion are different for each direction.
How does the motion of a ball thrown upward compare to that of a ball dropped?
-Both balls experience the same acceleration due to gravity, but they have different initial velocities and thus follow different trajectories. A thrown ball has an initial upward velocity, while a dropped ball starts with zero initial velocity and accelerates downward.
What is the significance of analyzing objects with different masses dropped from the same height?
-Analyzing objects with different masses dropped from the same height helps to understand that in the absence of air resistance, all objects fall at the same rate due to gravity, regardless of their mass.
How does stop motion photography help in studying motion?
-Stop motion photography allows for the detailed analysis of an object's position as a function of time, providing a visual representation of motion that can be graphed and studied frame by frame.
Outlines
📚 Introduction to Projectile Motion
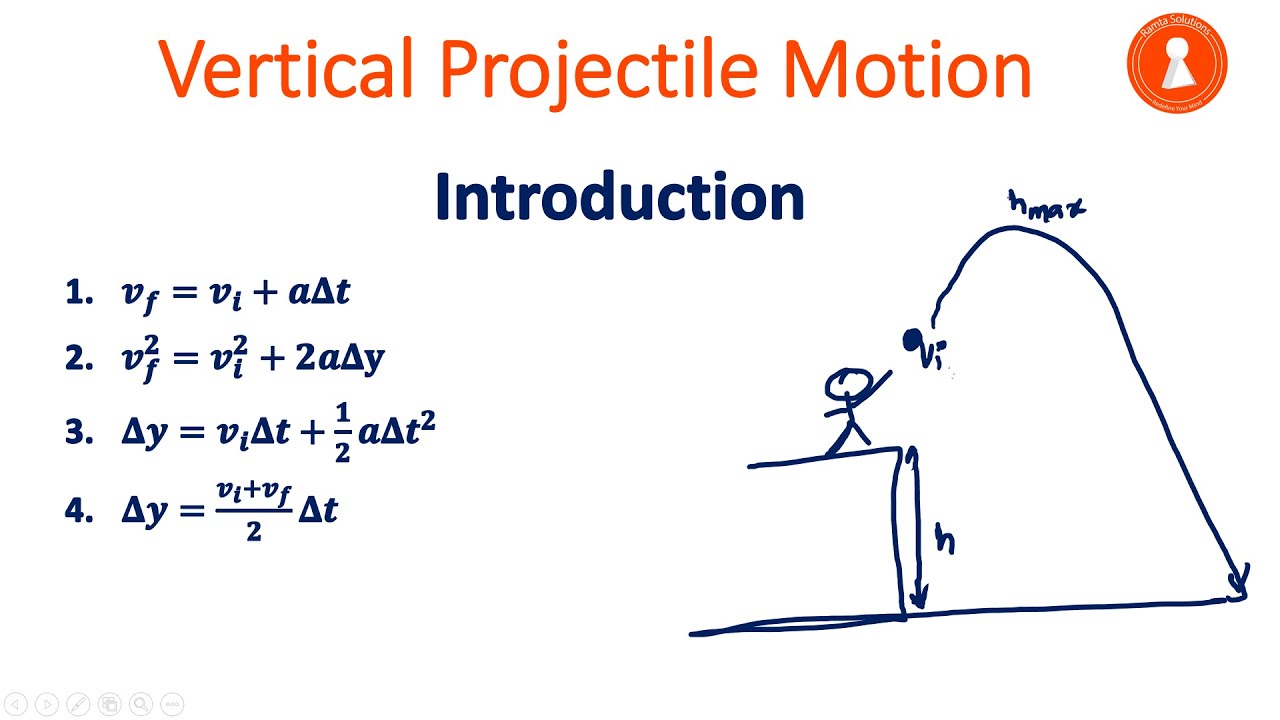
This paragraph introduces the concept of projectile motion, marking a transition from linear motion to a more complex two-dimensional motion. The discussion begins with a recap of previously studied types of motion, such as constant velocity and acceleration (both positive and negative), uniformly accelerated motion, and free-fall acceleration. The introduction of projectile motion is presented with a touch of drama and excitement. The key point emphasized is that in projectile motion, an object moves in two dimensions through a medium, referred to as a vacuum that one can breathe, meaning there is no air resistance. The strategy for solving projectile motion problems is introduced, highlighting the importance of separating the known variables into x and y components due to the different equations of motion in each direction. The paragraph sets the stage for a deeper dive into the physics of projectile motion.
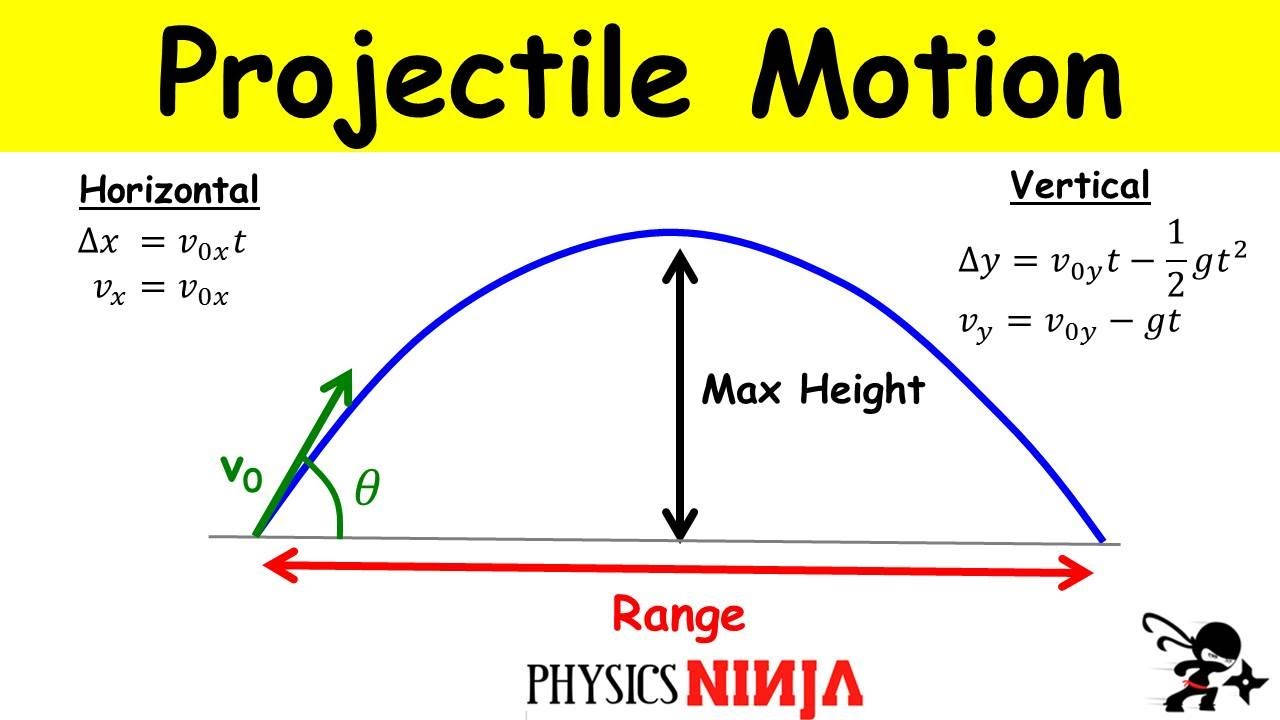
🔍 Analysis of Projectile Motion in X and Y Directions
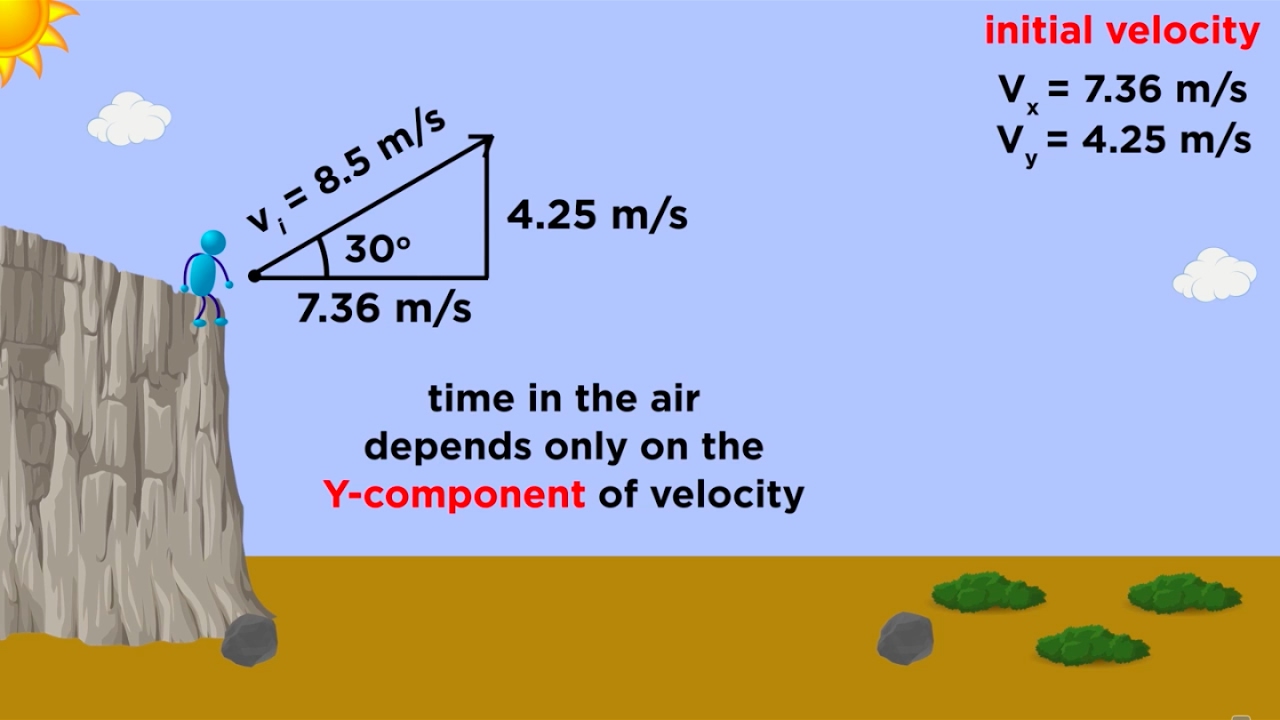
This paragraph delves into the specifics of analyzing projectile motion by examining the separate components of motion in the x and y directions. It is explained that in the y direction, the object is in free-fall with an acceleration of -9.81 m/s^2, allowing the use of uniformly accelerated motion (UAM) equations. The importance of knowing three variables to solve for the remaining two in the y direction is stressed. In contrast, the x direction involves no acceleration, meaning the object moves at a constant velocity, and only two variables are needed to solve equations in this direction. The scalar nature of change in time is highlighted as a crucial factor in solving projectile motion problems, as it can be solved independently and applied to both directions. The summary emphasizes the need to list known variables separately for the x and y directions and use appropriate equations based on the number of known variables to solve projectile motion problems.
Mindmap
Keywords
💡Projectile Motion
💡Uniformly Accelerated Motion (UAM)
💡Free-Fall
💡Acceleration
💡Constant Velocity
💡Equations of Motion
💡Displacement
💡Velocity
💡 Scalars and Vectors
💡Dimension
💡Negative Acceleration
Highlights
Introduction to projectile motion as a type of motion involving movement in two dimensions.
Discussion on the previous analysis of various types of motion including constant velocity and acceleration, both positive and negative.
Explanation of projectile motion occurring in a vacuum, emphasizing the absence of air resistance.
Strategy for solving projectile motion problems by separating known variables into x and y directions due to different equations of motion.
Clarification that projectile motion in this class is limited to two dimensions, x and y.
Description of an object in projectile motion as not touching anything and thus being in free-fall in the y direction.
Identification of the acceleration in the y direction during projectile motion as negative 9.81 meters per second squared.
Use of uniformly accelerated motion (UAM) equations for the y direction in projectile motion problems.
Explanation that in the x direction, an object in projectile motion moves at a constant velocity because there is no acceleration.
Relevance of knowing two variables in the x direction and three in the y direction to solve projectile motion problems.
The change in time being a scalar and its applicability to both directions in projectile motion problems.
Emphasis on the importance of listing known variables separately for the x and y directions when approaching a projectile motion problem.
The y direction's acceleration being equal to negative g (9.81 m/s^2) on Earth, which is a crucial piece of information for solving problems.
In projectile motion, the x direction maintains a constant non-zero value of velocity, assuming an initial horizontal launch.
The process of solving for the change in time as the primary step in solving projectile motion problems and then applying it to the other direction.
The importance of understanding the difference in equations of motion for the x and y directions when dealing with projectile motion.
The practical application of projectile motion concepts, such as in the analysis of a ball thrown upward or dropped.
Use of stop motion photography as a method to graph the position as a function of time for a dropped ball, showcasing a hands-on learning approach.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: