Projectile at an angle | Two-dimensional motion | Physics | Khan Academy
TLDRThe video script explains the physics of a rocket launching a projectile at a velocity of 10 m/s at a 30-degree angle above the horizontal. It details how to calculate the projectile's range by breaking down the velocity into horizontal and vertical components, using trigonometry and the principles of projectile motion. The calculation assumes negligible air resistance and results in a projectile range of approximately 8.83 meters, highlighting the application of mathematical concepts in real-world scenarios.
Takeaways
- 🚀 A rocket is launching a projectile at a velocity of 10 m/s at an angle of 30 degrees above the horizontal.
- 🔄 The velocity of the projectile is broken down into horizontal and vertical components to simplify the problem.
- 📐 The vertical component is calculated using the sine of the launch angle, resulting in 5 m/s.
- 🕒 The time the projectile stays in the air is determined by the vertical component and acceleration due to gravity (g = -9.8 m/s²).
- 🔢 The time in the air is calculated to be approximately 1.02 seconds using the formula: Δt = Δv / g, where Δv is the change in vertical velocity.
- 🏃 The horizontal component of the velocity is determined using the cosine of the launch angle, resulting in 5√3 m/s.
- 📈 The horizontal displacement is found by multiplying the horizontal velocity component by the time in the air, yielding approximately 8.83 meters.
- 🌙 The problem assumes negligible air resistance, simplifying the physics and allowing for the assumption of constant horizontal velocity.
- 📊 Trigonometry plays a crucial role in calculating both the vertical and horizontal components of the projectile's velocity.
- 🛰 The principles of projectile motion can be applied to understand the trajectory and distance of objects launched under similar conditions.
- 🔍 The script provides a step-by-step approach to solving problems involving projectile motion, emphasizing the importance of breaking down complex motions into manageable components.
Q & A
What is the initial velocity of the projectile?
-The initial velocity of the projectile is 10 meters per second.
What is the angle of the launch relative to the horizontal?
-The angle of the launch is 30 degrees upwards from the horizontal.
How is the velocity vector broken down in the problem?
-The velocity vector is broken down into its vertical and horizontal components to simplify the problem.
What is the method used to determine the vertical component of the velocity?
-The vertical component is determined using the sine of the launch angle, which is 30 degrees in this case.
What is the value of the vertical component of the velocity?
-The vertical component of the velocity is 5 meters per second, calculated as 10 meters per second (initial velocity) times the sin of 30 degrees (1/2).
How is the time the projectile stays in the air calculated?
-The time the projectile stays in the air is calculated by dividing the change in vertical velocity by the acceleration due to gravity (-9.8 meters per second squared).
What is the final vertical velocity of the projectile when it returns to the ground?
-The final vertical velocity of the projectile is -5 meters per second, indicating it is moving downward at the same magnitude but in the opposite direction of the initial velocity.
How is the horizontal component of the velocity determined?
-The horizontal component is determined using the cosine of the launch angle, which is 30 degrees in this case.
What is the value of the horizontal component of the velocity?
-The horizontal component of the velocity is 5√3 meters per second, calculated as 10 meters per second (initial velocity) times the cosine of 30 degrees (√3/2).
How is the total horizontal displacement of the projectile calculated?
-The total horizontal displacement is calculated by multiplying the horizontal component of the velocity by the time the projectile is in the air (1.02 seconds).
What is the total horizontal distance the projectile travels?
-The total horizontal distance the projectile travels is approximately 8.83 meters, calculated as 5√3 meters per second times 1.02 seconds.
Why is air resistance considered negligible in this problem?
-Air resistance is considered negligible to simplify the problem and to allow for a more straightforward application of the principles of physics without the added complexity of drag forces.
Outlines
🚀 Rocket Launch and Velocity Vector Analysis
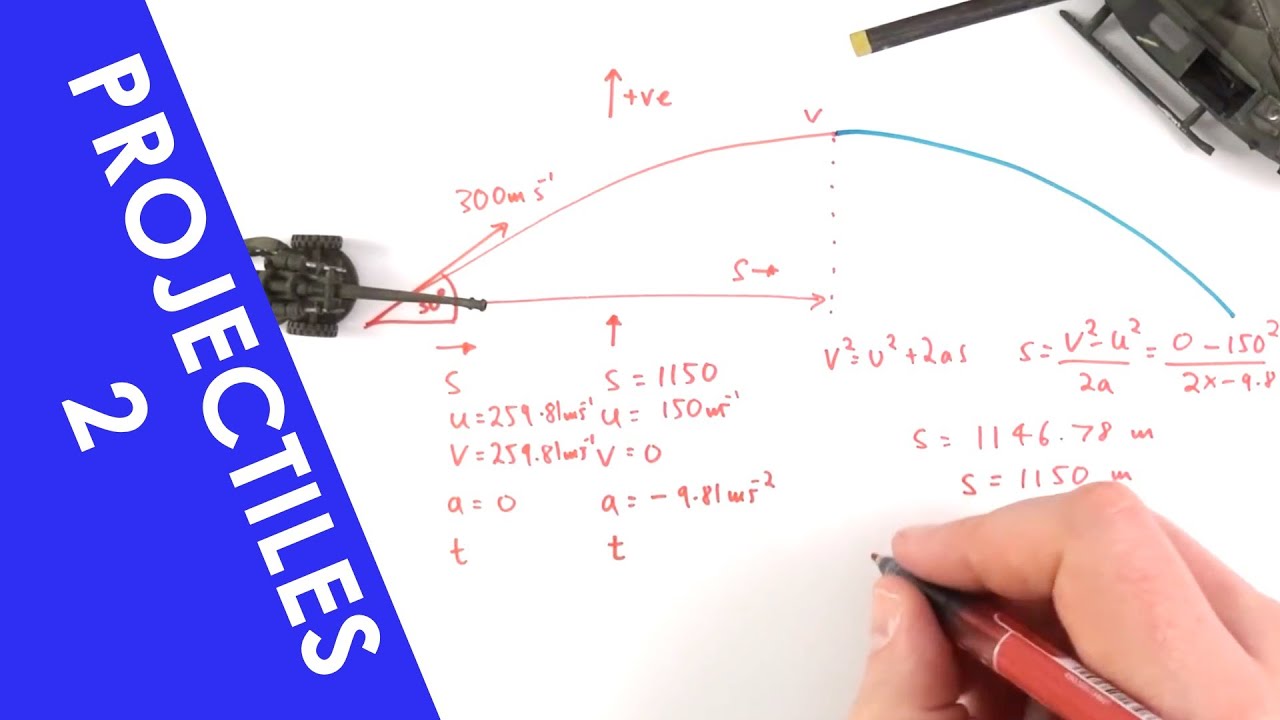
This paragraph introduces the scenario of a rocket launching a projectile at a velocity of 10 meters per second at an angle of 30 degrees above the horizontal. The main focus is on breaking down the velocity vector into its horizontal and vertical components to simplify the problem. The vertical component is used to calculate how long the projectile will be in the air, assuming negligible air resistance. The process involves using trigonometric functions (sine and cosine) to determine the components and apply the principles of physics to predict the projectile's trajectory.
📉 Vertical Motion and Time Calculation
The second paragraph delves into the vertical motion of the projectile, considering the initial and final velocities and the effect of gravity. It explains how to calculate the time the projectile stays in the air using the change in vertical velocity and the acceleration due to gravity (9.8 m/s²). The calculation leads to a result of 1.02 seconds, which is the time the projectile is in the air. This information is crucial for determining the horizontal displacement of the projectile.
🏃♂️ Horizontal Displacement Calculation
The final paragraph focuses on calculating the horizontal displacement of the projectile. It uses the horizontal component of the velocity, found through the cosine of the launch angle (30 degrees), and multiplies it by the time the projectile is in the air (1.02 seconds) to find the total horizontal distance traveled. The horizontal component is determined to be 5√3 meters per second, and when multiplied by the time in the air, the resulting displacement is approximately 8.83 meters.
Mindmap
Keywords
💡Rocket
💡Projectile
💡Velocity
💡Direction
💡Components
💡Trigonometry
💡Gravity
💡Air Resistance
💡Horizontal Component
💡Vertical Component
💡Displacement
Highlights
The rocket launches a projectile with a velocity of 10 meters per second at an angle of 30 degrees above the horizontal.
The problem is simplified by breaking down the velocity vector into its vertical and horizontal components.
The vertical component of the velocity is used to determine how long the rock stays in the air, independent of the horizontal component.
Air resistance is considered negligible in this problem, simplifying the physics of the motion.
The vertical component of the velocity is calculated using the sine of the launch angle, resulting in 5 meters per second.
The time the projectile stays in the air is determined by dividing the change in vertical velocity by the acceleration due to gravity.
The change in vertical velocity is 10 meters per second (from 5 m/s upwards to -5 m/s downwards).
The acceleration due to gravity used in the calculations is -9.8 meters per second squared.
The total time the projectile is in the air is calculated to be approximately 1.02 seconds.
The horizontal component of the velocity is found using the cosine of the launch angle, resulting in 5√3 meters per second.
The horizontal displacement is calculated by multiplying the horizontal velocity component by the time in the air.
The total horizontal displacement of the projectile is approximately 8.83 meters.
This analysis assumes constant horizontal velocity throughout the projectile's flight.
The method used can be applied to a variety of projectile motion problems, regardless of the initial conditions.
The next video will introduce an alternative method for solving the time of flight, applicable to more complex scenarios.
Transcripts
Browse More Related Video
5.0 / 5 (0 votes)
Thanks for rating: