Trajectory of a projectile without drag

Dr Ben Yelverton
6 Oct 202112:26
EducationalLearning
32 Likes 10 Comments

TLDRThis video script delves into the trajectory of a projectile in the absence of air resistance. It begins by establishing a coordinate system and defining the parameters that influence the projectile's path, such as initial speed and launch angle. The script then methodically breaks down the motion into horizontal and vertical components, using parametric equations to describe the x and y coordinates as functions of time. By combining these equations, a Cartesian equation for the trajectory is derived, revealing a parabolic shape. The script further explains how to calculate the range of the projectile, concluding that the maximum range is achieved when the projectile is launched at a 45-degree angle. This comprehensive analysis provides valuable insights into the physics of projectile motion.

Takeaways
  • πŸš€ The video discusses the trajectory of a projectile without considering air resistance.
  • πŸ“ˆ The starting point for the analysis is finding parametric equations for the x and y coordinates as a function of time.
  • πŸ”„ The horizontal motion is analyzed first, assuming no acceleration due to the absence of air resistance.
  • 🏹 The initial velocity vector is decomposed into horizontal (u cos ΞΈ) and vertical (u sin ΞΈ) components.
  • πŸ“Š The horizontal range (x) is described by the equation x = u cos ΞΈ * t, showing a linear relationship with time.
  • πŸ”’ The vertical motion is more complex due to gravity, leading to a quadratic equation for the y coordinate over time.
  • 🌐 The Cartesian equation of the trajectory is derived by eliminating time, resulting in an upside-down quadratic equation (parabola).
  • 🎯 The range (maximum horizontal distance) of the projectile is found by setting y to zero in the Cartesian equation and solving for x.
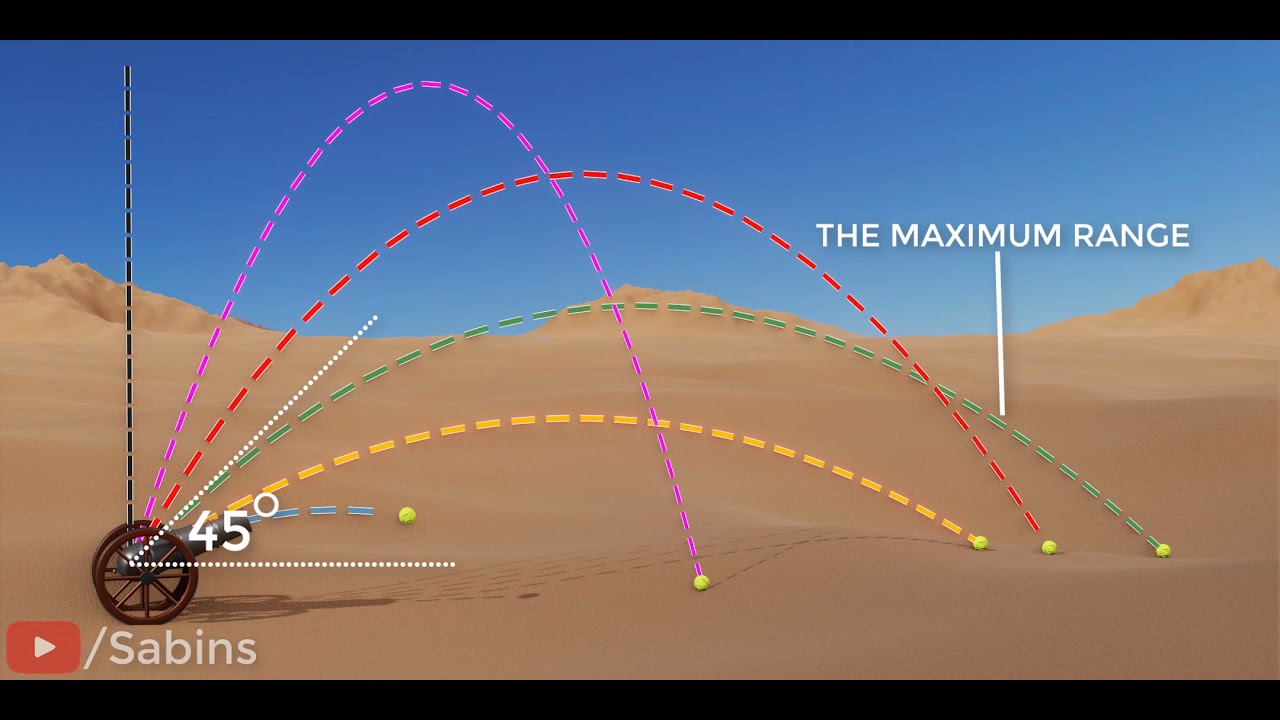
  • πŸ“ˆ The expression for the range is simplified to R = (u^2 * sin(2ΞΈ)) / g, highlighting the dependence on initial speed and launch angle.
  • πŸ“Œ The optimal launch angle for maximum range is determined to be 45 degrees, where sin(2ΞΈ) is maximized.
  • πŸ”œ The video script sets up for a future discussion on the impact of air resistance on projectile motion.
Q & A

  • What is the main topic of the video?

    -The main topic of the video is the trajectory of a projectile, specifically when there is no air resistance involved.

  • What are the two key parameters that determine the shape of the projectile's trajectory?

    -The two key parameters that determine the shape of the projectile's trajectory are the initial speed (u) and the launch angle (theta).

  • How does the coordinate system set up for the analysis?

    -The coordinate system is set up with the origin at the starting point of the projectile, and the y-coordinate increases upwards while the x-coordinate increases to the right.

  • What is the horizontal component of the initial velocity?

    -The horizontal component of the initial velocity is given by u cos(theta), where u is the initial speed and theta is the launch angle.

  • What is the equation for the x-coordinate as a function of time?

    -The equation for the x-coordinate as a function of time is x = u cos(theta) * t.

  • How does gravity affect the vertical motion of the projectile?

    -Gravity affects the vertical motion of the projectile by providing a constant acceleration downwards, which is represented by the acceleration due to gravity (g) in the equations.

  • What is the equation for the y-coordinate as a function of time?

    -The equation for the y-coordinate as a function of time is y = u sin(theta) * t - 0.5 * g * t^2.

  • What is the Cartesian equation of the projectile's trajectory?

    -The Cartesian equation of the projectile's trajectory is y = (tan(theta) * x) - (g * x^2) / (2 * u^2 * cos^2(theta)).

  • How can you find the range of the projectile?

    -To find the range of the projectile, you set y to zero in the Cartesian equation and solve for x, which gives the maximum horizontal distance the projectile travels.

  • What is the optimal launch angle for the maximum range of the projectile?

    -The optimal launch angle for the maximum range of the projectile is 45 degrees, as this is when sine(2*theta) equals one, giving the maximum possible range.

  • What will the video in the follow-up cover?

    -The follow-up video will cover the case where air resistance is present, and how it affects the trajectory and range of the projectile.

Outlines
00:00
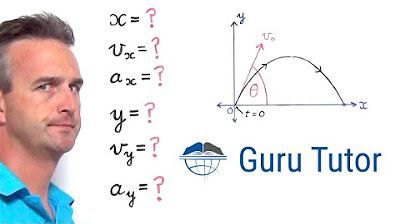
πŸš€ Introduction to Projectile Motion

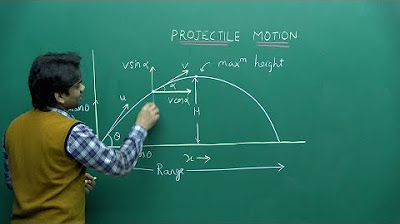
This paragraph introduces the concept of projectile motion, focusing on the trajectory of a projectile without considering air resistance. The video aims to derive parametric equations for the x and y coordinates as functions of time, which will then be combined to find the Cartesian equation of the trajectory. The starting point is defined as the origin of the coordinate system, and the initial velocity vector is described by its length (u) and angle (theta) relative to the horizontal. The importance of initial speed and launch angle in determining the trajectory is highlighted.

05:01
πŸ“ Horizontal and Vertical Components of Motion

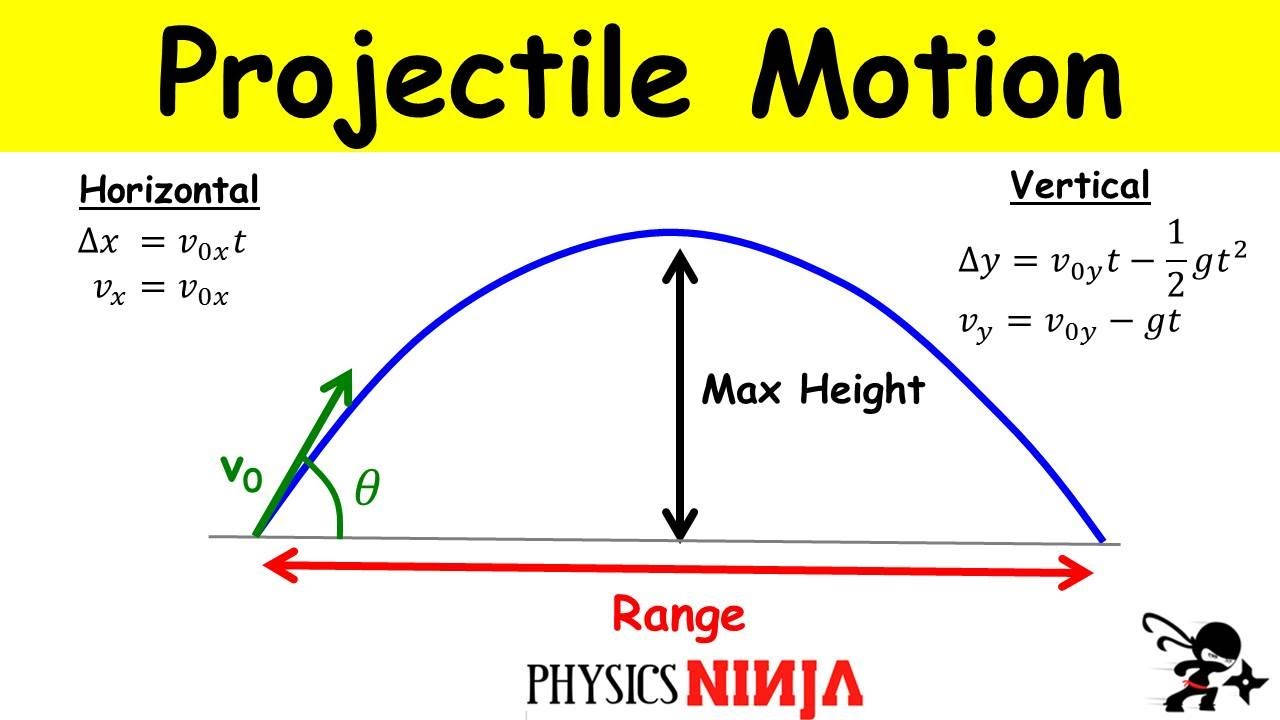
In this paragraph, the analysis of projectile motion is broken down into horizontal and vertical components. The horizontal motion is simpler, with no acceleration and a direct relationship between distance (x) and speed times time (x = u*cos(theta)*t). The vertical motion, however, is influenced by gravity, leading to a constant acceleration (a = -g). The parametric equation for the vertical coordinate (y = u*sin(theta)*t - 0.5*g*t^2) is derived using the constant acceleration (suvat) equations. This sets the foundation for further analysis of the projectile's range and the impact of the launch angle on the trajectory.

10:02
🎯 Calculating the Range of the Projectile

The final paragraph focuses on calculating the range of the projectile, which is the maximum horizontal distance it travels. By setting the y-coordinate to zero (to represent the point where the projectile hits the ground), the Cartesian equation of the trajectory is used to derive an expression for the range (R = u^2*sin(2*theta)/g). It is discovered that the optimal launch angle for maximum range is 45 degrees, where the sine of 2*theta is maximized. This conclusion is based on the assumption of no air resistance and provides a clear understanding of how the projectile's trajectory can be influenced by its launch angle.

Mindmap
Keywords
πŸ’‘Projectile Motion
Projectile motion refers to the motion of an object that is launched into the air and moves under the influence of gravity and air resistance (if considered). In the video, the motion is analyzed assuming no air resistance, focusing on the object's path, which is a parabola under these conditions. This concept is central to understanding the trajectory and range of the projectile.
πŸ’‘Trajectory
Trajectory is the path followed by an object in motion through space. In the context of the video, the trajectory is determined by the projectile's motion under the influence of gravity alone, resulting in a parabolic shape. The trajectory is of primary interest as it defines the range and maximum height the projectile can achieve.
πŸ’‘Air Resistance
Air resistance is the force that opposes the motion of an object through the air. In the video, it is initially assumed that there is no air resistance, simplifying the analysis of the projectile's motion. However, the speaker mentions that air resistance will be considered in a subsequent video, indicating its importance in real-world scenarios.
πŸ’‘Parametric Equations
Parametric equations are mathematical equations that describe the coordinates of a point moving along a curve in space. In the video, the speaker derives parametric equations for the x and y coordinates of a projectile's trajectory as functions of time, which are essential for understanding the motion of the projectile.
πŸ’‘Cartesian Equation
A Cartesian equation is an equation that describes the relationship between the x and y coordinates of points on a plane, typically in the form y = f(x). In the video, the speaker combines the parametric equations to eliminate time and derive the Cartesian equation of the projectile's trajectory, which is a key step in understanding the shape and characteristics of the path.
πŸ’‘Range
Range refers to the maximum horizontal distance an object travels in projectile motion. It is a critical parameter in understanding the effectiveness of a projectile's launch. The video provides a method to calculate the range by setting the y-coordinate of the Cartesian equation to zero and solving for the x-coordinate.
πŸ’‘Initial Speed
Initial speed is the velocity at which a projectile is launched. It is a crucial factor in determining the trajectory and range of the projectile. In the video, the initial speed is denoted by 'u' and is used in the equations for both the parametric and Cartesian descriptions of the projectile's motion.
πŸ’‘Launch Angle
The launch angle is the angle between the initial velocity vector of the projectile and the horizontal direction. It significantly influences the trajectory and range of the projectile. The video discusses the impact of the launch angle on the shape of the trajectory and the maximum achievable range.
πŸ’‘Acceleration Due to Gravity
Acceleration due to gravity is the acceleration that an object experiences due to the Earth's gravitational pull, typically denoted by 'g' and measured in meters per second squared (m/s^2). In the video, gravity acts vertically downward and affects the vertical component of the projectile's motion, influencing the y-coordinate equation and the overall trajectory.
πŸ’‘Horizontal Component
The horizontal component refers to the part of the projectile's velocity or motion that is along the horizontal direction. In the video, the horizontal component is calculated by taking the cosine of the launch angle, which indicates that there is no horizontal acceleration and the motion is uniform in the horizontal direction.
πŸ’‘Vertical Component
The vertical component is the part of the projectile's velocity or motion that is along the vertical direction. It is affected by gravity, leading to a uniformly accelerated motion. The video derives the vertical component by using the sine of the launch angle and includes it in the equation for the y-coordinate, which describes the projectile's vertical motion under gravity's influence.
Highlights

The video discusses the trajectory of a projectile without air resistance.

The aim is to find parametric equations defining the trajectory's shape.

The x-coordinate and y-coordinate as functions of time are derived.

The Cartesian equation of the trajectory is found by combining results.

The range of the projectile, its total horizontal travel, is determined.

The coordinate system origin is placed at the projectile's starting point.

The initial speed and launch angle are key parameters affecting the trajectory.

The horizontal motion has no acceleration due to lack of air resistance.

The vertical motion is influenced by gravity, leading to a constant acceleration.

The horizontal component of velocity is given by u cos theta.

The vertical component of velocity is u sine theta.

The parametric equations for x and y are derived and labeled as equations 1 and 2.

The Cartesian equation of the trajectory is a parabola, simplified using trig identities.

The range is the maximum horizontal distance the projectile travels.

The range is expressed as a function of the initial speed and launch angle.

The optimal launch angle for maximum range is 45 degrees.

The video sets up the problem and provides a foundation for future discussions on air resistance.

Transcripts

Browse More Related Video

introduction to projectile motion

NEET Physics | Projectile Motion | Theory & Problem-Solving | In English | Misostudy

Projectile Motion (of an Object Fired at an Angle) - A Level Physics

Projectile Motion: Finding the Maximum Height and the Range

Deriving the 6 Basic Projectile Motion Equations

AP Physics - Projectile Motion

Rate This

5.0 / 5 (0 votes)

Thanks for rating:

Related Tags
Projectile MotionPhysics TutorialTrajectory AnalysisLaunch AngleMotion EquationsGravity EffectsTrigonometryOptimal RangeEducational ContentScience Education