Sine & Cosine - Amplitude, Frequency & Period - [2-21-9]
TLDRThis educational video script delves into the fundamentals of sine and cosine functions, emphasizing their significance in various scientific and technological fields. It covers the concepts of amplitude, frequency, and period, illustrating how to alter these attributes to change the wave's shape and behavior. The script combines theoretical explanations with computer demonstrations to clarify how modifying the function's equation impacts its graphical representation, providing a comprehensive understanding of trigonometric wave manipulation.
Takeaways
- 📚 The lesson focuses on understanding the sine and cosine functions, their amplitude, frequency, and period, and how these concepts apply to real-life wave phenomena.
- 🌌 Sine and cosine waves are fundamental in various fields, including technology, communication, and physical theories, making their study essential for higher-level understanding.
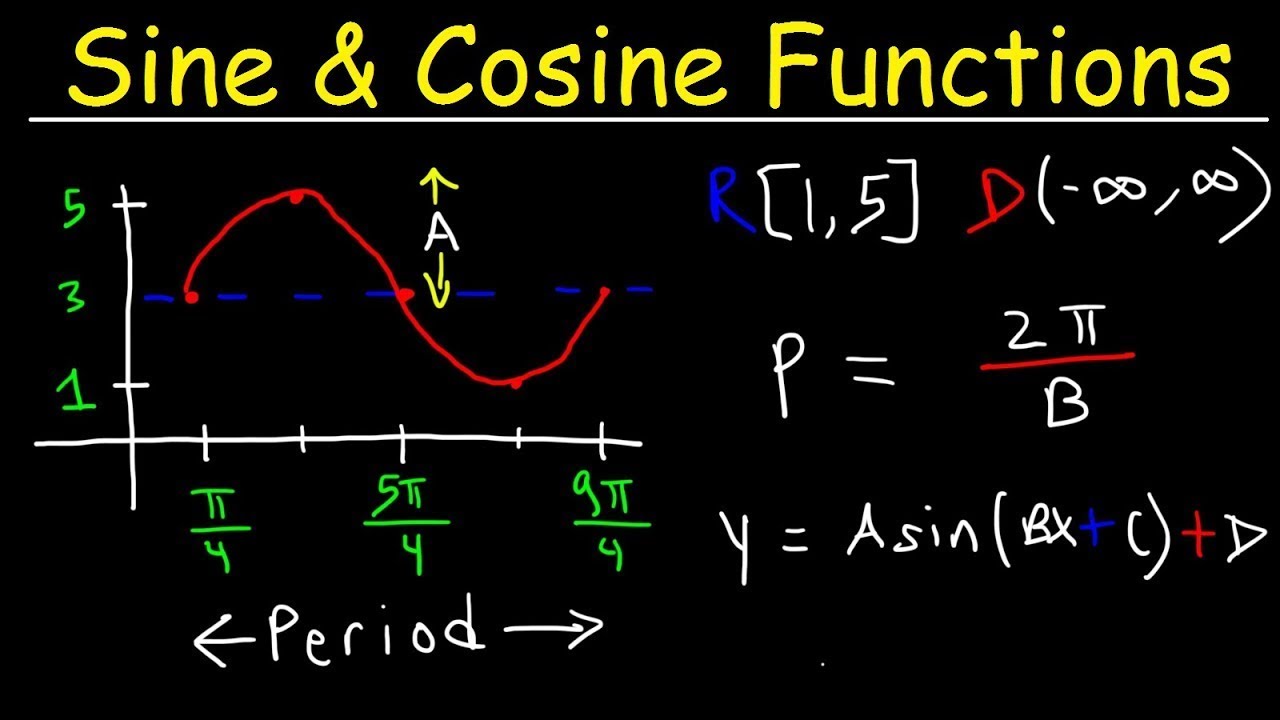
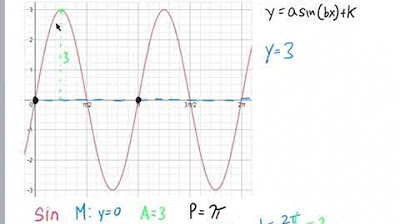
- 📈 The amplitude of a wave is its height from the x-axis to the maximum, and it can be altered to create taller or shorter waves by changing the coefficient in front of the sine or cosine function.
- 🔄 The frequency and period of a wave are related, with frequency being the number of oscillations (wiggles) per unit and the period being the time for one complete cycle; changing the number inside the sine or cosine function affects both.
- 🔀 The sine function starts at zero, reaches a maximum of one, a minimum of negative one, and returns to zero, completing one period over 2π radians, which is equivalent to one full rotation around the unit circle.
- 🔄 The cosine function starts at a maximum, goes to a minimum, and returns to its starting point, also completing one period over 2π radians, but with a phase shift of 2π/2 radians compared to sine.
- 📊 To graph sine and cosine functions with modifications, it's crucial to first understand and be able to draw the baseline functions without any modifications.
- ➕ Adding or subtracting a number to the entire sine or cosine function results in a vertical shift of the graph up or down, without changing its shape.
- ✖️ Multiplying the sine or cosine function by a number changes the amplitude of the graph, making it taller or shorter, and a negative coefficient will also invert the graph.
- 🔢 The number placed in front of 'x' in the sine or cosine function acts as a 'speed multiplier,' increasing the frequency and decreasing the period of the wave, resulting in more oscillations within the same interval.
- 📚 The formula for the new period of a modified sine or cosine function is the original period (2π) divided by the 'speed multiplier' (the number in front of 'x'), illustrating the relationship between frequency and period.
Q & A
What are the main topics covered in this lesson?
-The lesson primarily covers the sine and cosine functions, amplitude, frequency, and period of these functions, and how to graph them with different modifications.
Why are sine and cosine functions important in real life applications?
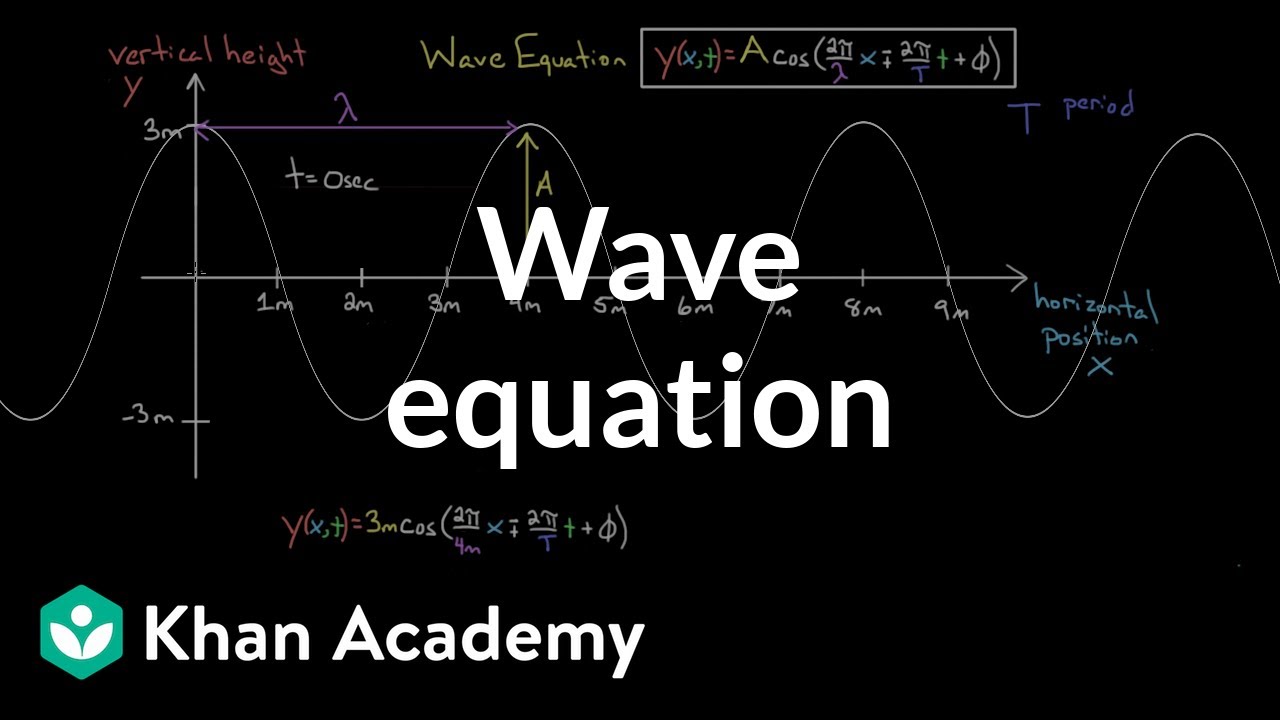
-Sine and cosine functions are important because they are fundamental to wave phenomena found in nature and technology, including radio transmissions, communication, fiber optics, wireless technologies, physical theories of gravity, and theories of matter such as electrons, protons, and photons.
What is the significance of the term 'amplitude' in the context of sine and cosine functions?
-Amplitude refers to the height of the wave from the x-axis to the top of the curve. It represents the magnitude of the oscillation in the wave, with higher amplitudes indicating larger oscillations and lower amplitudes indicating smaller oscillations.
How does the period of a sine or cosine function relate to the number of oscillations or 'wiggles' in the wave?
-The period of a sine or cosine function is the length of the x-axis over which the function completes one full cycle of oscillation. A shorter period means more oscillations or 'wiggles' in the same amount of time, indicating a higher frequency.
What happens to the graph of a sine or cosine function when a constant is added or subtracted from the function?
-When a constant is added to or subtracted from a sine or cosine function, the entire graph shifts vertically up or down by the amount of the constant, without changing the shape or period of the function.
How can the amplitude of a sine or cosine function be changed?
-The amplitude of a sine or cosine function can be changed by multiplying the function by a coefficient. A larger positive coefficient increases the amplitude, making the wave taller, while a larger negative coefficient inverts the wave and also changes the amplitude.
What is the effect of changing the number inside the sine or cosine function, such as changing from sine(x) to sine(2x)?
-Changing the number inside the sine or cosine function affects the frequency and period of the wave. A larger number inside the function increases the frequency by making the wave oscillate more times in the same period, effectively shortening the period of the wave.
How can you determine the new period of a modified sine or cosine function?
-The new period of a modified sine or cosine function can be determined by dividing the original period (2π) by the number that is in front of the variable x in the function. This factor indicates how many times the wave oscillates within the original period.
What is the relationship between frequency and period in the context of sine and cosine functions?
-Frequency and period are inversely related. A higher frequency means more oscillations in a given time, which corresponds to a shorter period. Conversely, a lower frequency means fewer oscillations in the same time, resulting in a longer period.
How does the lesson differentiate between the effects of changing the number in front of the function versus changing the number inside the function?
-Changing the number in front of the function (like in 3 * sin(x)) changes the amplitude of the wave. Changing the number inside the function (like in sin(3x)) changes the frequency and period of the wave, making it oscillate more or less frequently within the same x-axis range.
Outlines
📚 Introduction to Sine and Cosine Functions
The script begins with an introduction to the sine and cosine functions, emphasizing their importance and ubiquity in various fields such as technology, communications, and physical theories. The instructor explains the motivation behind learning these functions due to their recurring pattern in wave phenomena. The basic shape of the sine and cosine waves is reviewed, highlighting their period of 2π and their maximum and minimum values. The lesson aims to teach how to modify these basic functions to represent different wave shapes encountered in real-life scenarios.
📈 Understanding Amplitude and Period Modifications
This paragraph delves into how to alter the sine and cosine functions to change their amplitude and period. The amplitude, or the height of the wave, is discussed in the context of how it can be adjusted to create taller or shorter waves. The period, which is the time it takes for the wave to complete one full cycle, is also explained, with the instructor demonstrating how to increase the frequency of the wave by adding more 'wiggles' within the same period. The concept of frequency is introduced as the number of oscillations or cycles per unit of time.
💻 Computer Demo of Sine Wave Transformations
The instructor presents a computer demonstration to visually explain how the sine wave can be transformed. The demo illustrates shifting the wave up and down on the y-axis by adding or subtracting a constant to the sine function. It also shows how changing the amplitude is achieved by multiplying the sine function by a number. Furthermore, the effect of altering the frequency and period by adjusting the number inside the sine function (e.g., sine of 2x) is demonstrated, resulting in more oscillations within the same period.
📉 Inversion and Amplitude Adjustment of Sine Waves
This section discusses the effects of multiplying the sine function by a negative number, which not only changes the amplitude but also inverts the wave. The instructor explains that a negative multiplier effectively flips the graph, making all positive points negative and vice versa. The importance of understanding how to change the amplitude by adjusting the number in front of the sine function is reiterated, along with the visual effect of this change on the wave's appearance.
🔄 Effect of Changing the Frequency on Sine Waves
The paragraph focuses on the impact of changing the frequency of the sine wave by altering the number inside the sine function. It explains how increasing this number results in more 'wiggles' or oscillations within the same period, effectively speeding up the wave. The concept is clarified with examples, such as sine of 2x, which completes two cycles within the span of the original sine function's one cycle. The explanation helps to understand how the frequency and period are interrelated and how they can be manipulated.
📝 Transition to Practical Application and Drawing
The script transitions from theoretical discussion to practical application, emphasizing the importance of being able to draw and understand trigonometric functions. The instructor prepares to demonstrate how to apply the concepts learned from the computer demo to real-world problems. The need to internalize the baseline sine and cosine functions for reference when altering them is highlighted, as is the necessity to practice drawing these functions to solidify understanding.
🎨 Drawing and Understanding Sine and Cosine Functions
This paragraph provides a detailed guide on how to draw sine and cosine functions, emphasizing the importance of knowing the baseline functions. The instructor outlines the steps to sketch these functions, including marking key points such as the maximum and minimum values and the points where the functions cross the x-axis. The process of drawing the functions is described in a way that prepares students to modify and draw these functions when changes are applied.
✏️ Sketching Sine Functions with Vertical Shifts
The instructor demonstrates how to sketch the sine function with vertical shifts, either up or down. By adding or subtracting a constant to the sine function, the entire graph is shifted along the y-axis. The process involves drawing a new baseline and sketching the sine wave with the adjusted maximum and minimum values. The explanation includes the mathematical representation of these shifts and the visual outcome of such modifications.
🔍 Changing the Amplitude and Period of Sine Functions
This section explains how to change the amplitude and period of the sine function. The amplitude is altered by multiplying the sine function by a number, which affects the height of the wave. Changing the period, or the frequency, is achieved by adjusting the number inside the sine function, which affects how many cycles fit within the standard 2π interval. The instructor provides a formula for calculating the new period based on the original period and the scaling factor introduced by the modification.
📚 Summary of Sine and Cosine Function Transformations
The script concludes with a summary of the transformations applied to sine and cosine functions. It reiterates the effects of adding or subtracting constants for vertical shifts, multiplying by numbers to change amplitude, and adjusting the number inside the function to change frequency and period. The importance of understanding these modifications is emphasized, as they are fundamental to graphing and applying trigonometric functions in various contexts.
Mindmap
Keywords
💡Sine and Cosine Functions
💡Amplitude
💡Frequency
💡Period
💡Wave Phenomena
💡Unit Circle
💡Shifting
💡Wave Theory
💡Oscillation
💡Trigonometric Functions
Highlights
Introduction to the sine and cosine functions, emphasizing their fundamental wave shapes and applications in various fields such as technology, communication, and physical theories.
Explanation of how to graph sine and cosine functions and the importance of understanding their basic shapes before altering them.
Description of the properties of a sine wave, including its amplitude, frequency, and period, with the period of a basic sine function being 2π.
Demonstration of how to shift the sine and cosine graphs vertically by adding or subtracting a constant to the function.
Illustration of changing the amplitude of a sine wave by multiplying the sine function by a number, which affects the height of the wave.
Discussion on the effect of a negative multiplier on the sine function, which inverts the wave while maintaining the same crossing points.
Introduction to the concept of frequency and period, explaining how changing the number inside the sine function affects the wave's 'wiggling'.
Computer demo showing the graphical representation of a sine wave and how altering different components affects its shape and position.
Explanation of how to combine changes to the sine function, such as shifting, changing amplitude, and adjusting frequency, to create more complex wave forms.
Application of the same principles to the cosine function, highlighting the similarities and differences in graphing cosine compared to sine.
Tutorial on sketching sine and cosine functions by hand, emphasizing the importance of practice for understanding their properties.
Guide on how to draw and interpret the unit circle in relation to the sine and cosine functions, providing a visual aid for understanding their behavior.
Step-by-step instruction on altering the sine function to include shifts, changes in amplitude, and adjustments to the frequency or period.
Use of the formula for the period of a sine function, \( \text{Period} = \frac{2\pi}{B} \), to calculate the new period when the function is modified.
Problem-solving approach to determine the amplitude, maximum and minimum values, and period of given sine and cosine functions.
Final summary reinforcing the importance of understanding and being able to graph sine and cosine functions, and their variations.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: