Writing Equations for Sinusoidal Functions
TLDRThis educational video script guides viewers through the process of identifying and writing equations for sinusoidal graphs. It explains the difference between sine and cosine functions by their starting points on the graph. The script details how to determine the amplitude, period, and phase shift of a sine wave, using the example of a sine graph starting at the midline with an amplitude of 3 and a period of π. It also covers how to adjust the equation for a cosine graph that doesn't start at the midline, with an amplitude of 2 and a period of π, but with a phase shift. The formula for calculating the frequency (B value) is provided, and the script concludes with the equations for both sine and cosine graphs, emphasizing the importance of including the correct signs and variables.
Takeaways
- 📚 The video script is about determining the equation of a sinusoidal graph, specifically whether it is a sine or cosine graph.
- 🔍 The initial step involves identifying the type of sinusoidal function by observing where it starts from the midline.
- 📈 For sine graphs, the function starts at the midline, whereas cosine graphs start at the amplitude from the midline.
- 📉 The amplitude of the graph is determined by the distance from the midline to the highest or lowest point.
- 🔄 The period of the graph is identified by the length of one complete cycle from a starting point.
- 🌀 The general form of a sine graph equation is y = A * sin(Bx + C), where A is the amplitude, B affects the period, and C is the midline.
- 🔢 To find the value of B, which affects the period, use the formula 2π divided by the period.
- 🔄 The script explains how to determine if the graph is flipped and how to adjust the amplitude accordingly, using a negative sign.
- ✍️ The equation for the sine graph in the script is y = 3 * sin(2x), assuming no vertical shift (midline at y=0).
- 📊 The second graph is identified as a cosine graph that is flipped, starting from the bottom instead of the midline.
- 📐 The equation for the flipped cosine graph is y = -2 * cos(θ/2), with θ representing the variable and the midline at y=0.
Q & A
How can you determine whether a graph represents a sine or cosine function?
-A sine graph starts at the midline, while a cosine graph starts at the amplitude from the midline.
What is the midline in the context of the given sinusoidal graph?
-The midline is the horizontal line where the sinusoidal wave starts, which is y equals zero in the case of the sine graph described in the script.
How do you find the amplitude of a sinusoidal graph?
-The amplitude is the distance from the midline to the highest or lowest point of the wave. In the script, it is determined to be 3.
What is the period of the sine graph in the script?
-The period is the length of one complete cycle of the sine wave. In the script, it is identified as π (pi).
How do you calculate the value of B in the sine function equation?
-B is calculated by dividing 2π by the period of the wave. In the script, 2π divided by π gives B as 2.
What does the value of B represent in the sine function equation?
-B represents the factor that alters the period of the sine wave. A smaller B value results in a longer period, and a larger B value results in a shorter period.
How do you determine the direction of the sine wave (whether it is flipped or not)?
-The direction is determined by observing whether the wave starts going up or down from the midline. A positive amplitude indicates an upward start, while a negative amplitude indicates a downward start.
What is the general form of a sine function equation?
-The general form of a sine function is y = A * sin(Bx + C) + D, where A is the amplitude, B alters the period, C is the phase shift, and D is the vertical shift (midline).
What is the difference between a standard cosine graph and the one described in the script?
-A standard cosine graph starts at the maximum amplitude, while the one described in the script is flipped, starting at the minimum amplitude.
How do you find the amplitude of the cosine graph described in the script?
-The amplitude is found by measuring the distance from the midline to the highest point of the wave, which is determined to be 2 in the script.
What is the period of the cosine graph in the script?
-The period of the cosine graph is the same as the sine graph, which is π (pi), but it is adjusted by the value of B to determine the actual period of the wave.
How do you write the equation for the flipped cosine graph described in the script?
-The equation is written as y = -A * cos(Bx + C) + D, with a negative amplitude to indicate the flip, and the other values determined from the graph analysis.
Outlines
📚 Understanding Sinusoidal Graphs
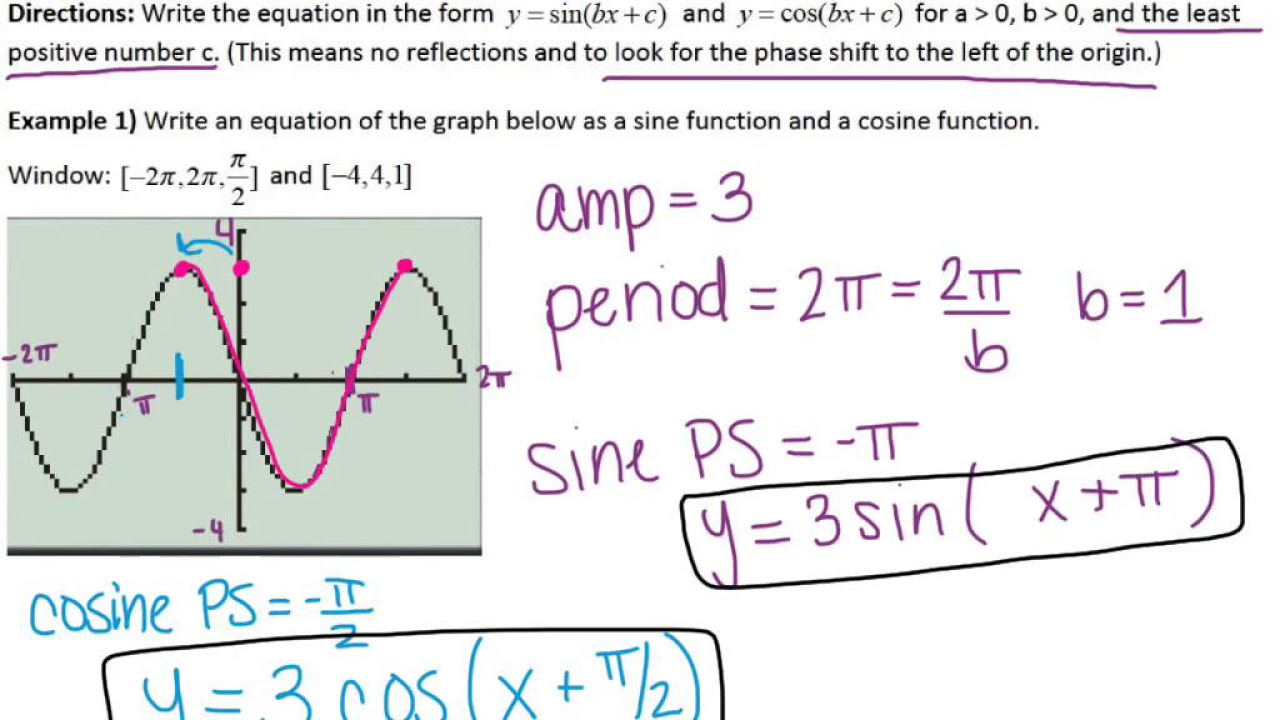
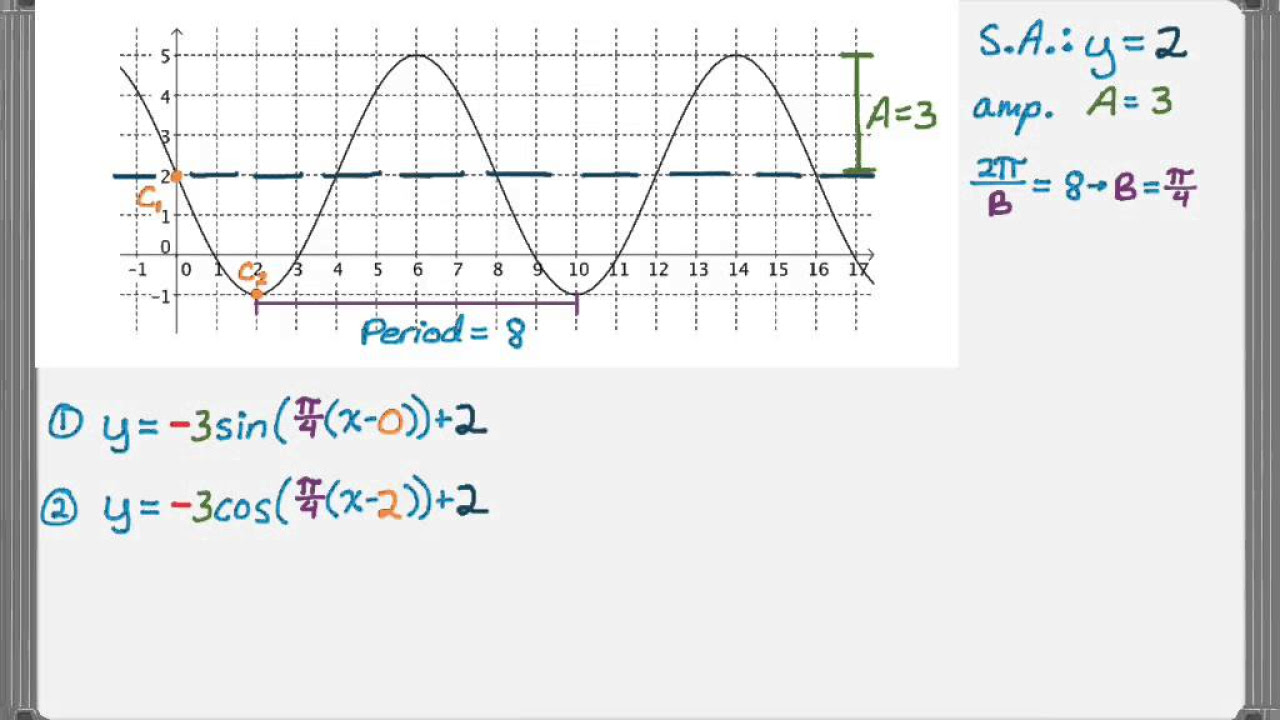
This paragraph discusses the process of identifying and writing the equation for a sinusoidal graph, specifically a sine graph. The speaker begins by determining the type of graph by observing that the sine wave starts at the midline. They establish the midline as y equals zero and identify the amplitude as 3 by measuring from the midline to the highest or lowest point. The period is determined to be π by observing the repetition of the wave. The equation for a sine graph is then written in the form y = A * sin(Bx + C) + D, where A is the amplitude, B affects the period, C is the phase shift, and D is the midline. The amplitude is confirmed as positive 3, and the period is used to calculate B, which is 2π divided by the period, resulting in B = 2. The equation is then written as y = 3 * sin(2x) + 0, with the understanding that the sine graph is not flipped.
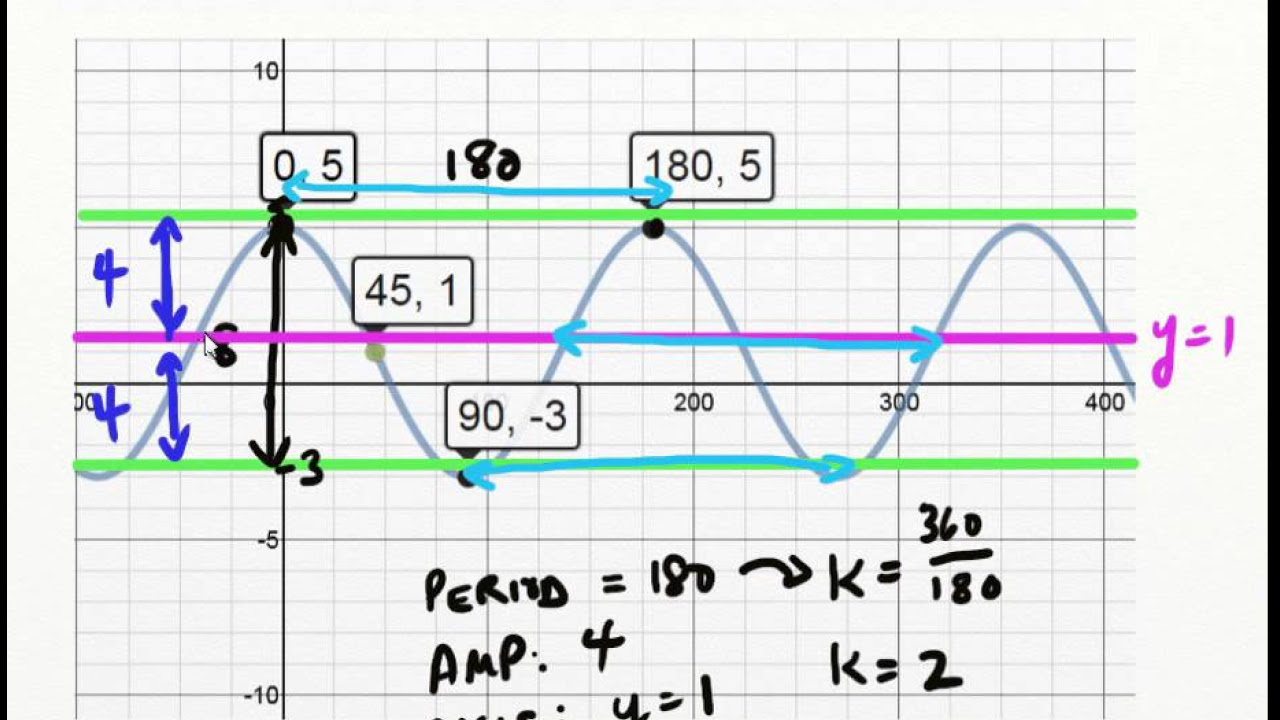
🔍 Analyzing a Flipped Cosine Graph
The second paragraph focuses on analyzing a cosine graph that has been flipped. The speaker identifies the graph as a cosine due to its starting point not being at the midline, which is the x-axis (y equals 0). The amplitude is determined to be 2, with a reminder that the graph is flipped, which will affect the equation's sign. The period is π, and using the formula for B (2π divided by the period), the value of B is found to be 1/2. The equation for the flipped cosine graph is constructed in the form y = A * cos(Bx + C) + D. The amplitude is represented as -2 to account for the flip, and the B value is 1/2. The speaker chooses to use theta instead of x and writes the final equation as y = -2 * cos(1/2 * theta) + 0, omitting the midline since it is zero.
Mindmap
Keywords
💡Sinusoidal
💡Amplitude
💡Midline
💡Period
💡Sine Function
💡Cosine Function
💡Phase Shift
💡Equation
💡Flipped Graph
💡B Value
💡Theta
Highlights
Identification of a sinusoidal graph as a sine function based on its starting point at the midline.
Explanation of amplitude determination by measuring from the midline to the highest or lowest point.
Introduction of the general sine function equation format: y = A * sin(Bx + C) + D.
Calculation of amplitude as 3 for the given sine graph.
Determination of the period of the sine wave as π (pi).
Method to find the value of B using the formula 2π/period.
Identification of the sine graph's direction based on whether it starts going up or down.
Writing the sine function equation with the amplitude, B value, and midline.
Differentiation between a sine and cosine graph based on the starting point.
Recognition that a cosine graph starts at the bottom, indicating a flipped graph.
Amplitude determination for the cosine graph as 2 with a flip.
Explanation of the cosine graph's period and how to calculate the B value.
Writing the cosine function equation with a negative amplitude to account for the flip.
Discussion on the flexibility of using X or theta in the function equation.
Final equation for the cosine graph including amplitude, B value, and midline.
Emphasis on the importance of including 'y =' or 'f(x) =' in the equation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: