Writing Equations for Trig Graphs

MrD Klinkerman

26 May 201422:45

EducationalLearning

32 Likes 10 Comments

TLDRThis educational video script focuses on determining the equations of trigonometric functions from their graphs. It explains the process of identifying key variables such as amplitude (a), vertical shift (d), period, and horizontal shift (c) for sine and cosine functions. The script provides formulas and methods to calculate these variables, including using the maximum and minimum values to find amplitude and vertical shift, and the distance between consecutive peaks or troughs to determine the period. It also covers how to ascertain the starting point for the sine and cosine cycles and the importance of the sign of 'a'. The explanation extends to the tangent function, illustrating how to find the central value, amplitude, and period by analyzing the graph's symmetry and asymptotes. The script aims to equip viewers with the skills to write trigonometric function equations from their graphical representations.

Takeaways

📚 The lesson focuses on determining the equation of a trigonometric function from its graph, specifically sine and cosine functions.
📈 To find the amplitude (|a|), calculate half the difference between the maximum and minimum values of the graph.
📉 The mid value (D) is found by averaging the maximum and minimum values, which corresponds to the vertical shift in the graph.
🔍 The period of the function can be determined by measuring the distance between two consecutive maximum or minimum values, known as peak-to-peak or trough-to-trough.
⏱ The value of B can be found using the formula |B| = 2π / period, where B affects the period of the function.
🔄 The horizontal shift is represented by the value of C, which is determined by the x-coordinate where the cycle starts for the sine function.
📊 For sine functions, the cycle typically starts at the mid value and goes to a maximum or minimum, indicating whether a is positive or negative.
📐 The value of D is the vertical shift and is equal to the sum of the maximum and minimum values divided by two.
🔢 The absolute value of a is determined by the distance from the mid value to the maximum or minimum value.
🔄 For cosine functions, the starting point can be a maximum or minimum value, which affects whether a is positive or negative.
📘 The process of finding the equation of a trigonometric function involves understanding the properties of the graph and applying specific formulas to determine the variables a, b, c, and d.

Q & A

What is the main topic of the video script?
-The main topic of the video script is determining the equation of a trigonometric function, specifically sine and cosine functions, based on the analysis of its graph.
What are the key components of a sine or cosine function that need to be determined from the graph?
-The key components that need to be determined from the graph are the amplitude (a), vertical shift (d), period (related to b), and horizontal shift (c).
How can you find the amplitude of a trigonometric function from its graph?
-The amplitude can be found by determining the difference between the highest and lowest points on the graph and then dividing that by 2. It is also the absolute value of 'a' in the function's equation.
What formula represents the relationship between the amplitude and the maximum and minimum values of the graph?
-The formula for amplitude is amplitude (or |a|) = (maximum value - minimum value) / 2.
How do you determine the vertical shift 'd' of a trigonometric function from its graph?
-The vertical shift 'd' can be determined by finding the average of the maximum and minimum values of the graph, which corresponds to the vertical shift from the midline.
What is the relationship between the period of a function and the value of 'b' in the equation?
-The relationship is given by the formula: period = 2π / |b|, which can be rearranged to find |b| as |b| = 2π / period.
How can you find the period of a sine or cosine function from its graph?
-The period can be found by measuring the distance between two consecutive maximum or minimum values, also known as peak-to-peak or trough-to-trough.
What is the significance of the value 'c' in the equation of a sine or cosine function?
-The value 'c' represents the horizontal shift of the function. It is determined by the x-coordinate where the cycle of the function begins.
How do you determine whether the value of 'a' is positive or negative for a sine function?
-For a sine function, 'a' is positive if the function goes from the mid value to a maximum value, and negative if it goes to a minimum value.
What is the process for writing the equation of a tangent function from its graph?
-The process involves determining the central value 'd', the amplitude 'a', the period (to find 'b'), and the horizontal shift 'c'. Then, these values are used to form the equation in the form y = a * tangent(b * (x - c)) + d.

Outlines

00:00

📚 Introduction to Trigonometric Function Equations

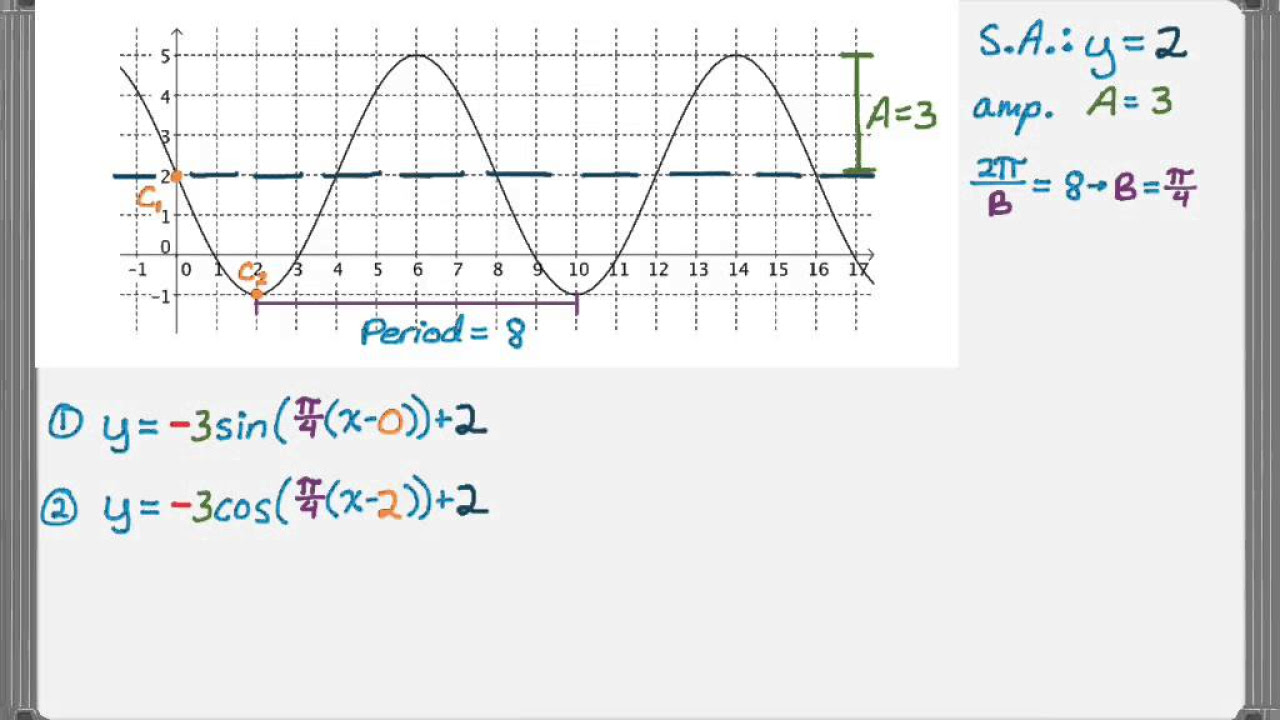
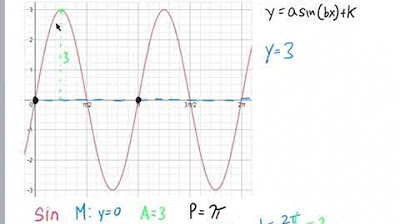
This paragraph introduces the topic of determining the equation of a trigonometric function from its graph. The focus is on understanding the sine and cosine functions and how to extract variable values such as amplitude (a), vertical shift (d), period, and horizontal shift (c) from the graph. The amplitude is calculated as half the difference between the maximum and minimum values of the function, and the vertical shift (d) is found by averaging the maximum and minimum values. The importance of examining the graph's vertical position to determine these values is emphasized.

05:01

🔍 Determining Amplitude and Vertical Shift

The speaker explains how to find the amplitude (a) and vertical shift (d) of a sine or cosine function by analyzing the graph's vertical position. The amplitude is the absolute value of 'a' and is calculated as half the difference between the highest and lowest points on the graph. To find 'd', the mid value of the graph, which is the average of the maximum and minimum values, is used. This mid value corresponds to the vertical shift in the graph. The process is illustrated with an example graph, showing how to calculate 'a' and 'd' using the maximum and minimum values.

10:01

📐 Calculating the Period and Horizontal Shift

The paragraph discusses how to determine the period and horizontal shift (c) of a trigonometric function from its graph. The period is found by measuring the distance between two consecutive maximum or minimum values, known as peak-to-peak or trough-to-trough. Once the period is known, the value of 'b' can be calculated using the formula 2π divided by the period. The horizontal shift (c) is identified by locating the x-coordinate where the cycle begins, which is the value assigned to 'c' in the function's equation.

15:01

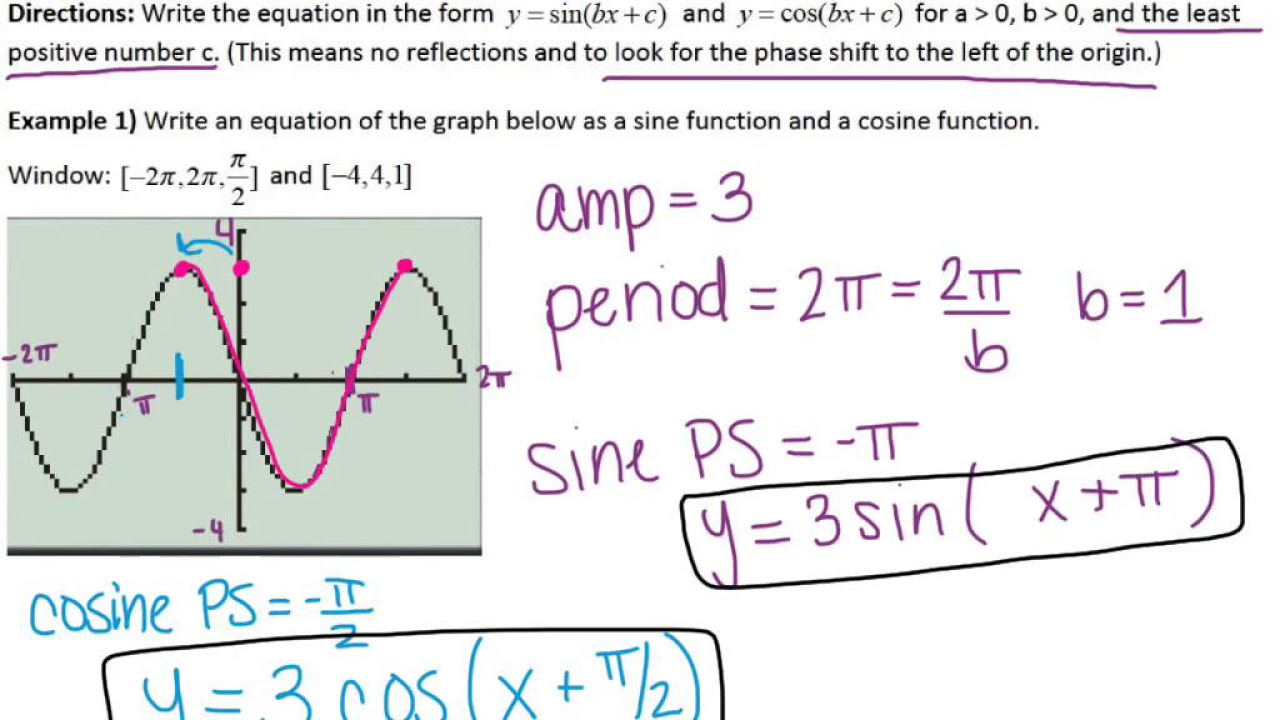
📉 Writing Equations for Sine and Cosine Functions

The speaker demonstrates how to write the equations for sine and cosine functions based on the graph's characteristics. For sine functions, the process starts with identifying the mid value and determining whether 'a' is positive or negative based on whether the function moves toward a maximum or minimum next. The cosine function's equation starts with a maximum value, indicating a positive 'a', and the horizontal shift (c) is calculated based on the x-coordinate of the maximum value. The equations are constructed using the determined values of 'a', 'b', 'c', and 'd', with examples provided for clarity.

20:01

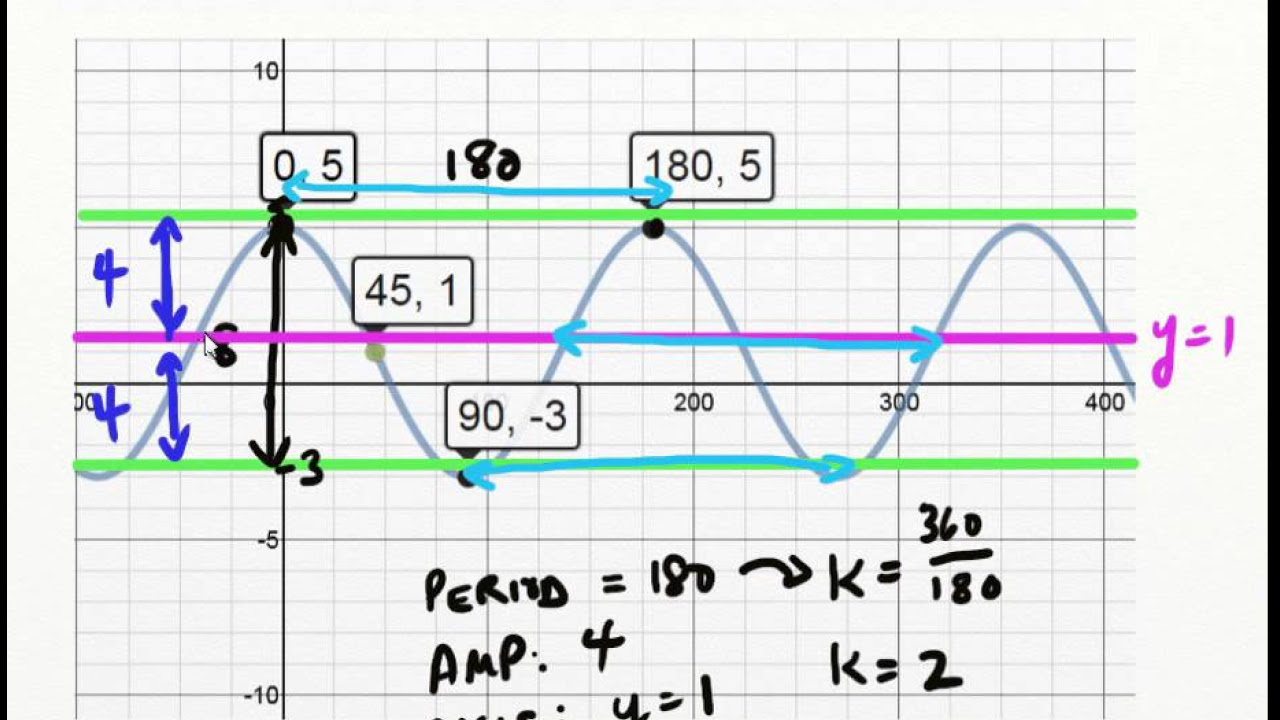
📊 Analyzing a Second Graph for Trigonometric Functions

This paragraph continues the process of analyzing a second graph to find the values of 'a', 'b', 'c', and 'd' for both sine and cosine functions. The amplitude and mid value (d) are recalculated based on the new graph's maximum and minimum values. The period is determined using the x-coordinates of two minimum values, and 'b' is calculated accordingly. The horizontal shift (c) is identified for both sine and cosine functions, and the equations are written with the new values, illustrating the process for both types of functions.

📈 Extending the Process to Tangent Functions

The final paragraph extends the process of determining trigonometric function equations to tangent graphs. Since tangent functions do not have a maximum or minimum like sine and cosine, the amplitude is not applicable. Instead, the central value (d) is identified by the point of symmetry. The amplitude (a) is determined by the distance from the mid value to the quarter and three-quarter points of the cycle. The period of the tangent function is found between the asymptotes, and 'b' is calculated using the formula π divided by the period. The horizontal shift (c) is determined by the distance of the nearest mid value from the y-axis, and the equation for the tangent function is constructed with the negative 'a', 'b', 'c', and 'd' values.

Mindmap

Keywords

💡Trigonometric function

A trigonometric function is a periodic function that relates real numbers and is defined using the angles of triangles or the unit circle. In the video, trigonometric functions are the central theme, with a focus on sine and cosine functions. The script discusses how to determine the equation of these functions by analyzing their graphs, which is a key concept in understanding the video's content.

💡Sine function

The sine function is one of the fundamental trigonometric functions that describes a smooth, periodic oscillation. It is represented as 'sin(x)' and is used to model various phenomena such as sound and light waves. In the script, the sine function is used to demonstrate how to derive its equation from a graph, including determining amplitude, period, and phase shift.

💡Cosine function

Similar to the sine function, the cosine function is another basic trigonometric function that represents a wave-like pattern. It is denoted as 'cos(x)' and is often used in conjunction with the sine function to describe more complex oscillations. The video script explains how to write the equation of a cosine function by observing its graph and identifying key characteristics.

💡Amplitude

Amplitude refers to the maximum displacement of a periodic wave from its equilibrium or mean position. In the context of the video, amplitude is used to describe the peak value of the sine or cosine function from the midline. The script explains that the amplitude can be found by taking half the difference between the maximum and minimum values on the graph.

💡Midline

The midline of a sinusoidal function is the horizontal line that passes through the middle of the wave, equidistant from the maximum and minimum values. In the video, the midline is used to determine the vertical shift (value of D) and is essential for writing the correct equation of the trigonometric function.

💡Period

The period of a function is the length of one complete cycle of the wave, often measured from one peak to the next or from one trough to the next. The script explains that the period can be determined from the graph by measuring the distance between two consecutive maximum or minimum points and is crucial for finding the value of B in the function's equation.

💡Phase shift

Phase shift, denoted by the variable C in the function's equation, refers to the horizontal displacement of the function. In the video, the phase shift is determined by looking at the x-coordinate where the function starts its cycle from the y-axis. The script demonstrates how to calculate the phase shift for both sine and cosine functions.

💡Vertical shift

Vertical shift, represented by the variable D in the function's equation, is the upward or downward movement of the entire graph of a function. The video script explains that D can be found by averaging the maximum and minimum values of the function, which helps in determining the midline.

💡Tangent function

The tangent function, written as 'tan(x)', is another trigonometric function that results in a periodic but non-smooth graph due to its vertical asymptotes. The script briefly touches on the tangent function towards the end, explaining how to determine its equation from a graph, including finding the vertical and horizontal shifts and amplitude.

💡Asymptote

An asymptote is a line that a function approaches but never intersects. In the context of the tangent function, the script mentions that the period of the tangent function can be determined by looking at the equations of its asymptotes. This is important for finding the value of B in the tangent function's equation.

Highlights

Introduction to determining the equation of a trigonometric function from its graph.

Explaining the sinusoidal curve and how to write an equation for it.

Identifying the variables a, b, c, and d in the trigonometric equation.

Focusing on the vertical position to find the amplitude (absolute value of a).

Using the formula: amplitude is half the difference between the maximum and minimum values.

Finding the mid value as the average of the maximum and minimum values.

Demonstrating the calculation of amplitude and mid value on the graph.

Discussing how to find the value of b, related to the period of the function.

Using the formula: absolute value of b equals 2π divided by the period.

Explaining how to measure the period of the function using peak-to-peak or trough-to-trough distance.

Determining the value of c (horizontal shift) for both sine and cosine functions.

Starting the sine function cycle at the nearest mid value on the y-axis.

Explaining how the direction of the first movement from the mid value determines the sign of a.

Showing how to combine the calculated values into the sine function equation.

Explaining how to find the cosine function starting from a maximum or minimum value.

Demonstrating the process with a different graph and recalculating the values.

Illustrating the same process for a tangent graph, noting differences in amplitude calculation.

Determining the period of a tangent function using the distance between asymptotes.

Concluding with the importance of understanding how to write trigonometric equations for different types of functions.

Transcripts

Browse More Related Video

Writing Sine and Cosine Equations from Graphs

Precalc 5.5 Day 2 Notes

Writing Equations for Sinusoidal Functions

MCR3U UNIT 5 Writing Sine Cosine Equation Given Graph

Trigonometry - Graphing transformations of sin and cos

Finding the equation of a periodic function from a graph or sketch

Related Tags

Trigonometry Graph Analysis Amplitude Period Horizontal Shift Sine Function Cosine Function Tangent Function Trig Equations Math Education Function Derivation