Graphing a Derivative Function | MIT 18.01SC Single Variable Calculus, Fall 2010
TLDRIn this educational video, the professor introduces a method to visualize the graph of a function's derivative from its original graph without the function's equation. The focus is on identifying horizontal tangent lines where the derivative is zero and determining the sign of the derivative across different regions of the graph. The professor illustrates how the slopes of the tangent lines correlate with the derivative's values, guiding viewers through the process of sketching the derivative's graph. The session concludes with a thought-provoking question, encouraging students to find a function whose derivative's graph mirrors the discussed example, emphasizing the impact of constants on the derivative's graph.
Takeaways
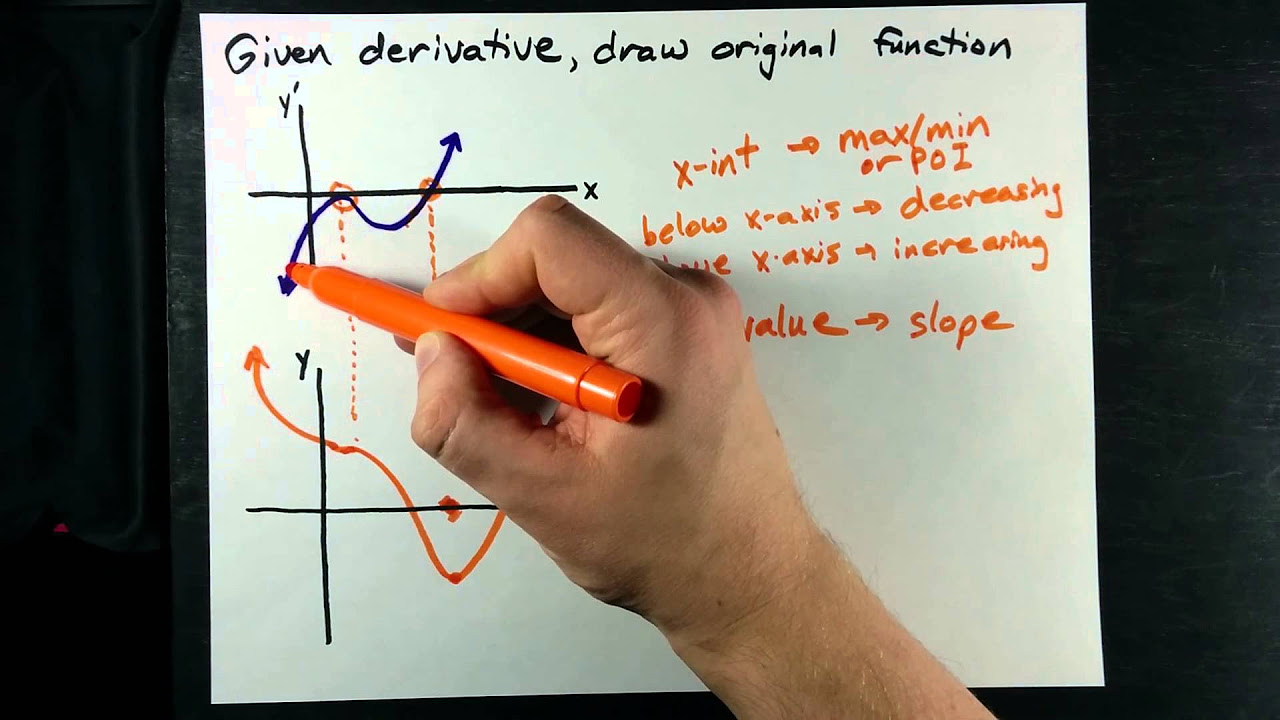
- 📚 The video aims to teach how to determine the graph of a derivative from the graph of the original function without the explicit equation.
- 🔍 The focus is on understanding the slope of the tangent line at each point on the function's graph, which the derivative represents.
- 🎯 Identifying points where the tangent line has a slope of 0 is crucial, as these are the points where the sign of the derivative can change.
- 📉 The video identifies three places where the tangent line is horizontal, indicating where the derivative is zero.
- 📈 Determining the sign of the derivative (positive or negative) in the regions between the points of zero slope helps in sketching the derivative's graph.
- 📝 The sign of the derivative (f') is recorded to the side of the graph to track its changes across different x-values.
- 📉 To the left of the first zero-slope point, the slope of the tangent line is positive, indicating f' is greater than 0.
- 📈 After the first zero-slope point, as x-values increase, the tangent lines curve downward, indicating a negative slope and thus f' is less than 0.
- 🔄 Between the two middle zero-slope points, the derivative changes from negative to zero and back to negative, showing the behavior of the slope of the tangent lines.
- 📊 The steepest slope of the tangent line corresponds to the furthest point from zero on the derivative graph, indicating the maximum magnitude of f'.
- 📚 The final graph of the derivative, f'(x), is sketched based on the behavior of the slopes and the points where the derivative is zero.
- 🤔 The challenge posed is to find a function g(x) whose derivative's graph matches the one sketched for f'(x), emphasizing that adding a constant to f(x) does not affect the slopes of the tangent lines and hence the derivative's graph.
Q & A
What is the main objective of the video?
-The main objective of the video is to demonstrate how to determine the graph of the derivative of a function from the graph of the function itself.
What does the derivative of a function represent?
-The derivative of a function represents the slope of the tangent line at each point on the graph of the function.
Why is it important to identify where the slope of the tangent line is zero?
-Identifying where the slope of the tangent line is zero is important because these points are where the derivative's value changes sign, which can affect the overall shape of the derivative's graph.
How many places does the professor identify where the tangent line has a slope of zero?
-The professor identifies three places where the tangent line has a slope of zero.
What does the sign of the derivative indicate about the function?
-The sign of the derivative indicates whether the function is increasing (positive) or decreasing (negative) at different intervals along the x-axis.
How does the professor determine the sign of the derivative in different regions of the graph?
-The professor determines the sign of the derivative by observing the slope of the tangent lines in different regions of the graph and noting whether they are positive or negative.
What is the significance of the points where the derivative is zero?
-The points where the derivative is zero are significant because they represent local maxima or minima of the function, where the slope of the tangent line is horizontal.
How does the professor suggest finding a function g(x) such that its derivative resembles the graph of f'(x)?
-The professor suggests that any function g(x) that has the same slopes as f(x) at all x-values, regardless of being shifted up or down, will have a derivative that resembles the graph of f'(x).
What is the relationship between the slopes of the tangent lines of a function and its derivative?
-The slopes of the tangent lines of a function directly correspond to the values of its derivative; the steeper the slope, the larger the magnitude of the derivative.
Why does the professor emphasize that the actual form of g(x) is not required to answer the question?
-The professor emphasizes this because the question is focused on the relationship between the graphs of the derivative and the original function, not on finding a specific algebraic expression for g(x).
How can the concept of derivatives be applied to understand the behavior of a function without its explicit equation?
-By analyzing the graph of a function, one can deduce the behavior of its derivative by observing the slopes of the tangent lines, which indicate whether the function is increasing or decreasing and where it has local maxima or minima.
Outlines
📈 Understanding Derivative Graphs from Function Graphs
The professor introduces the concept of determining the graph of a derivative function based on the graph of the original function. The focus is on identifying the slope of the tangent line at various points on the function's graph. The professor emphasizes finding points where the slope is zero, which are critical in changing the sign of the derivative. Three such points are identified on the graph. The task is to deduce the sign of the derivative between these points, noting where it's positive or negative. A visual representation of the derivative's sign is sketched below the function's graph, indicating regions of positive and negative slopes.
📊 Derivative Graph Construction and Function Relationship
This paragraph delves into plotting the derivative function, y equals f prime of x, based on the understanding of the original function's tangent slopes. The professor explains that the derivative's graph will have zeros at the points where the original function's tangent lines are horizontal. The slopes of the tangent lines indicate whether the derivative is increasing or decreasing, which helps in sketching the derivative's graph. The process involves identifying the steepest slope regions and how the slopes change from positive to negative and vice versa. The professor also poses a question to the audience, asking them to find a function g of x whose derivative's graph mirrors the one they've drawn for f prime of x.
🔍 The Relationship Between a Function and Its Derivative
The final paragraph discusses the relationship between a function and its derivative. The professor clarifies that the task is not to find an explicit form of g of x but to understand the relationship it must have with f of x to have a derivative graph that matches the one drawn for f prime of x. The key insight is that adding a constant to f of x does not affect the slopes of the tangent lines, and therefore, the derivative's graph remains unchanged. This understanding is crucial for determining a function g that, when differentiated, yields a graph identical to that of f prime of x.
Mindmap
Keywords
💡Derivative
💡Graph
💡Tangent Line
💡Slope
💡Horizontal Tangent Line
💡Sign of the Derivative
💡Magnitude of the Derivative
💡Function f(x)
💡f'(x) or f prime of x
💡Graph of a Derivative
💡Constant Function
Highlights
Introduction to the concept of determining the graph of a derivative from the graph of a function itself.
Emphasis on the derivative's role in measuring the slope of the tangent line at each point of a function.
Identification of horizontal tangent lines as points where the derivative's value is zero.
Discussion on the importance of recognizing where the slope of the tangent line is zero to understand changes in the sign of the derivative.
Graphical demonstration of three horizontal tangent lines indicating points of zero derivative.
Explanation of determining the sign of the derivative between regions of horizontal tangent lines.
Use of a sign chart to track the signs of the derivative across different x-values.
Analysis of the slope of the tangent line to infer the sign of the derivative in various regions of the graph.
Identification of regions where the derivative is positive or negative based on the slope of the tangent line.
Visual representation of how the derivative's sign changes at the zeros of the derivative.
Illustration of the process of plotting the derivative's graph based on the slope of the tangent lines.
Description of how the magnitude of the derivative corresponds to the steepness of the tangent lines.
Explanation of how the derivative's graph changes from positive to negative and back to positive as the slope of the tangent lines changes.
Demonstration of the process of sketching the derivative's graph with estimated changes in slope.
Highlighting the importance of understanding the relationship between the steepness of the tangent line and the magnitude of the derivative.
Final visualization of the derivative's graph with annotations for the regions of positive, negative, and zero values.
Challenge posed to find a function g(x) whose derivative's graph matches the derived f'(x) graph, without specifying the exact form of g(x).
Conclusion that adding a constant to f(x) does not affect the slopes of the tangent lines, hence the derivative's graph remains the same.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: