Tensor Calculus 4g: Index Juggling
TLDRThe video script delves into the concept of index juggling in tensor calculus, a fundamental yet intricate process allowing the transformation between covariant and contravariant forms. It illustrates how tensors can be manipulated by contracting with metric tensors, effectively 'juggling' indices to denote related but distinct quantities. The script clarifies the inverse operations of raising and lowering indices, and their significance in various mathematical expressions and physical laws, such as in continuum mechanics and fluid dynamics. The presentation aims to simplify the complex, making tensor calculus more approachable and emphasizing the utility of index juggling in simplifying equations across different coordinate systems.
Takeaways
- 🧩 Index juggling is a fundamental concept in differential geometry, allowing for the raising and lowering of indices in tensor expressions.
- 🔄 The process of index juggling involves contracting tensors with the covariant and contravariant metric tensors to switch between different representations of the same physical quantity.
- 📏 The covariant basis and contravariant basis are closely related and can be interconverted through index juggling, which simplifies notation and calculations.
- 🔑 The metric tensor plays a crucial role in index juggling, acting as the 'glue' that allows for the transformation between covariant and contravariant components.
- 🔄 Raising an index involves contracting with the contravariant metric tensor, while lowering an index involves contracting with the covariant metric tensor.
- 📚 The script provides an example of how to use index juggling to simplify expressions involving the inner product of vectors, making them appear as if the basis is orthonormal.
- 📉 The concept of index juggling is not just a mathematical convenience; it also has physical implications, such as in the conservation laws of continuum mechanics.
- 📝 The script explains that the Kronecker delta (\(\delta_{ik}\)) and the metric tensor are essentially the same object when viewed through the lens of index juggling, differing only in the placement of indices.
- 🔍 The importance of order is highlighted when performing index juggling, especially when dealing with non-symmetric tensors or when differentiation is involved.
- 🚫 The script warns against the common mistake of automatically applying index juggling without considering the context, such as the presence of differentiation.
- 🛠 The use of covariant and contravariant bases provides flexibility in mathematical formulations, allowing for the choice of the most convenient basis depending on the situation.
Q & A
What is index juggling in the context of the provided transcript?
-Index juggling refers to the process of moving indices up and down on tensors and other mathematical objects, which is a way to denote contractions with the covariant and contravariant metric tensors. It simplifies notation and helps to express the relationship between different components of a tensor.
Why is index juggling potentially confusing?
-Index juggling can be confusing because it involves using the same letter to denote different but closely related components of a tensor, which might initially seem counterintuitive. However, it becomes a powerful tool for simplifying expressions and understanding the relationships between different tensor components.
What is the difference between lowering and raising an index?
-Lowering an index involves contracting a tensor with a covariant metric tensor, while raising an index involves contracting with a contravariant metric tensor. These operations are inverses of each other and allow for the transformation between covariant and contravariant components of a tensor.
How does index juggling relate to the metric tensor?
-Index juggling is closely related to the metric tensor because it involves contractions with the metric tensor to transform between covariant and contravariant components. The metric tensor plays a key role in this process, as it defines how indices are raised or lowered.
What is the significance of using the same letter for different but related tensor components?
-Using the same letter for different but related tensor components, as in index juggling, helps to emphasize the close relationship between these components. It also simplifies notation and makes it easier to work with tensors in various mathematical expressions.
How can index juggling be used to simplify expressions involving inner products of vectors?
-Index juggling can simplify expressions involving inner products of vectors by allowing the use of a single letter to denote both covariant and contravariant components. This leads to more compact expressions that can be easily manipulated and understood.
What is the role of the Kronecker delta (Δ) in index juggling?
-The Kronecker delta (Δ) is used in index juggling to represent the metric tensor when indices are lowered. It is an alternative notation that can be used to denote the metric tensor, especially in cases where the metric tensor is represented by a matrix of ones and zeros.
Can index juggling be applied to tensor identities?
-Yes, index juggling can be applied to tensor identities. It allows for the transformation of tensor identities by raising or lowering indices, which can be useful for simplifying complex expressions or deriving new relationships.
Why is it important to keep track of the order of indices when lowering or raising them?
-Keeping track of the order of indices is important because the operations of lowering and raising indices involve contractions with metric tensors, which can be sensitive to the order of indices. However, for symmetric tensors like the Kronecker delta, the order does not matter.
How does index juggling affect the appearance of mathematical expressions involving tensors?
-Index juggling can make mathematical expressions involving tensors appear simpler, as it allows for the use of fewer indices and more compact notation. However, it is important to remember that the simplicity is superficial, as the actual calculations still involve the metric tensor.
What are the practical implications of index juggling in fields like continuum mechanics?
-In fields like continuum mechanics, index juggling can simplify the formulation of equations, especially when dealing with covariant and contravariant coordinates. It allows for the transformation of equations into more convenient forms, which can be easier to solve or analyze.
Outlines
🧩 Index Juggling in Tensor Notation
This paragraph introduces the concept of index juggling in the context of tensor notation. It explains how contracting a tensor with a covariant basis results in a new set of numbers that are closely related to the original set, warranting the same letter notation but with a different position for the index. The process of 'lowering' and 'raising' indices is described, demonstrating how these operations are inverses of each other and how they allow for the recovery of original values through metric tensor contraction. The paragraph also illustrates the practicality of this notation in simplifying expressions and maintaining relationships between mathematical objects.
📚 Practical Examples of Index Juggling
The second paragraph delves into practical examples of index juggling, showing how it simplifies the notation of tensor operations. It discusses the decomposition of a vector with respect to both covariant and contravariant basis, and how these decompositions are related through index juggling. The concept is further clarified through the definition of the contravariant basis, which is shown to be a special case of index juggling. The paragraph emphasizes the visual appeal and compactness of expressions made possible by this notation, as well as its utility in differentiating between covariant and contravariant components of vectors.
🔍 Orthonormal Basis and Metric Tensor Clarifications
This paragraph explores the implications of index juggling in the context of orthonormal and non-orthonormal bases, highlighting the role of the metric tensor in the latter case. It discusses how the index juggling convention simplifies expressions to appear as if the basis is orthonormal, even when it is not. The paragraph also addresses potential confusion regarding the placement of indices and the importance of order in tensor expressions. It provides an abstract example of how to manipulate expressions with raised and lowered indices, emphasizing the need to understand the underlying tensor identities and the role of the metric tensor in these operations.
🔗 The Metric Tensor and Index Juggling
The fourth paragraph focuses on the metric tensor and its relationship with the Kronecker delta through index juggling. It explains how lowering an index on the metric tensor can be represented using the Kronecker delta and vice versa, illustrating the equivalence between the two. The paragraph also discusses the potential for confusion when interpreting these notations, especially in different coordinate systems, and emphasizes the importance of understanding the underlying tensor operations. It concludes with a note on the utility of index juggling in simplifying tensor expressions and equations.
🛠 The Utility of Covariant and Contravariant Basis
This paragraph discusses the reasons for having both covariant and contravariant bases, emphasizing their mathematical utility and practical applications in fields like continuum mechanics. It explains how these bases allow for the writing of equations in a simplified form and how index juggling facilitates the transition between the two. The paragraph also touches on the conservation of vorticity in fluid dynamics as an example where the choice of basis can affect the complexity of the equations. It concludes by highlighting the importance of understanding the index juggling convention to avoid mistakes in tensor operations.
🔄 The Dual Nature of Tensor Operations
The final paragraph reinforces the dual nature of tensor operations, emphasizing the importance of choosing the right basis for a given problem. It discusses how having both covariant and contravariant bases provides flexibility in mathematical expressions and problem-solving. The paragraph also touches on the simplification of tensor products through index juggling and the ease with which these operations can become second nature to practitioners. It concludes by reiterating the importance of understanding the underlying principles of tensor notation and the role of index juggling in facilitating these operations.
Mindmap
Keywords
💡Index Juggling
💡Covariant Basis
💡Contravariant Basis
💡Metric Tensor
💡Raising and Lowering Indices
💡Tensor
💡Orthonormal Basis
💡Differentiation
💡Continuum Mechanics
💡Vorticity
Highlights
Index juggling is a fundamental concept in differential geometry, allowing for the transformation between covariant and contravariant tensors.
The process of index juggling can be confusing due to its simplicity, but it is essential for working with tensors that are not necessarily simple.
Contraction with the covariant metric tensor results in a new set of numbers that are closely related to the original, denoted by the same letter.
Index juggling is used to denote contractions with the covariant metric tensor and is also applicable in reverse for contravariant tensors.
The operations of lowering and raising indices are inverses of each other, simplifying the notation and understanding of tensor relationships.
Index juggling allows for the recovery of original tensor values through contraction with the contravariant metric tensor.
The concept of index juggling is demonstrated through the abstraction of tensor operations, showing its broad applicability.
The order of indices is crucial in tensor operations, especially when lowering or raising indices in tensor expressions.
The transcript explains how to denote tensors with lowered indices, emphasizing the importance of tracking index positions.
Examples of index juggling are provided, including the decomposition of vectors with respect to covariant and contravariant bases.
The relationship between covariant and contravariant components of a vector is shown to be interconnected through index juggling.
The transcript clarifies the surprising use of the same letter for covariant and contravariant bases as a special case of index juggling.
Index juggling simplifies expressions, making them appear as if the basis is orthonormal, even when it is not.
The transcript discusses the limitations of index juggling, particularly when dealing with derivatives and the contravariant tensor.
The concept of tensor identity and its manipulation through index juggling is explored, including the lowering of live indices.
The transcript explains the equivalence between the Kronecker delta and the metric tensor when indices are lowered or raised.
The importance of understanding the metric tensor's role in index juggling, especially in non-Cartesian coordinate systems, is highlighted.
The transcript concludes by emphasizing the practical utility of index juggling in simplifying mathematical expressions and equations in various coordinate systems.
Transcripts
Browse More Related Video

Video 22 - Raising & Lowering Indexes

Tensors for Beginners 16: Raising/Lowering Indexes (with motivation, sharp + flat operators)
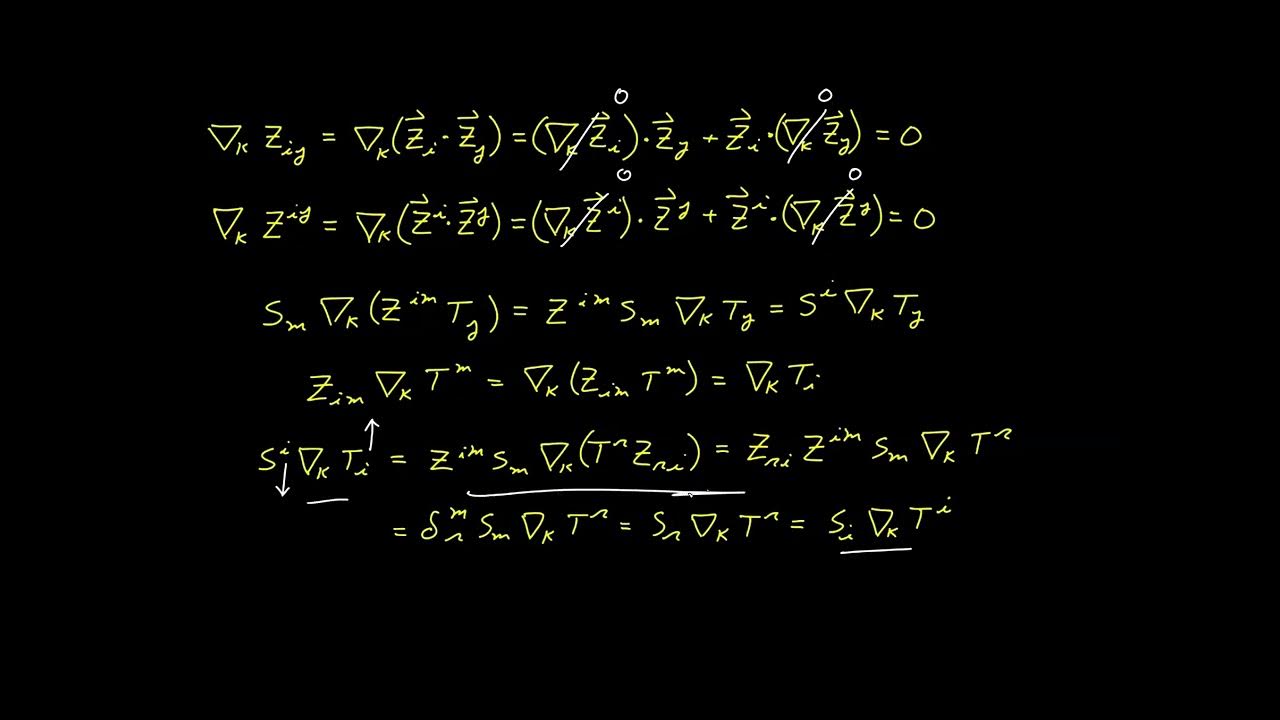
Video 38 - Metrinilic Property - Part 2

Tensor Calculus 4c: A Few Tensor Notation Exercises

Tensor Operations: Contractions, Inner Products, Outer Products

Tensor Calculus Lecture 7b: Relative Tensors
5.0 / 5 (0 votes)
Thanks for rating: