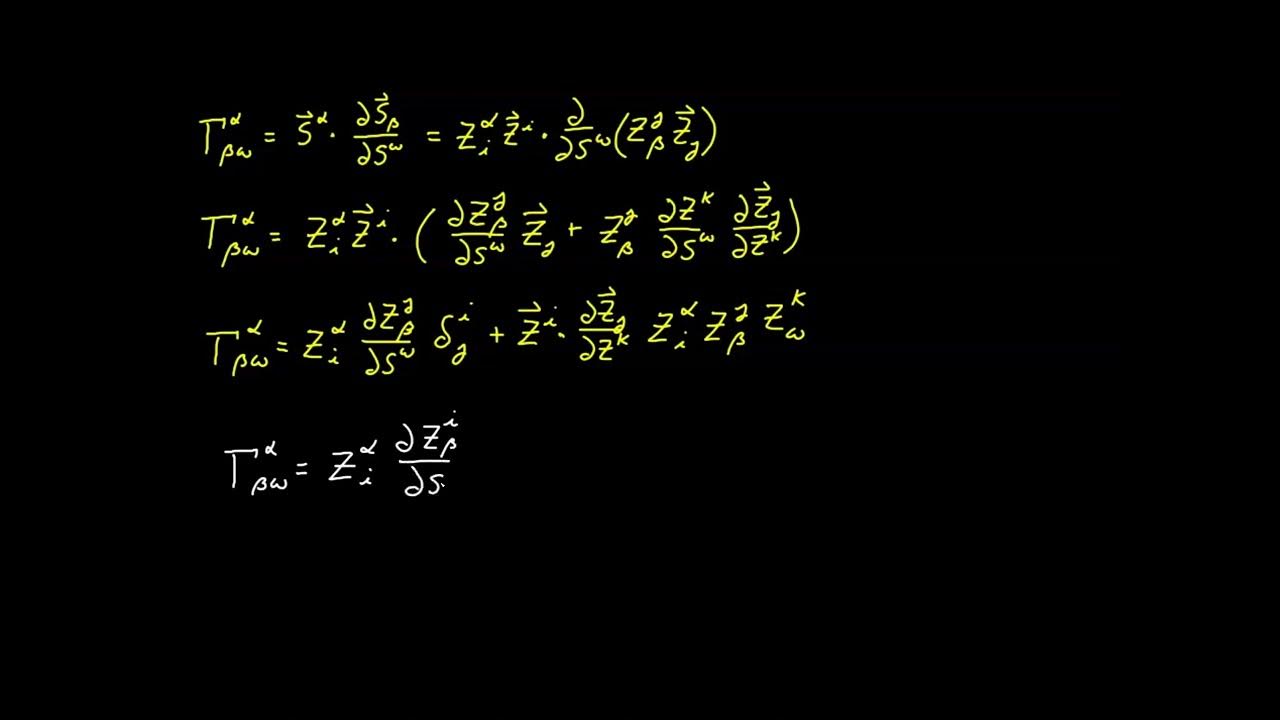Tensor Calculus 8d: The Christoffel Symbol on the Sphere of Radius R
TLDRIn this educational script, the presenter delves into the computation of Christoffel symbols on a sphere of radius R, transitioning from discussing curvature to the intricacies of these symbols. The explanation involves the contravariant basis vectors and their relationship with the metric tensor, leading to the identification of non-zero Christoffel symbols. The process is enriched with visualization exercises, emphasizing the importance of understanding the geometric and algebraic properties of the sphere's surface.
Takeaways
- 📚 The lecture discusses the computation of the Christoffel symbols on a sphere of radius R, transitioning from a curvature tester to the Christoffel symbol computation.
- 🔍 The Christoffel symbols are defined by their relationship with the covariant and contravariant basis vectors, which are key to understanding their computation on the sphere.
- 📐 The contravariant basis vectors have lengths that are adjusted based on the metric tensor, pointing in the same direction but with lengths of 1/R for s1 and 1/(R * sin(theta)) for s2.
- 🌐 The computation involves considering the rate of change of these basis vectors with respect to the spherical coordinates theta and phi, which is essential for determining the non-zero Christoffel symbols.
- 📈 The derivative of the basis vector s1 with respect to theta points inward, normal to the tangent plane, leading to certain Christoffel symbols being zero due to orthogonality.
- 🔄 The symmetry of the Christoffel symbols, specifically gamma_12 being equal to gamma_21, is highlighted, a property that is always mentioned but not derived in the script.
- 📝 The first two non-zero entries of the Christoffel symbols are identified as gamma_12 and gamma_21, both equal to cotangent(theta), which is a significant result from the computation.
- 🤔 The script encourages the audience to visualize the changing vectors and their derivatives, emphasizing the importance of spatial understanding in differential geometry.
- 🧭 The computation of gamma_22 is approached by considering the derivative of the basis vector s2 with respect to phi, leading to the conclusion that gamma_22 is zero due to orthogonality.
- 📉 The final non-zero Christoffel symbol, gamma_11, is computed by considering the dot product of the derivative of s1 with s1, resulting in a value of -sine(theta) * cosine(theta).
- 🔗 The script concludes by noting that none of the computed Christoffel symbols depend on the radius R, which is an important observation for the properties of the sphere.
Q & A
What is the Christoffel symbol used for in the context of the script?
-The Christoffel symbol is used to compute the rate of change of basis vectors on a sphere of radius R, which is crucial for understanding the curvature and geometry of the sphere.
What is the significance of the contravariant basis vectors in this context?
-The contravariant basis vectors are important because they point in the same direction as the covariant basis vectors, but their lengths are scaled differently, affecting the computation of the Christoffel symbols.
How does the length of the contravariant vector s1 relate to the radius R?
-The length of the contravariant vector s1 is 1 over R, indicating that it is scaled inversely with respect to the radius of the sphere.
What is the relationship between the derivative of s1 with respect to theta and the normal to the tangent plane?
-The derivative of s1 with respect to theta points in the direction normal to s1 and is orthogonal to the tangent plane, which is a key aspect in determining the Christoffel symbols.
Why are the values of gamma_11 and gamma_22 zero?
-The values of gamma_11 and gamma_22 are zero because the derivative of s1 with respect to theta and the derivative of s2 with respect to theta are orthogonal to the tangent plane, resulting in a dot product of zero.
What is the symmetry property of the Christoffel symbols mentioned in the script?
-The Christoffel symbols have a symmetry property where gamma_12 is equal to gamma_21. This is an important property that simplifies the computation and understanding of the symbols.
What is the formula for the nonzero entry of gamma_12 and gamma_21 in terms of theta?
-The nonzero entry for gamma_12 and gamma_21 is given by the cotangent of theta, which is a result of the dot product between the derivative of s1 with respect to phi and s2.
How does the derivative of s2 with respect to phi affect the computation of gamma_22?
-The derivative of s2 with respect to phi is orthogonal to s2, which means that the dot product used to compute gamma_22 will be zero, making gamma_22 equal to zero.
What is the significance of the angle between the derivative of s1 with respect to phi and s2 in computing gamma_12?
-The angle between the derivative of s1 with respect to phi and s2 is pi minus theta, which is used to compute the cosine of the angle for the dot product in the formula of gamma_12.
Why is it important to visualize the vectors and their derivatives when computing the Christoffel symbols?
-Visualization is crucial in understanding the geometric relationships between the vectors and their derivatives, which helps in correctly applying the formulas and interpreting the results of the Christoffel symbols.
How does the script suggest verifying the independence of the computed Christoffel symbols from the radius R?
-The script suggests reviewing the calculations and ensuring that the computed values do not have R as a factor, which would indicate dependence on the radius.
Outlines
📚 Introduction to Christoffel Symbols on a Sphere
The speaker begins by discussing the transition from using a curvature tester to calculating the Christoffel symbols on a sphere of radius R. They emphasize the importance of understanding the contravariant basis vectors and their relationship with the covariant basis, especially in the context of the contravariant metric tensor. The speaker introduces the formula for the Christoffel symbols and explains that these quantities can no longer be interpreted as the components of four vectors with respect to the covariant basis. They provide a detailed explanation of how the contravariant basis vectors point in the same direction but have different lengths, dependent on the radius or its reciprocal squared. The speaker then starts to compute the non-zero Christoffel symbols, specifically focusing on gamma 1 1 s gamma, and explains the process of finding the rate of change of the vector with respect to theta.
🔍 Calculating Non-Zero Christoffel Symbols for a Sphere
In this paragraph, the speaker delves deeper into the computation of the non-zero Christoffel symbols for a sphere. They discuss the symmetry of the symbols and the importance of visualizing the vectors involved. The focus is on calculating gamma 1 2 and gamma 2 1, which are found to be equal due to symmetry. The speaker uses the contravariant basis vector to explain the changes in the vector as a function of theta and phi, highlighting the orthogonality of the derivative to the tangent plane. They also discuss the visualization of the derivative of the vector s1 with respect to phi, pointing out that it will be orthogonal to s1 and s2, leading to a non-zero entry for gamma 1 2 and gamma 2 1. The speaker concludes with the values of these non-zero Christoffel symbols, which are related to the cotangent of theta.
🌐 Finalizing Christoffel Symbols and Reflecting on Symmetry
The speaker concludes the discussion on the Christoffel symbols for a sphere by addressing the remaining combination, gamma 2 2. They use the dot product of gamma with the derivative of s2 with respect to phi to find that gamma 2 2 is zero, which is consistent with the orthogonality of the vectors involved. The speaker also reflects on the symmetry of the Christoffel symbols with respect to the lower indices, despite the expressions not appearing symmetric. They encourage the audience to consider the symmetry by visualizing the derivative of s2 with respect to theta and how it would yield the same result due to the inherent symmetry of the problem. The speaker wraps up by summarizing the Christoffel symbols for the sphere, which are functions of the standard spherical angles theta and phi, and expresses hope for the correctness of the calculations.
Mindmap
Keywords
💡Christoffel symbol
💡Curvature tensor
💡Contravariant basis vector
💡Covariant basis vector
💡Metric tensor
💡Spherical coordinates
💡Derivative
💡Symmetry
💡Tangent plane
💡Orthogonal
💡Visualization
Highlights
Introduction to computing the Christoffel symbol on a sphere of radius R.
Switching from curvature tester to Christoffel symbol computation.
Explanation of the formula for Christoffel symbols and their definition.
Clarification on the interpretation of Christoffel symbols with respect to contravariant and covariant basis vectors.
Description of the contravariant metric tensor and its implications on basis vector lengths.
Starting computation of gamma 1 1 s gamma and its relation to the rate of change of the vector with respect to theta.
Documentation of non-zero Christoffel symbols and their significance.
Vector s 1 described as a vector of length R rotating uniformly.
Derivative of s 1 pointing inward with a length related to the curvature tensor.
Zero values for certain Christoffel symbols due to orthogonality with the tangent plane.
Computation of gamma 1 2, salmon, and its symmetry with gamma 2 1.
Visualizing the change of vector s 2 with respect to theta and its implications.
Derivative of s 1 with respect to phi and its orthogonality to s 1.
Calculation of gamma 1 2 and gamma 2 1 with the result in terms of cotangent theta.
Exploration of gamma 2 2 and its orthogonality to s 2 leading to a zero value.
Final computation of gamma 1 2 in terms of sine and cosine theta.
Review of the symmetry of Christoffel symbols with respect to lower indices.
Conclusion of the Christoffel symbols for a sphere with standard spherical angles theta and phi.
Encouragement for the audience to visualize and understand the forces involved in the computation.
Transcripts
5.0 / 5 (0 votes)
Thanks for rating: